离散设计空间中的最优解

由于离散设计空间的不连续性，离散变量最优点与连续变量最优点不是同一概念，必须重新定义。

1.离散单位邻域

在设计空间中，离散点X的单位邻域UN（X）是指如下式定义的集合：

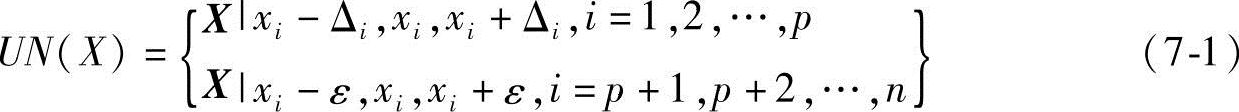
图7-3所示为二维设计空间中离散点X的离散单位领域，则

UN（X）=｛A，B，C，D，E，F，G，H，X｝

一般情况下，设离散变量的维数为P，则UN（X）内的离散点总数为N=3^P。

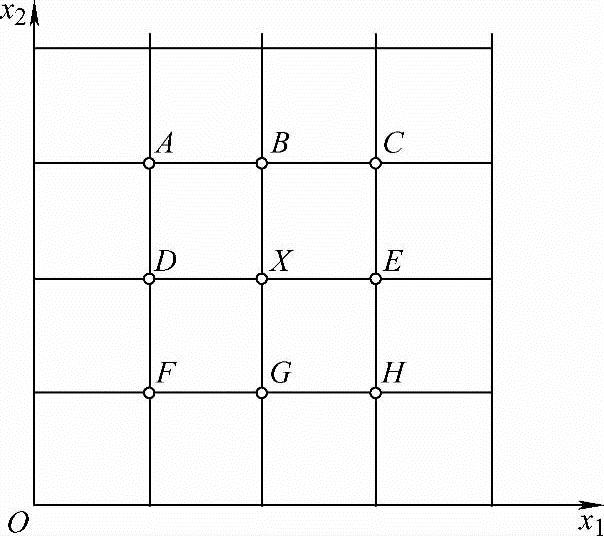
图7-3 二维设计空间中离散点的离散单位邻域

2.离散坐标邻域

在设计空间中离散点X的离散坐标邻域UC（X）是指以X点为原点的坐标轴线和离散单位邻域UN（X）的交点的集合。在图7-3中，离散点X的离散坐标邻域为(www.xing528.com)

UC（X）=｛B，D，E，G，X｝

一般在P维离散变量情况下，离散坐标邻域的离散点总数为N=2P+1。

3.离散局部最优解

若X^*∈D，对所有X∈UN（X^*）∩D，恒有f（X^*）≤f（X），则称X^*是离散局部最优点。

4.拟离散局部最优解

若，巨对所有X∈UC（X^*）∩D，恒有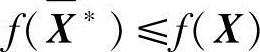，则称X^*是拟离散局部最优点。

5.离散全域最优解

若X^**∈D，且对所有X∈D，恒有f（X^**）≤f（X），则称X^**为离散全域最优点。

严格说来，离散优化问题的最优解是针对离散全域最优点而言，但它与一般的非线性优化问题一样，离散优化方法所求得的最优点一般是局部最优点，这样通常所说的最优解均指局部最优解。

由于设计空间的离散性，离散最优点将不是唯一的。为了判断X点是否是最优点，应将UN（X）内所有离散点迸行比较，得到局部最优点X^**。但由于在UN（X）中离散点的总数目N=3^P，若维数P很大，则判断离散局部最优点X^**的计算工作量太大，故也可仅在UC（X）中迸行比较，UC（X）的离散点总数仅有2p+1个，计算工作量相对来说少一些。但这样判断得到的是拟离散局部最优点，它可能是离散局部最优点，也可能不是，因而以此作为离散最优点，其可靠程度会低一些。