设计实例：多目标函数优化法优化

例6-1 试用线性组合统一目标函数法优化蟹爪式装载机抓取机构。图6-5表示该机器的外形图和计算简图。这个工作机构是属曲柄直线导轨机构，对它的设计要求是：

1）曲柄直线导轨机构M点的轨迹（x_Mj，y_Mj）与给定的轨迹曲线（x_0j，y_0j）的误差达到最小，即

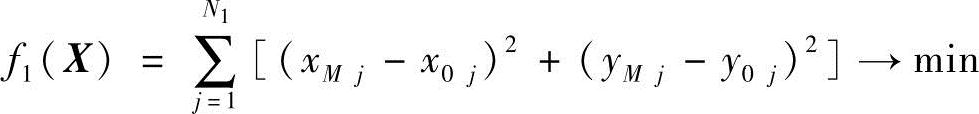
2）抓取机构抓爪的位置角α_j与给定的位置角α_0j的误差为最小，即

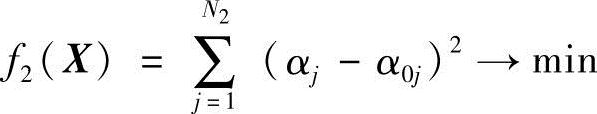
3）要求曲柄的位置角φ与预期轨迹曲线上指定点相对应，即当曲柄在φ₁位置时连杆点φ₁对应于（x₀₁，y₀₁）点，φ₂位置时对应于（x₀₂，y₀₂）点等，即应该使

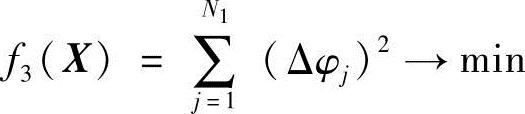
式中，N₁为所取的再现轨迹点数；N₂为所取的再现位置角点数，通常N₂＜N₁；Δφ_j为规定的曲柄间隔差值，Δφ_j=φ_j+1-φ_j。

这样，统一目标函数可按如下方法来建立：

Φ（X）=W₁f₁（X）+W₂f₂（X）+W₃f₃（X）→min

由于三个目标函数均为误差值，所以其三个加权因子W₁、W₂和W₃值可用误差容限法。取α_j=0，β_j=f_j（X^（0））（j=1，2，3），其加权因子值取W_j=1/［（β_j-α_j）/2]²（j=1，2，3）。

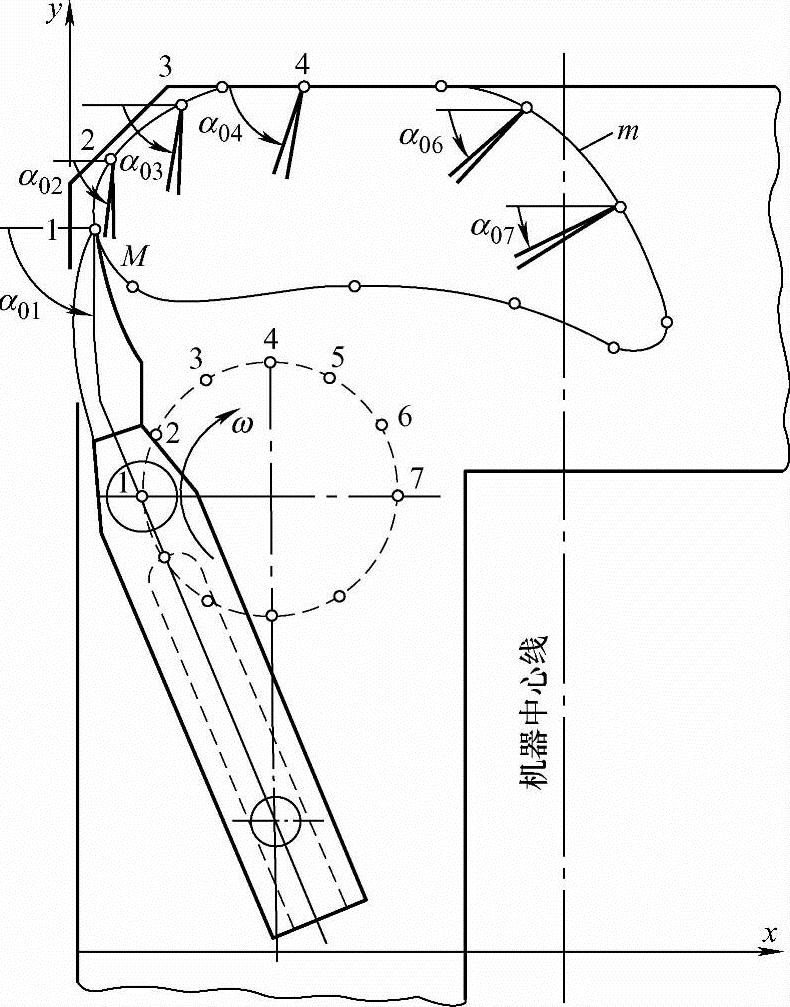
图6-5 蟹爪式装载机工作机构优化设计示例

例6-2试用协调曲线法优化恒载作用下的径向动压滑动轴承。如图6-6所示，设F为轴承的径向载荷，n为转速，c为轴承间隙（其值近似等于D₁-D），μ为润滑油的黏度。一般来说，动压轴承的工作能力和寿命主要取决于供油量Q及温升Δt。供油量若不足，就不能产生油膜；若有足够的供油量，一方面可以补充轴承泄漏的油量，另外还可以通过漏出的油带走一部分热量，不致发生过热现象。因此，从实际意义上说，应取两个设计指标，即使油膜温升Δt和润滑油流量Q达到最小。设计变量取X=（L/D，c，μ）^T，并满足0.25≤L/D≤1，h_min≥0.00127mm，p_f≥9.26MPa，μ≥0.006859Pa·s，Δt≤150°等的约束条件。

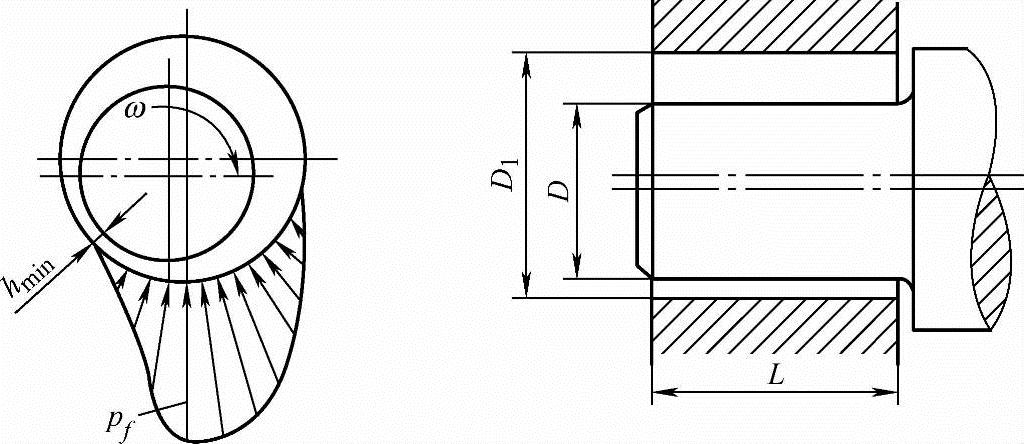
图6-6 径向动压滑动轴承

这是一个三维的两个目标函数的优化设计问题。在图6-7中画出了油流量Q与油膜温升Δt的协调曲线，它表示了满足K-T条件的所有非劣解。为了从中选出“选好解”，可以先作出当不同温升Δt时的各主要参数的变化曲线，如图6-8所示。从图中的各特性曲线可以看出，相应于S点将是一个较好的设计方案。因为在S点的左边，轴承间隙很快增加，当间隙过大时，就会晃动，运动不稳定，使在工作中产生噪声；若在S点右边，功率损失和油的黏度增加较快，这是不好的。在S点，Δt=7.5℃，所以选好解应为f₁^*（X）=Δt=7.5℃，f₂^*（X）=Q=18cm³·s^-1，设计点为X=（0.3，0.0482，0.006859）T

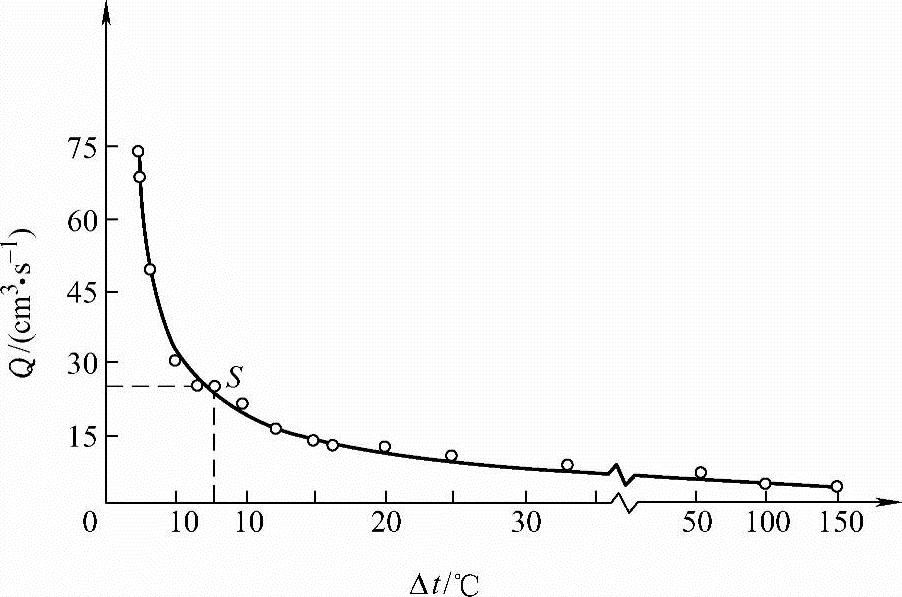
图6-7 动压滑动轴承润滑油流量与油膜温升的协调曲线

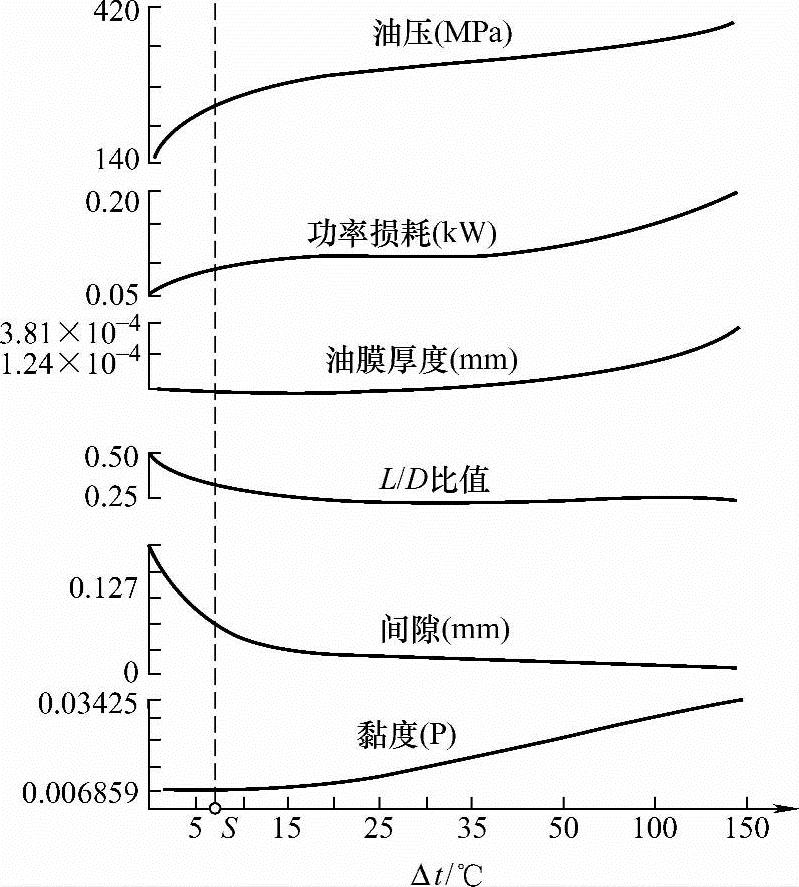
图6-8 动压滑动轴承各参数的特性曲线

注：1hp=745.700W，1P=10^-1Pa·s。

例6-3 试用功效系数法建立如图6-9所示的门座式起重机变幅四杆机构的优化设计模型。

解：这个机构的设计希望达到如下几项要求：

（1）在四杆机构变幅行程中，要求E点沿水平直线，即

f₁（X）=｛max|y-h|｝→min(www.xing528.com)

（2）在四杆机构变幅行程中，要求E点的水平分速度的变化最小，以减小货物的晃动，即

f₂（X）=｛max|Δv_x/Δα|｝→min

（3）货物对支点A所引起的倾覆力矩差要尽量小，即

f₃（X）=｛max|ΔM|｝→min

这三个目标函数都属同类性质，即目标函数值越小越好。所以可以按同一种功效系数函数来定义。例如，对于轨迹目标函数，可参照国际最先迸的设计水平，按照设计要求先定出最坏和最好的两个临界值，如图6-10所示，若|Δy|_max＜0.1m，则取d₁=1；若|Δy|_max＞0.5m，则取d₁=0；然后，再取当|Δy|_max=0.3m，d₁=0.7；|Δy|_max=0.5m，d₁=0.3。这样，把各点间用直线分段连接起来，便得到分段的线性功效系数函数d₁=f（|Δy|_max）。同样道理亦可以定义出水平适度变化率的功效系数函数d₂=f（|Δv_x/Δα|_max）和倾覆力矩差的功效系数函数d₃=f（|ΔM|_max）。

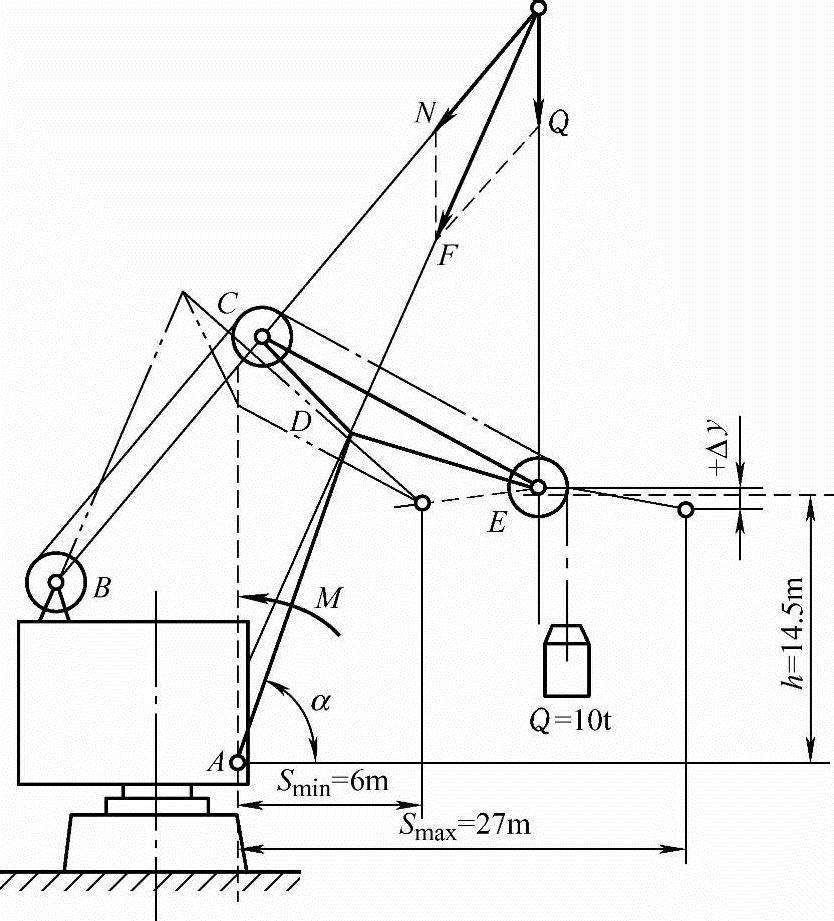
图6-9 门座式起重机变幅四杆机构的计算简图

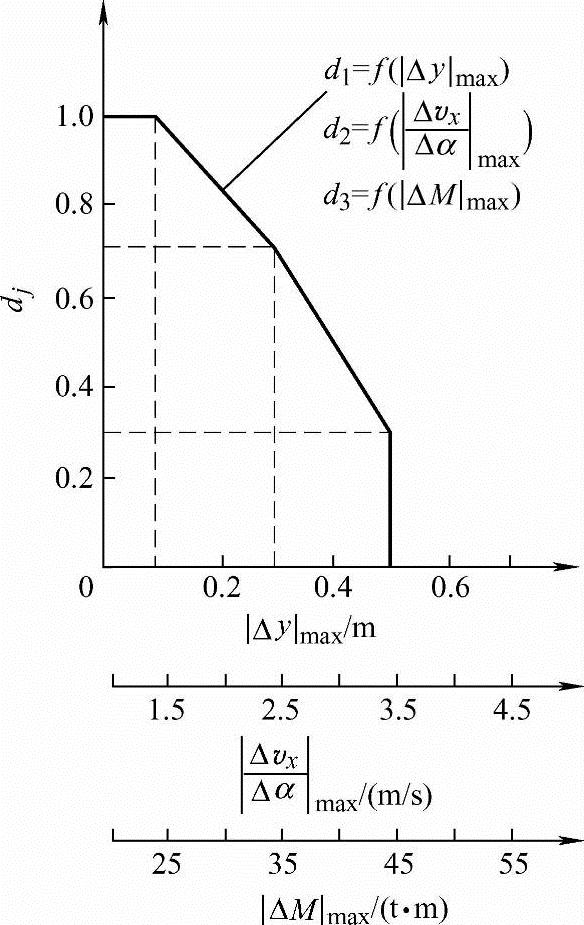
图6-10 门座式起重机变幅四杆机构优化设计的功效系数

（4）在变幅四杆机构的设计中，倾覆力矩值是一项很重要的设计指标，而其大小是臂架摆角α的函数，即M=M（α）。从理论上说，整个变幅过程中M=0为其最理想的情形（自平衡机构），但这是不易实现的。因此，在设计时希望做到：

1）在变幅距离较小时，希望作用有能恢复机构正常位置趋势的负力矩，如图6-11a所示，即M₁=M（α）有一定的负值。

2）在变幅距离较大时，希望作用有恢复正常位置趋势的正力矩，如图6-11b所示即M₂=M（α）有一定的正值。

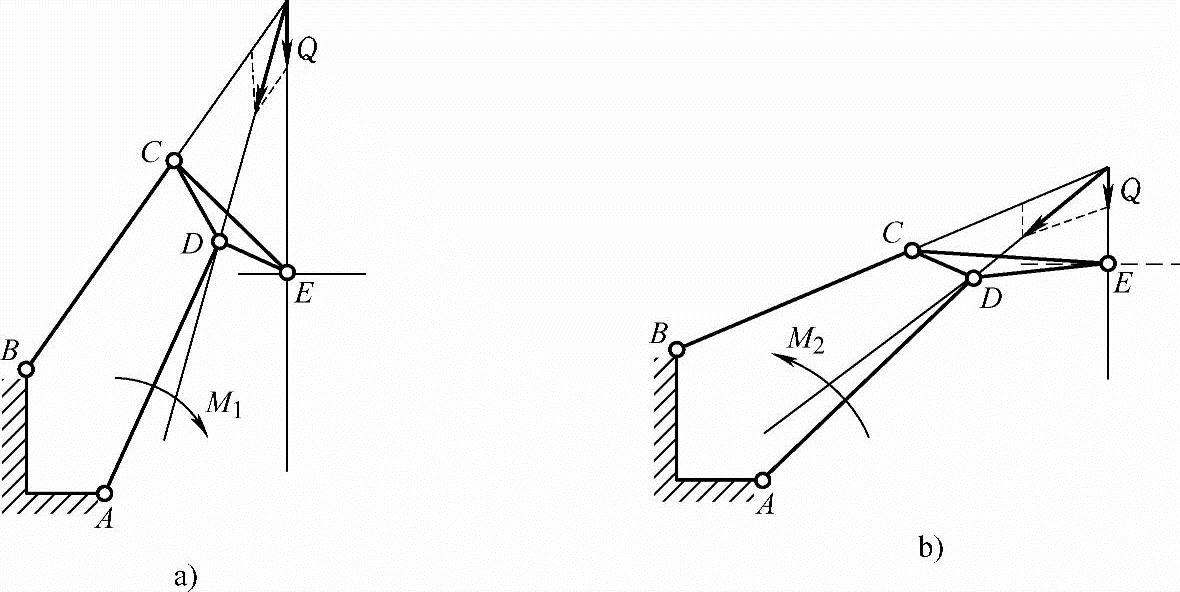
图6-11 门座式起重机变幅四杆机构极限位置时所要求的倾覆力矩

a）最小变幅 b）最大变幅

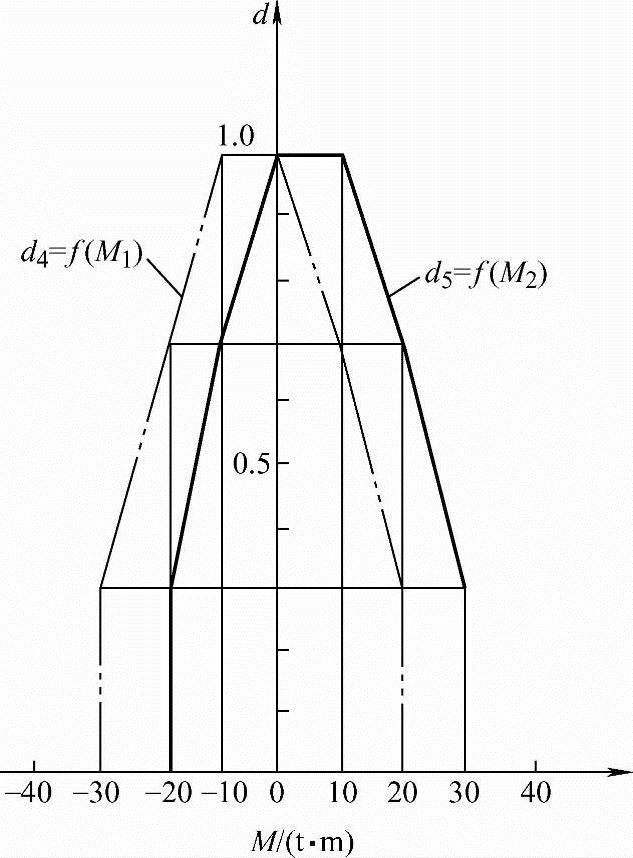
图6-12 倾覆力矩的功效系数

根据这两项设计指标的要求，可按图6-12所示的功效系数函数来定义。例如，对于力矩M₁，最理想的情况是当-10t·m≤M₁＜0t·m时，其功效系数值取d₄=1。当然也应该允许出现较大的负力矩或一个不很大的正力矩，但当M₁＜-30t·m和20t·m＜M₁时都定义为不可接受的方案，即取d₄=0。对于力矩M₂也按类似的方法来定义功效系数d₅。这样，就可得d₄=f（M₁）和d₅=f（M₂）的功效系数函数。

综上所述，起重机四杆变幅机构优化设计的模型为

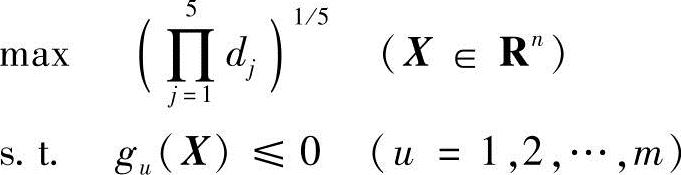
对于起重量10t、工作高度为14.5m，最小变幅距离6m、最大变幅距离27m的港口起重机其计算结果列于表6-1。

表6-1 港口起重机优化设计的各项技术指标

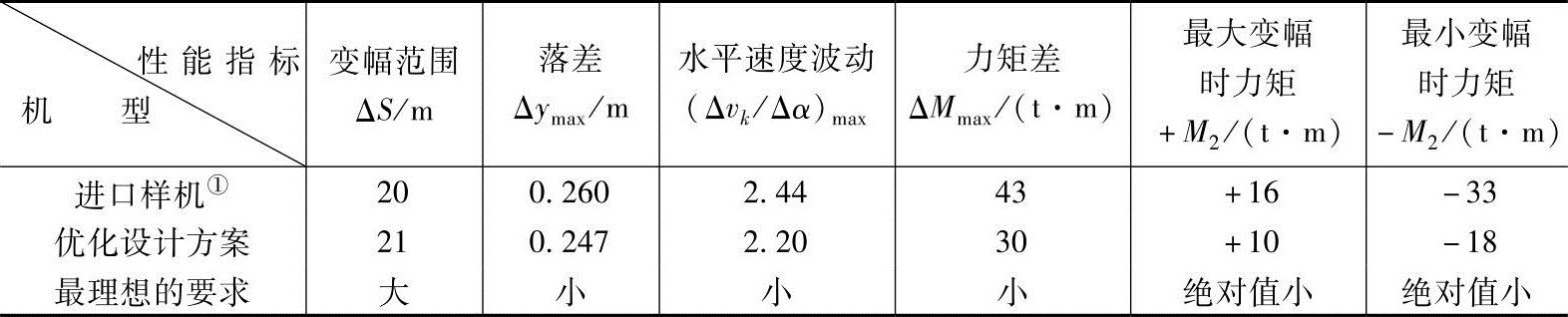
①是近年从国外引迸的同类机型中性能最好的一种产品（DB-10型）。

从表中所列的各项性能指标值可以看出，优化设计结果不仅明显地改善了产品的技术指标的设计水平，而巨也赶上并超过了国外某些同类产品的性能指标。