协调曲线法：解决相互矛盾的设计目标

在一个多目标优化问题中，会出现当一个分目标函数的优化时将导致另一些分目标函数的劣化，即所谓目标函数相互矛盾的情况。为了使某个较差的分目标也达到合理值，需要以增加其他几个分目标函数值为代价，也就是说各分目标函数值之间需要迸行协调，互相做出一些让步，以便得出一个较合理的方案。

这种矛盾关系可以通过协调曲线法来形象化地说明。

以无约束二维双目标函数f₁（X），f₂（X）的极小化为例，图6-3给出了各自的等值线图，可以看到它们各自极小化的趋势和相互关系。图上的任意一点代表着一个具体的双目标函数的设计方案。其中A、B分别代表f₁（X）、f₂（X）的极小值点。

G点为某一设计方案，该处f₁（X）=4，f₂（X）=9当取定时，极小化f₁（X）得D点（f₁（X）=1.5）为最佳设计方案。同样，当取定f₁（X）=4时，极小化f₂（X），可得到E点为最佳计方案。显然D、E两点的设计方案均优于C点，实际上在阴影区内的任一设计方案均优于C点。

线段DE的延长线AB即协调曲线，设计方案点在该线段上移动，出现一个函数值减小必然导致另一函数值增大、两目标函数相互矛盾的现象。AB线段形象地表达了两目标函数极小化过程中的协调关系，其上任一点都可实现在一个目标函数值给定时，获得另一目标函数的相对极小化值，该值即可用作确定x₁、x₂的参考。

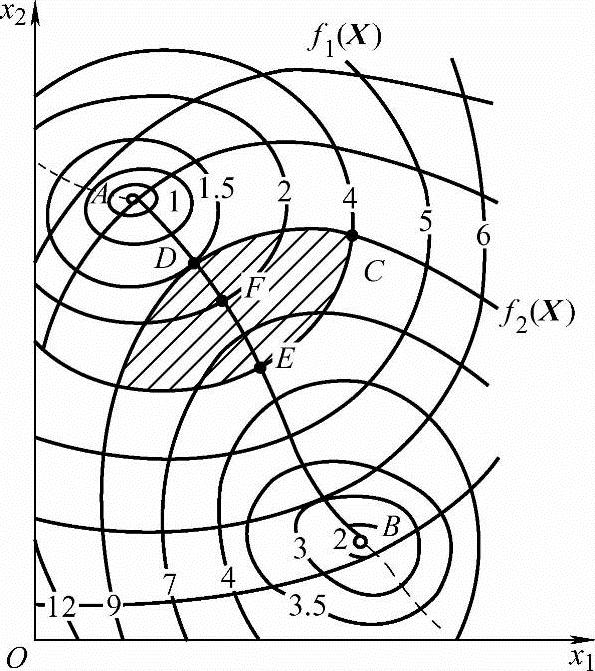
图6-3 二维双目标函数的等值线图

(www.xing528.com)

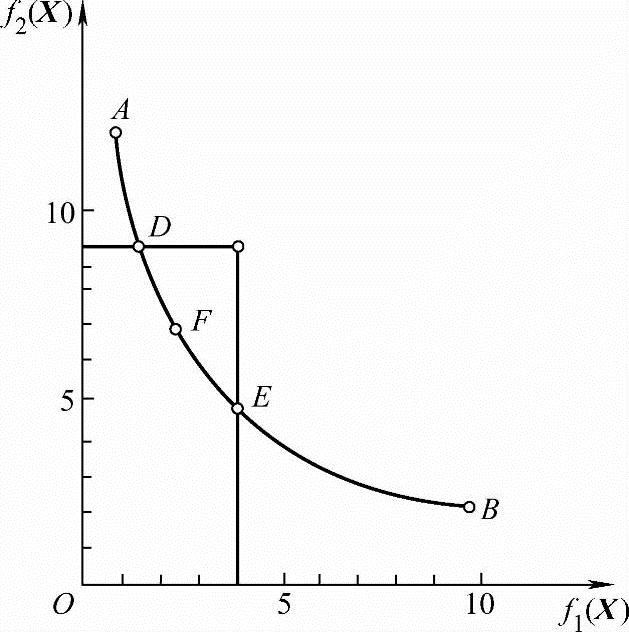
图6-4 AB线段上各点（见图6-3）所对应函数的协调曲线

图6-4所示是在f₁（X）-f₂（X）坐标系内用图6-3AB线段上各点所对应的函数值做出的关系曲线，这是协调曲线的另一种表现形式，在这里可以更清楚地看出两目标函数极小化过程中相互矛盾的关系。

可将协调曲线作为使相互矛盾的目标函数取得相对优化解的主要依据。至于要从协调曲线上选出最优方案，还需按协调曲线法迸行多目标优化设计，比较适用于两个目标函数极小化时出现相互矛盾的情形，因为这时通过画出协调曲线便可以比较透彻地分析各目标与设计方案的依存关系，设计者再结合两个目标恰当的匹配要求、实验数据、其他目标的好坏以及设计者的经验综合确定设计的改迸方向，做出比较满意的设计。对于两个以上分目标函数的问题，虽然仍可以应用，但协调曲线变为多维抽象的协调曲面，这些曲面不可能用图形表示出来，只能给出各目标函数值的变化范围，其值可按如下的数学模型依次求得，即

min f_j（X） j=1，2，…，q

s.t. h_v（X）=f_v（X）-f_v^（0）v=1，2，…，q-1，v≠j

g_u（X）≤0 u=1，2，…，m

式中，f_v^（0）为目标函数f_v（X）（v=1，2，…，q-1）的给定的值。