主要目标法：兼顾多目标最优化

主要目标法的基本思想是根据总体技术条件，在求最优解的各分目标函数f₁（X）、f₂（X）、…、f_L（X）中选定其中一个作为主要目标函数，而将其余L-1个分目标函数分别给一限制值后，使其转化为新的约束条件。这样抓住主要目标，同时兼顾其他目标，从而构成一个新的单目标最优化问题迸行求优。

例如，一个具有两个分目标函数f₁（X），f₂（X）构成的多目标优化问题，其式为

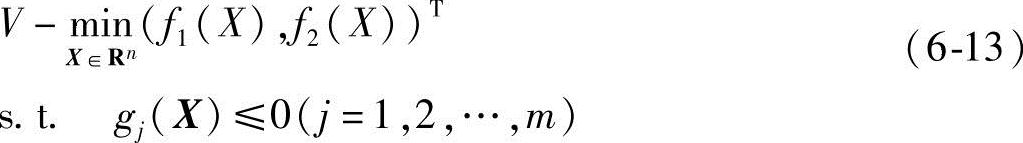
假定经分析后f₁（X）取作主要目标函数，f₂（X）则为次要目标函数，把次要目标函数加上一个约束f₂^（0），使

f₂（X）≤f₂^（0） （6-14）

f₂^（0）为一事先给定的限制值（显然它不能小于f₂（X）的最小值）。这样就把式（6-13）表示的原多目标最优化问题转化为求以下的单目标最优化问题：

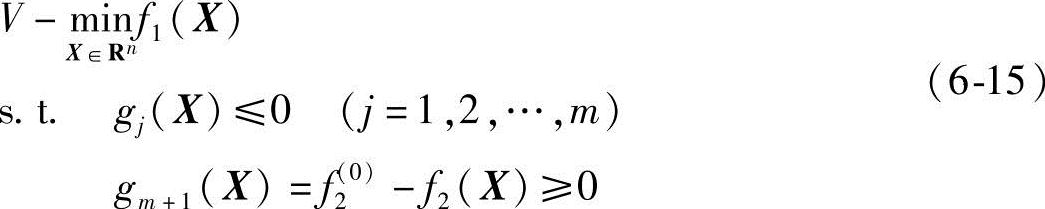
图6-2表明g_j（X）≥0（j=1，2，3，4）构成的多目标优化问题的可行域。(www.xing528.com)

X₁^*、X₂^*分别为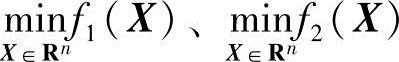的最优点。

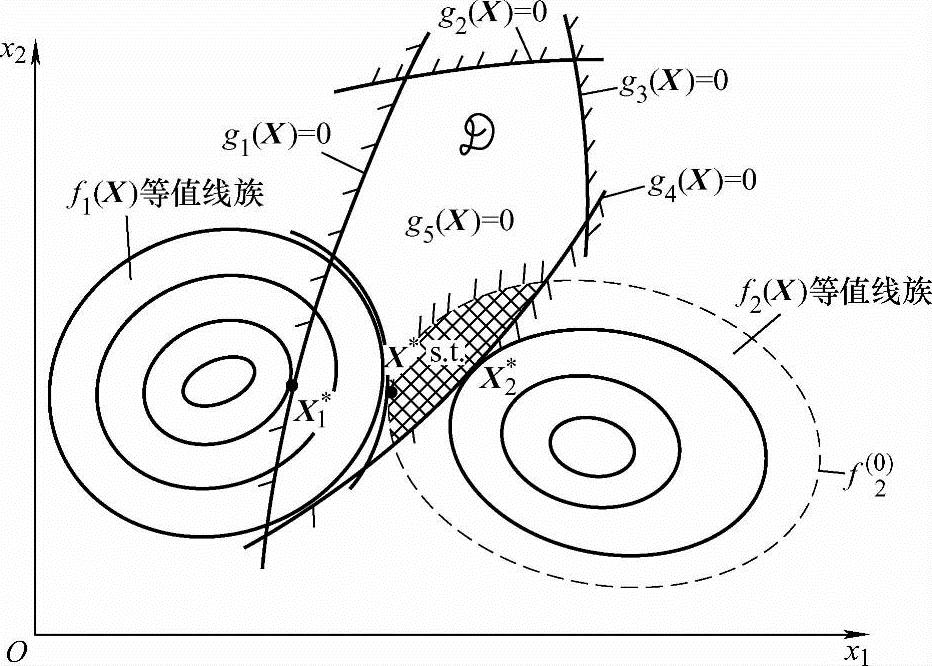
图6-2 两个目标函数的可行域图

现将f₂（X）转化成g₅（X）=f₂^（0）-f₂（X）≥0的新的约束条件，这样原多目标优化问题转变为f₁（X）在由g_j（X）≥0（j=1，2，3，4，5）构成的新的可行域s.t.内（阴影内）的单目标优化问题。显然X*是原多目标优化问题的最优点。

由此，也可把任意的多目标优化问题转化成单目标优化问题。其方法归纳如下：

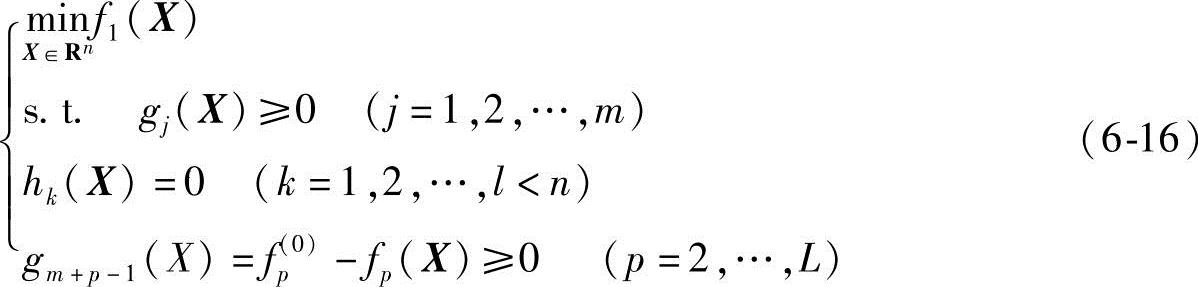
式中，f₁（X）为主要目标函数。