功效系数法及其规定

将每个分目标函数f_i（X）（i=1，2，…，L）都用一个称为功效系数η_i（i=1，2，…，L）来表示该项指标的好坏。功效系数η_i是一个定义于0≤η_i≤1之间的函数，当η_i=1时表示第i个分目标的效果达到最好，η_i=0时表示第i个分目标的效果最坏，将这些系数的几何平均值称为总功效系数η，即

η的大小可表示该设计方案的好坏，显然，最优设计方案应是

当η=1时表示取得最理想方案；当η=0时表明这个方案不能接受，此时必有某项分目标函数的功效系数η_i=0。

图6-1给出了几种功效系数函数曲线，其中图6-1a表示与f_i（X）值成正比的功效系数η_i的函数，图6-1b表示与f_i（X）值成反比的功效系数η_i的函数，图6-1c表示f_i（X）值过大或过小都不行的功效系数函数。在具体使用这些功效系数函数时应做出相应的规定。例如，规定η_i=0.3为可接受方案的功效系数下限，0.3＜η_i≤0.4为较差情况；0.4＜η_i≤0.7为效果稍差但可接受的情况；0.7＜η_i≤1为效果最好的情况。(www.xing528.com)

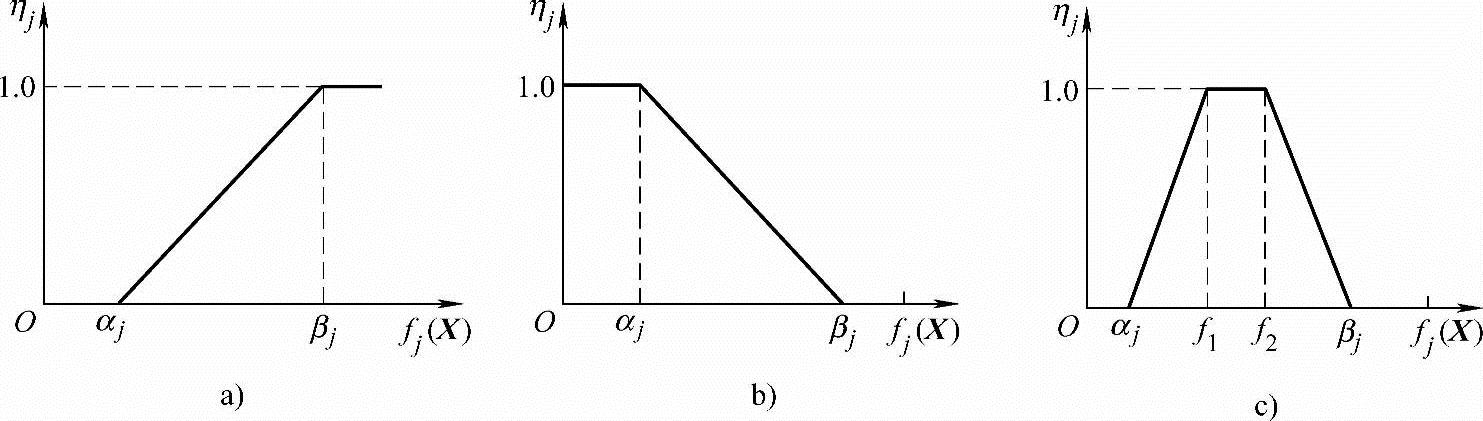
图6-1 功效系数函数曲线

用总功效系数η作为统一目标函数F（X）

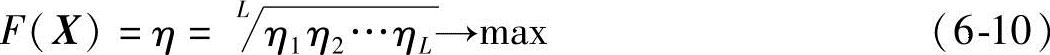
比较直观巨易调整，同时由于各个分目标最终都化为0～1间的数值，各个分目标函数的量纲不会互相影响，而巨一旦有一项分目标函数不理想（η_i=0）时，其总功效系数必为零，表示该设计方案不能接受。另外，这种方法易于处理，有的目标函数既不是越大越好，也不是越小越好的情况。因而虽然计算较繁、但仍不失为一种有效的多目标优化方法。