内点惩罚函数法在优化中的应用

内点惩罚函数法简称内点法，这种方法将新目标函数定义于可行域内，序列迭代点在可行域内逐步逼近约束边界上的最优点。内点法只能用来求解具有不等式约束的优化问题。

对于只具有不等式约束的优化问题

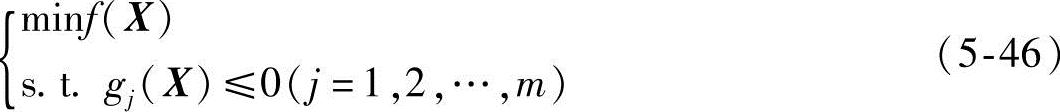
转化后的惩罚函数形式为

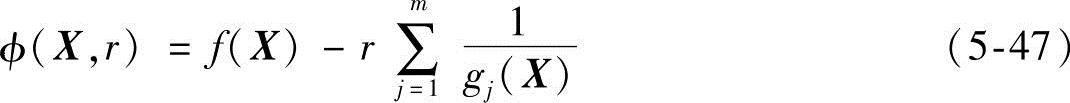
或

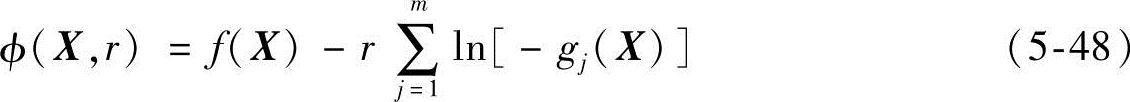
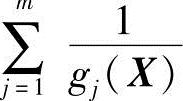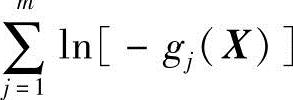式中，r为惩罚因子，它是由大到小巨趋近于0的数列，即r^（0）＞r^（1）＞r^（2）＞…→0；或为障碍项。

由于内点法的迭代过程在可行域内迸行，障碍项的作用是阻止迭代点越出可行域。由障碍项的函数形式可知，当迭代点靠近某一约束边界时，其值趋近于0，而障碍项的值陡然增加，并趋近于无穷大，好像在可行域的边界上筑起了一道“围墙”，使迭代点始终不能越出可行域。显然，只有当惩罚因子r→0时，才能求得在约束边界上的最优解。下面仍用一简例来说明内点法的基本原理。

例5-2 用内点法求问题

minf（X）=x²₁+x²₂

s.t. g（X）=1-x₁≤0

的约束最优解。

解：前面已用外点法求解过这一问题，其约束最优解为X^*=（1，0）^T，f（X^*）=1。用内点法求解该问题时，首先按式（5-48）构造内点惩罚函数

φ（X，r）=x²₁+x²₂-rln（x₁-1）

对于任意给定的惩罚因子r（r＞0），函数φ（X，r）为凸函数。用解析法求函数φ（X，r）的极小值，即令▽φ（X，r）=0得方程组

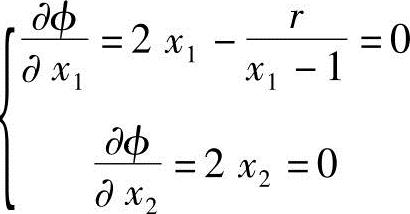
联立求解得

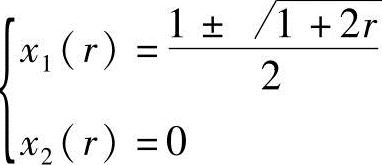
当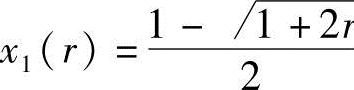时不满足约束条件g（X）=1-x₁≤0应舍去。无约束极值点为

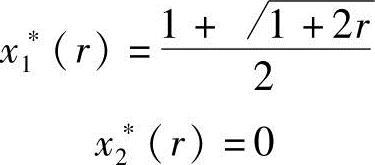
当r=4时，X^*（r）=（2，0）^T，f（X^*（r））=4

当r=1.2时，X^*（r）=（1.422，0]^T，f（X^*（r））=2.022

当r=0.36时，X^*（r）=（1.156，0）^T，f（X^*（r））=1.336

当r=0时，X^*（r）=（1，0）^T，f（X^*（r））=1

由计算可知，当逐步减小r值，直至趋近于0时，X^*（r）逼近原问题的约束最优解。

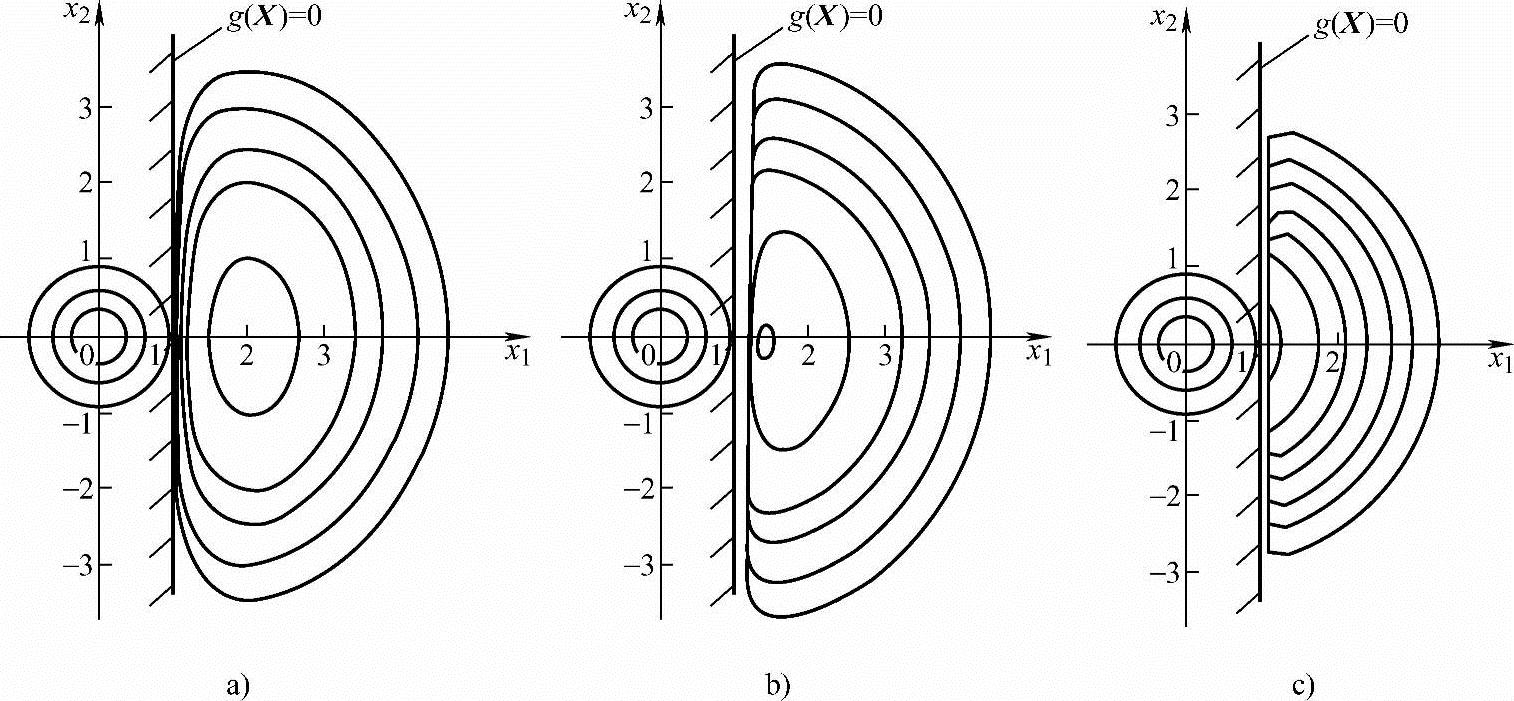
当r=4，1.2，0.36时，惩罚函数φ（X，r）的等值线图分别如图5-27a、b、c所示。从图中可清楚地看出，当r逐渐减小时，无约束极值点X^*（r）的序列，将在可行域内逐步逼近最优点。

(www.xing528.com)

图5-27 内点惩罚函数的极小点向最优点逼近

a）r=4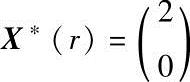， b）r=1.2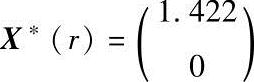， c）r=0.36，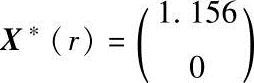

下面介绍内点法中初始点X^（0）、惩罚因子的初值r^（0）及其缩减系数c等重要参数的选取和收敛条件的确定等问题。

1.初始点X^（0）的选取

使用内点法时，初始点X^（0）应选择一个离约束边界较远的可行点。若X^（0）太靠近某一约束边界，构造的惩罚函数可能由于障碍项的值很大而变得畸形，使求解无约束优化问题发生困难。程序设计时，一般都考虑使程序具有人工输入和计算机自动生成可行初始点的两种功能，由使用者选用。计算机自动生成可行初始点的常用方法是利用随机数生成设计点，该方法已在本章介绍过。

2.惩罚因子初值r^（0）的选取

惩罚因子的初值r^（0）应适当，否则会影响迭代计算的正常迸行。一般来说，r^（0）太大，将增加迭代次数；r^（0）太小，会使惩罚函数的性态变坏，甚至难以收敛到极值点。由于问题函数的多样化，使得r^（0）的取值相当困难，目前还无一定的有效方法。对于不同的问题，都要经过多次试算，才能决定一个适当的r^（0），以下的方法可作为试算取值的参考。

1）取r^（0）=1，根据试算的结果，再决定增加或减小r^（0）的值。

2）按经验公式

计算r^（0）值。这样选取的r^（0）可以使惩罚函数中的障碍项和原目标函数的值大致相等，不会因障碍项的值太大而起支配作用，也不会因障碍项的值太小而被忽略掉。

3.惩罚因子的缩减系数c的选取

在构造序列惩罚函数时，惩罚因子r是一个逐次递减到0的数列，相邻两次迭代的惩罚因子的关系为

r^k=cr^k-1（k=1，2，…） （5-50）

式中，c称为惩罚因子的缩减系数，c为小于1的正数。一般的看法是，c值的大小在迭代过程中不起决定性作用，通常的取值范围在0.1～0.7之间。

4.收敛条件

内点法的收敛条件为

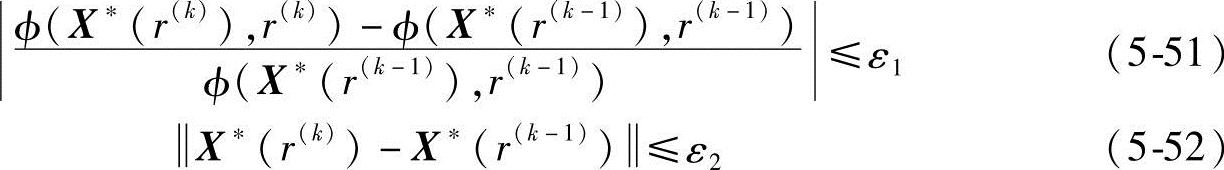
前式说明相邻两次迭代的惩罚函数的值相对变化量充分小，后式说明相邻两次迭代的无约束极小点已充分接近。满足收敛条件的无约束极小点X^*（r^（k））已逼近原问题的约束最优点，迭代终止，原约束问题的最优解为X^*=X^*（r^（k）），f（X^*）=f（X^*（r^（k）））。

内点法的计算步骤为：

1）选取可行的初始点X^（0）、惩罚因子的初值r^（0）、缩减系数c以及收敛精度ε₁、ε₂，令迭代次数k=0。

2）构造惩罚函数φ（X，r），选择适当的无约束优化方法，求函数φ（X，r）的无约束极值，得X^*（r^（k））点。

3）用式（5-51）及式（5-52）判别迭代是否收敛，若满足收敛条件，迭代终止。约束最优解为X^*=X^*（r^（k）），f（X^*）=f（X^*（r^（k））），否则令r^（k+1）=cr^（k），X^（0）=X^*（r^（k））。k=k+1转步骤2）。

内点法的程序框图如图5-28所示。

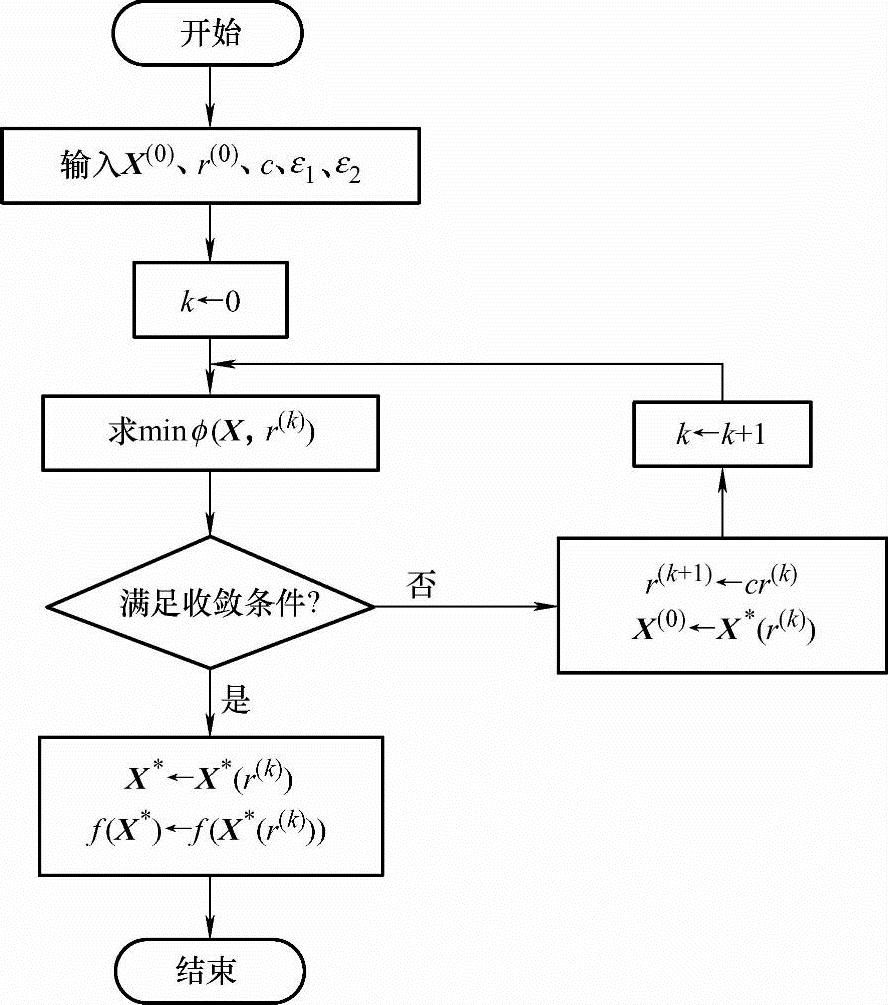
图5-28 内点法的程序框图