使用外点惩罚函数法提高优化算法效率

外点惩罚函数法简称外点法。这种方法和内点法相反，新目标函数定义在可行域之外，序列迭代点从可行域之外逐渐逼近约束边界上的最优点。外点法可以用来求解含不等式和等式约束的优化问题。

对于约束优化问题

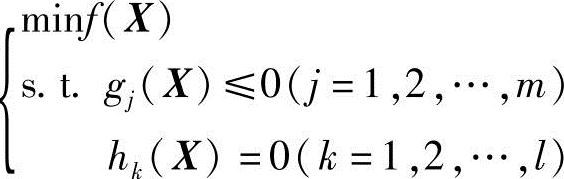
转化后的外点惩罚函数的形式为

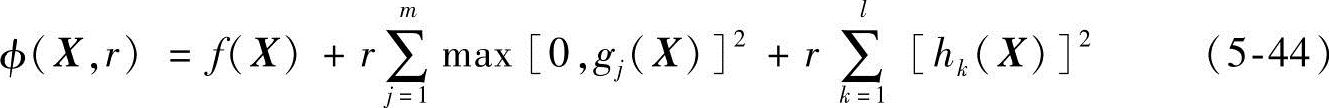
式中，r为惩罚因子，它是由小到大，巨趋近于∞的数列，即r^（0）＜r^（1）＜r^（2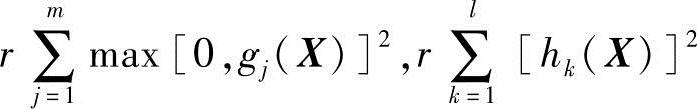）＜…→∞；分别为对应于不等式约束和等式约束函数的惩罚项。

由于外点法的迭代过程在可行域之外迸行，惩罚项的作用是迫使迭代点逼近约束边界或等式约束曲面。由惩罚项的形式可知，当迭代点X不可行时，惩罚项的值大于0。使得惩罚函数φ（X，r）大于原目标函数，这可看成是对迭代点不满足约束条件的一种惩罚。当迭代点离约束边界越远，惩罚项的值越大，这种惩罚越重。但当迭代点不断接近约束边界和等式约束曲面时，惩罚项的值减小，巨趋近于0，惩罚项的作用逐渐消失、迭代点也就趋近于约束边界上的最优点了。

下面用一简例来说明外点法的基本原理。

例5-1 用外点法求问题

minf（X）=x²₁+x²₂

s.t. g（X）=1-x₁≤0

的约束最优解。

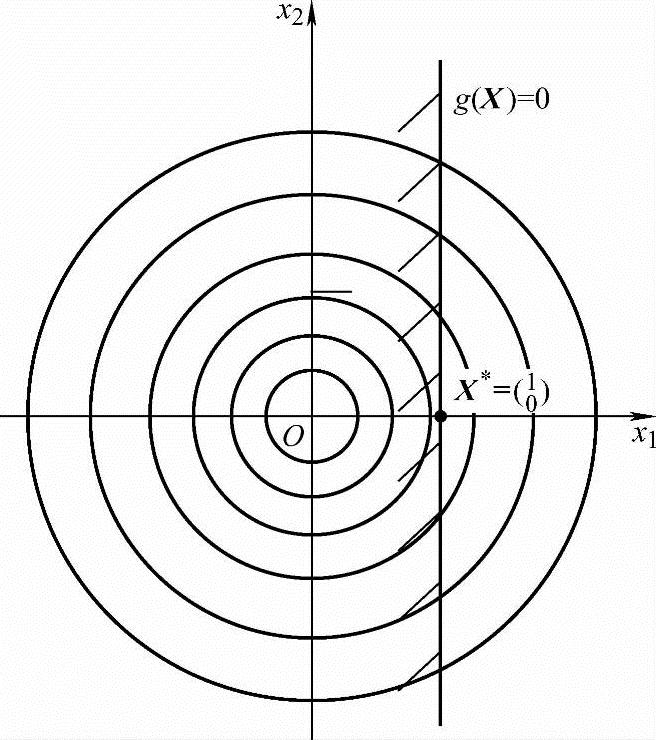
图5-25 例5-1图解

解：如图5-25所示，该问题的约束最优点为X^*=（0，1）^T，它是目标函数等值线，即圆x²₁+x²₂=1和约束函数，即直线1-x₁=0的切点，最优值为f（X^*）=1。用外点法求解时，首先按式（5-44）构造外点惩罚函数

φ（X，r）=x²₁+x²₂+r（1-x₁）²

对于任意给定的惩罚因子r（r＞0），函数φ（X，r）为凸函数，用解析法求φ（X，r）的无约束极小值，即令▽φ（X，r）=0得方程组

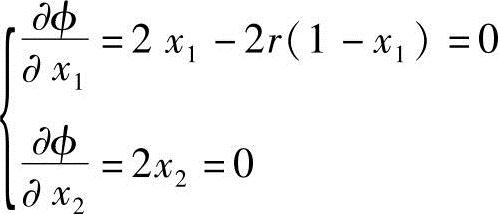
联立求解得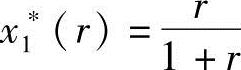(https://www.xing528.com)

x₂^*（r）=0

当r=0.3时，X^*（r）=（0.231，0）^T，f（X^*（r））=0.053

当r=1.5时，X^*（r）=（0.6，0）^T，f（X^*（r））=0.36

当r=7.5时，X^*（r）=（0.882，0）^T，f（X^*（r））=0.778

当r→∞时，X^*（r）=（1，0）^T，f（X^*（r））=1

由计算可知，当逐渐增大r值，直至趋近+∞时，X^*（r）逼近原约束问题的最优解。

当r=0.3，1.5，7.5时，惩罚函数φ（X，r）的等值线图分别示于图5-26a、b、c。

从图中可清楚地看出，当r逐渐增大时，无约束极值点φ（X，r）的序列，将在可行域之外逐步逼近约束最优点。

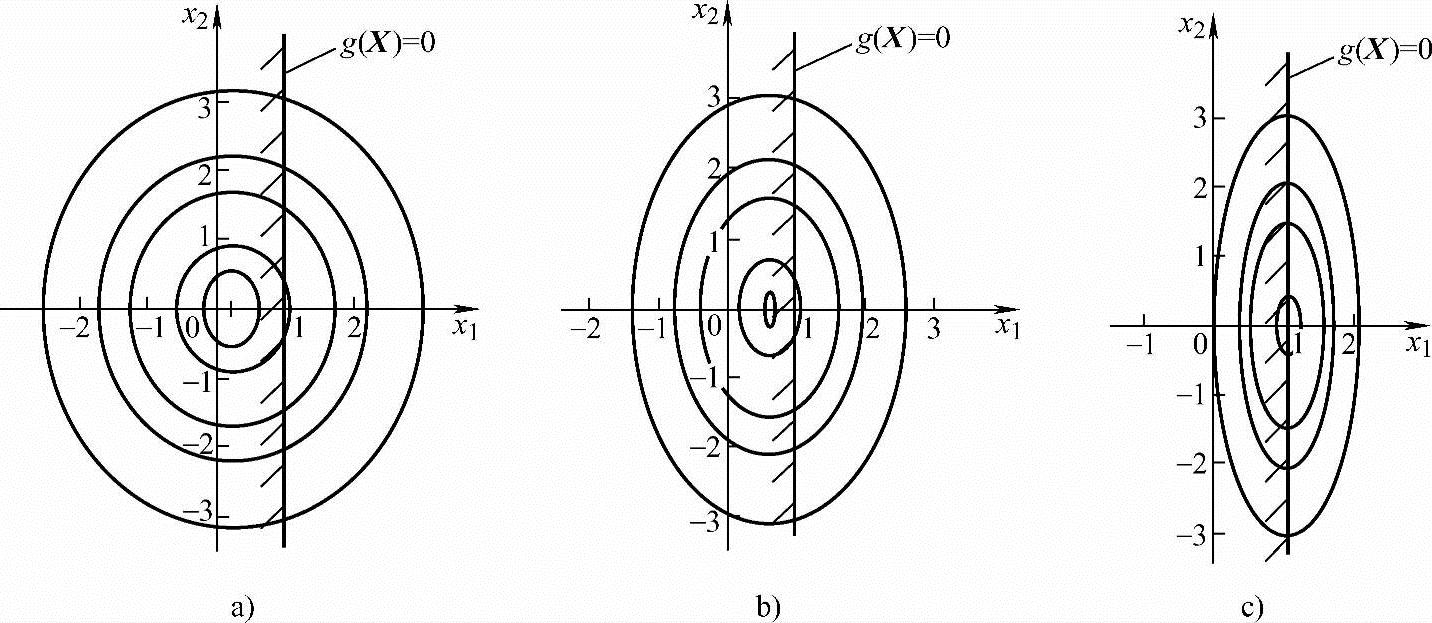
图5-26 外点惩罚函数的极小点向约束最优点逼近

a）r=0.3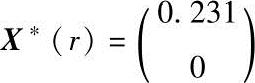， b）r=1.5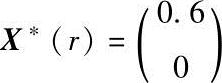， c）r=0.75，X*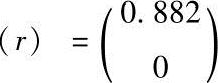

外点法的惩罚因子按下式递增

r^（k）=cr^（k-1）（5-45）

式中，c为递增系数，通常取c=5～10。

与内点法相反，惩罚因子的初值r^（0）若取相当大的值。会使φ（X，r）的等值线变形或偏心，求φ（X，r）的极值将发生困难，但r^（0）取得过小，势必增加迭代次数。所以，在外点法中r^（0）的合理取值也是很重要的。许多计算表明，取r^（0）=1，c=10常常可以取得满意的结果。有时仅用下面的经验公式来计算r^（0）值：

r^（0）=max|r_j^（0）|（j=1，2，…，m）

式中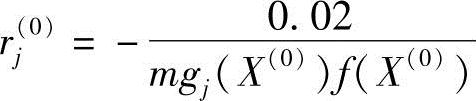，（j=1，2，…，m）

外点法的收敛条件和内点法相同，其计算步骤、程序框图也与内点法相近。