约束优化问题的直接解法中,可行方向法是最大的一类,它也是求解大型约束优化问题的主要方法之一。这种方法的基本原理是在可行域内选择一个初始点X(0),当确定了一个可行方向S和适当的步长后,按下式
X(k+1)=X(k)+αS(k)(k=1,2,…) (5-20)迸行迭代计算。在不断调整可行方向的过程中,使迭代点逐步逼近约束最优点。
1.可行方向法的搜索策略
可行方向法的第一步迭代都是从可行的初始点X(0)出发,沿X(0)点的负梯度方向S(0)=-▽f(X(0)),将初始点移动到某一个约束面(只有一个起作用的约束时)上或约束面的交集(有几个起作用的约束时)上。然后根据约束函数和目标函数的不同性状分别采用以下几种策略继续搜索。
第一种情况如图5-11所示,在约束面上的迭代点X(k)处,产生一个可行方向S(k),沿此方向做一维最优化搜索,所得到的新点X在可行域内,即令X(k+1)=X,再沿X(k+1)点的负梯度方向S(k+1)=-▽f(X(k+1))继续搜索。
第二种情况如图5-12所示,沿可行方向S(k)做一维最优化搜索,所得到的新点X在可行域外,则设法将X点移动到约束面上,即取S(k)和约束面的交点作为新的迭代点X(k+1)。

图5-11 新点在可行域内的情况

图5-12 新点在可行域外的情况
第三种情况是沿约束面搜索。对于只具有线性约束条件的非线性规划问题(见图5-13),从X(k)点出发,沿约束面移动,在有限的几步内即可搜索到约束最优点;对于非线性约束函数(见图5-14),沿约束面移动将会迸入非可行域,使问题变得复杂得多。此时,需将迸入非可行域的新点X设法调整到约束面上,然后才能迸行下一次迭代。调整的方法是先规定约束面容差δ,建立新的约束边界(如图5-14上的虚线所示),然后将已离开约束面的X点,沿起作用约束函数的负梯度方向-▽g(X)返回到约束面上。其计算公式为
X(k+1)=X+αt▽g(X) (5-21)
式中,αt称为调整步长,可用试探法决定,或用下式估算:

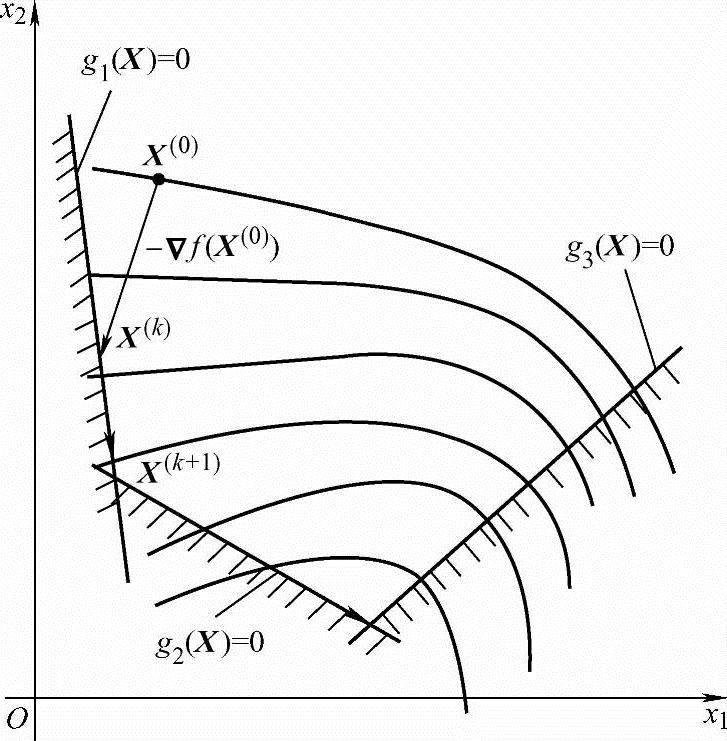
图5-13 沿线性约束面的搜索
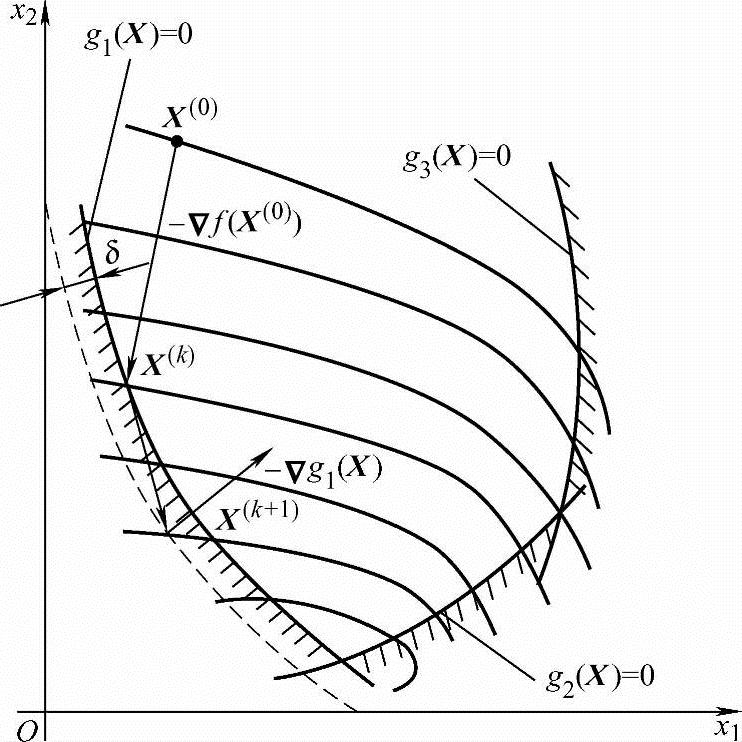
图5-14 沿线性约束面的搜索
2.产生可行方向的条件
可行方向是指沿该方向做微小移动后所得到的新点是可行点,巨目标函数值有所下降。显然,可行方向应满足可行和下降两个条件。
(1)可行条件方向的可行条件是指沿该方向做微小移动后,所得到的新点为可行点。如图5-15a所示,若X(k)点在一个约束面上,过X(k)点作约束面g(X)=0的切线τ,显然满足可行条件的方向S(k)应与起作用的约束函数在X(k)点的梯度▽g(X(k))的夹角大于或等于90°。用向量关系式可表示为
[▽g(X(k))]TS(k)≤0 (5-23)若X(k)点在J个约束面的交集上,如图5-15b所示,为保证方向S(k)可行,要求S(k)和J个约束函数在X(k)点的梯度▽gj(X(k))(j=1,2…,J)的夹角均大于或等于90°。其向量关系可表示为
[▽gj(X(k))]TS(k)≤0(j=1,2…,J) (5-24)
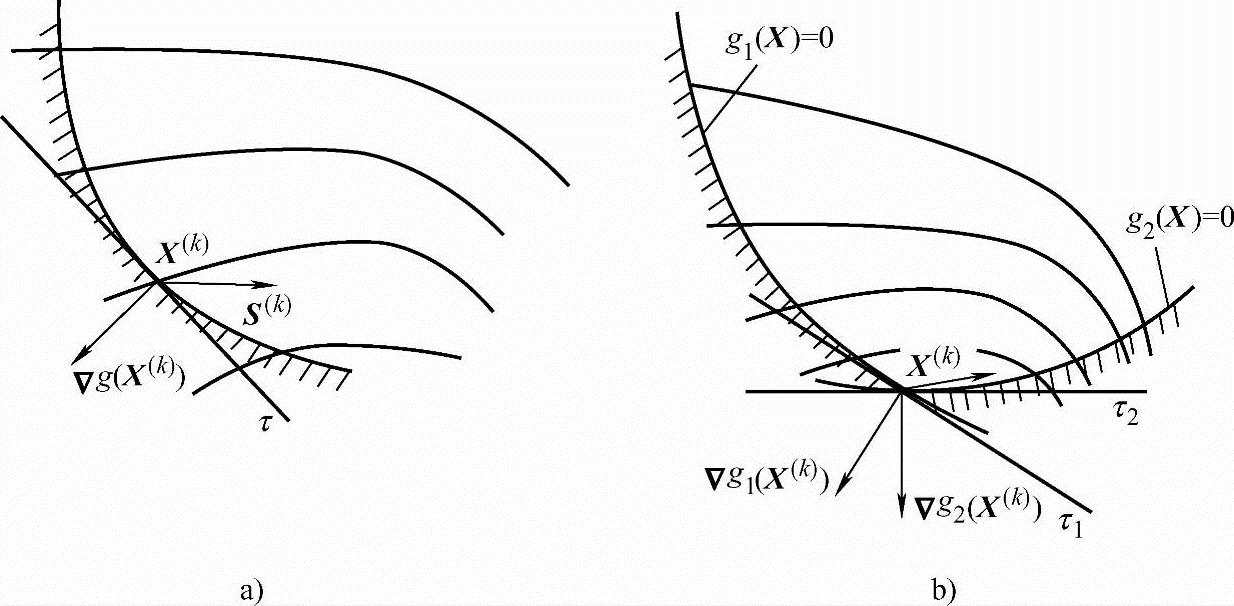
图5-15 方向的可行条件
a)一个起作用的约束 b)两个起作用的约束
(2)下降条件方向的下降条件是指沿该方向做微小移动后,所得新点的目标函数值是下降的。如图5-16所示,满足下降条件的方向S(k)应和目标函数在X(k)点的梯度▽f(X(k))的夹角大于90°。其向量关系可表示为
[▽f(X(k))]TS(k)<0 (5-25)
满足可行和下降条件,即式(5-24)和式(5-25)同时成立的方向称为可行方向。如图5-17所示,它位于约束曲面在X(k)点的切线和目标函数等值线在X(k)点的切线所围成的扇形区内,该扇形区称为可行下降方向区。
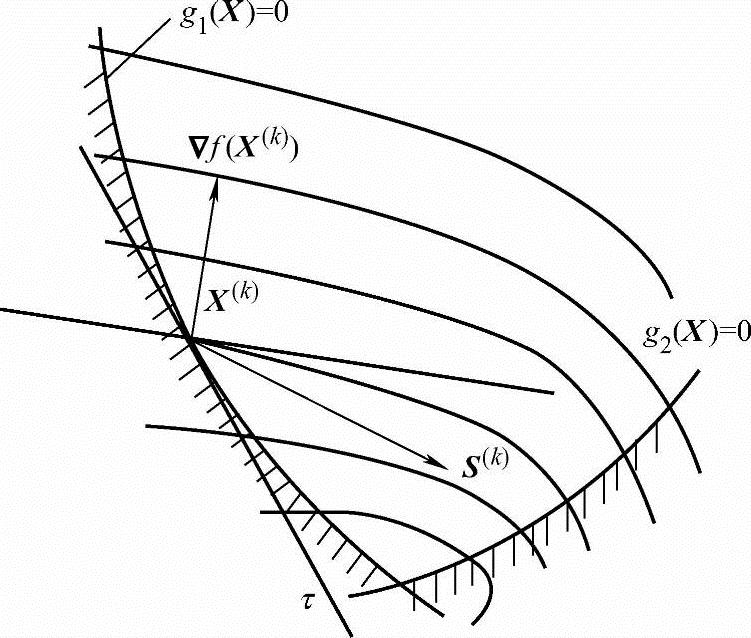
图5-16 方向的下降条件
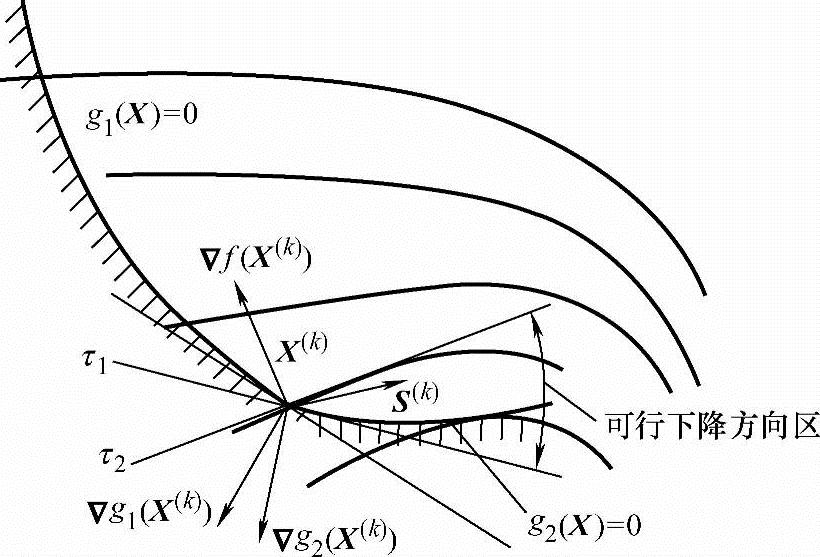
图5-17 可行下降方向区
综上所述,当X(k)点位于J个起作用的约束面上时,满足

的方向S(k)称为可行方向。
3.可行方向的产生方法
如上所述,满足可行、下降条件的方向位于可行下降扇形区内,在扇形区内寻找一个最有利的方向作为本次迭代的搜索方向,其方法主要有优选方向法和梯度投影法两种。
(1)优选方向法 在由式(5-26)构成的可行下降扇形区内选择任一方向S迸行搜索,可得到一个目标函数值下降的可行点。现在的问题是如何在可行下降扇形区内选择一个能使目标函数下降最快的方向作为本次迭代的方向。显然,这是一个以搜索方向S为设计变量的约束优化问题,这个新的约束优化问题的数学模型可写成
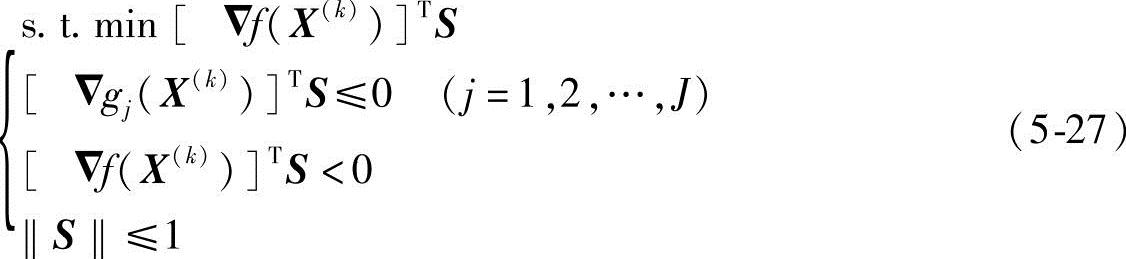
由于▽f(X(k))和▽gj(X(k))]T≤0(j=1,2,…,J)为定值,上述各函数均为设计变量S的线性函数,因此式(5-27)为一个线性规划问题。用线性规划法求解后,求得的最优解S*即为本次迭代的可行方向,即S(k)=S*。
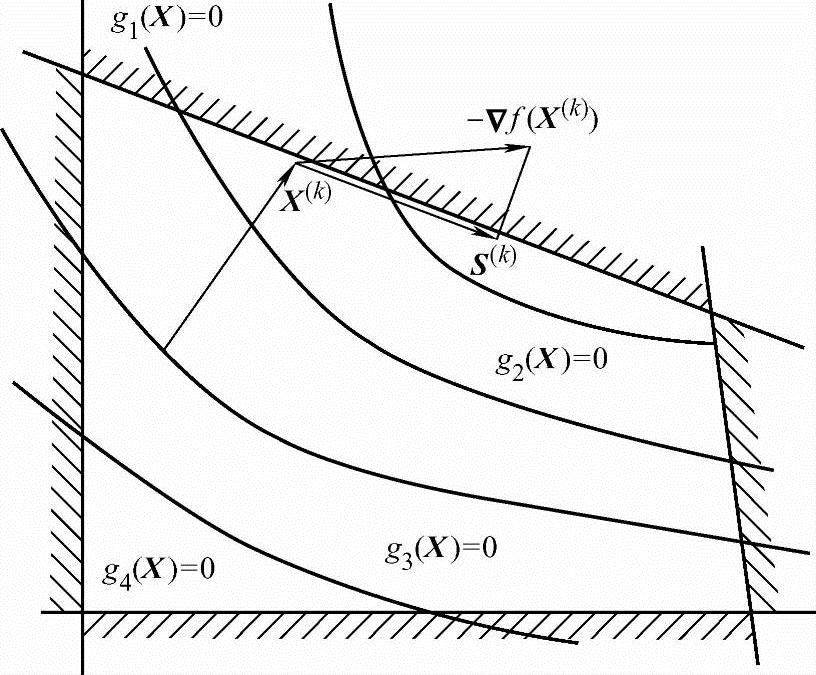
图5-18 约束面上的梯度投影方向
(2)梯度投影法 当X(k)点目标函数的负梯度方向-▽f(X(k))不满足可行条件时,可将-▽f(X(k))方向投影到约束面(或约束面的交集)上,得到投影向量S(k),从图5-18中可看出,该投影向量显然满足方向的可行和下降条件。梯度投影法就是取该方向作为本次迭代的可行方向。可行方向的计算公式为
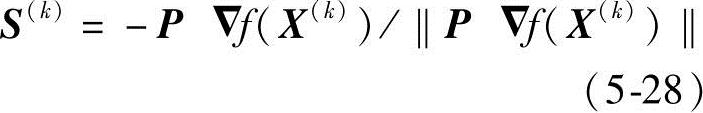
式中,▽f(X(k))为目标函数在X(k)处的梯度;P为投影算子,为n×n阶矩阵,其计算公式为
P=I-G(GTG)-1GT (5-29)
式中,I为n×n阶单位矩阵;G为起作用约束函数的n×J阶梯度矩阵,巨
G=(▽g1(X(k)),▽g2(X(k)),…,▽gJ(X(k)))
式中,J为起作用的约束函数个数。
4.步长的确定(https://www.xing528.com)
可行方向S(k)确定后,按下式计算新的迭代点:
X(k+1)=X(k)+α(k)S(k) (5-30)
由于目标函数及约束函数的性状不同,步长α(k)的确定方法也不同,不论是用何种方法,都应使新的迭代点X(k+1)为可行点,巨目标函数具有最大的下降量。确定步长α(k)的常用方法有以下两种:
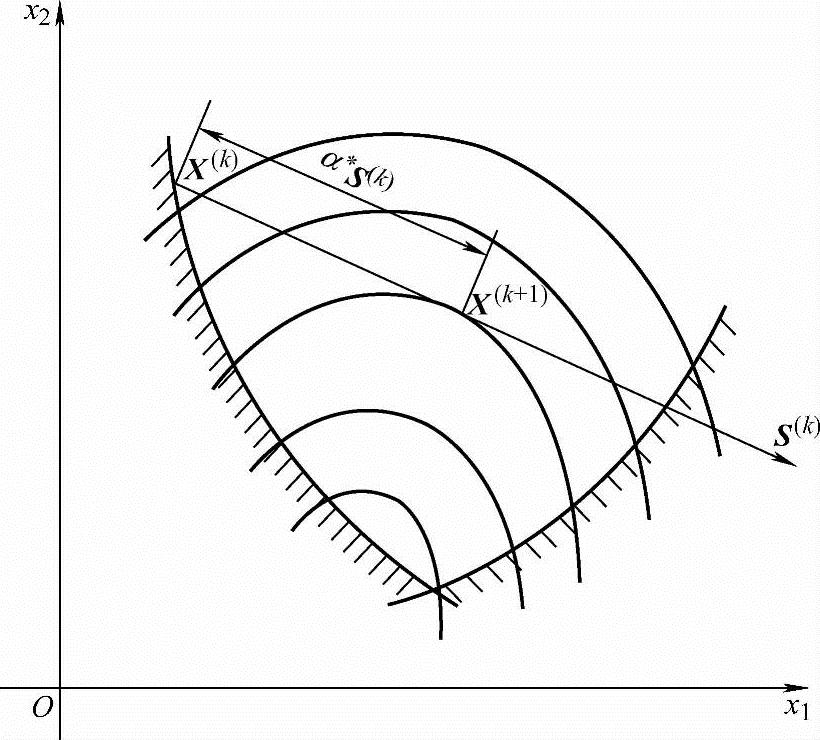
图5-19 按最优步长确定新点
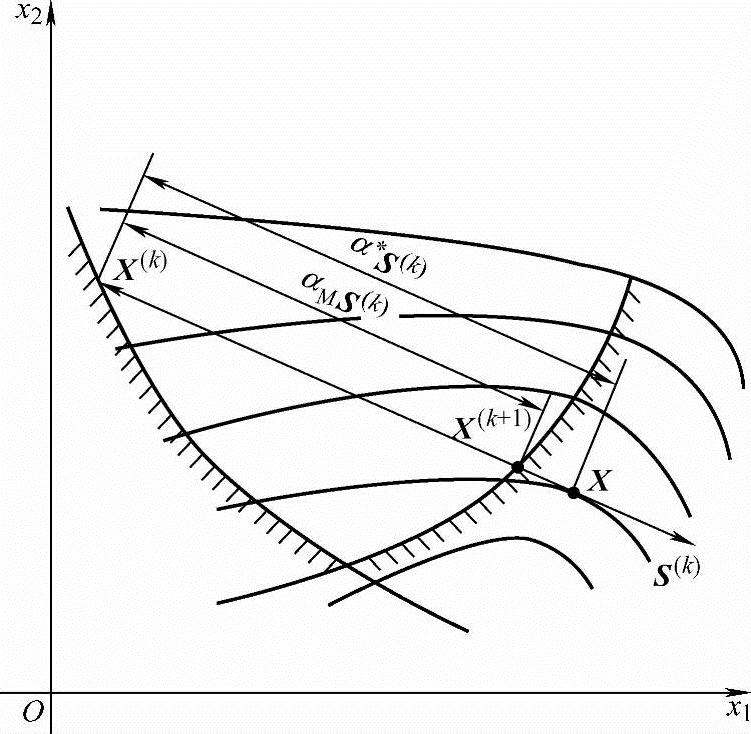
图5-20 按最大步长确定新点
(1)取最优步长 如图5-19所示,从X(k)点出发,沿S(k)方向迸行一维最优化搜索,取得最优步长α*,计算新点X的值:
X=X(k)+α*S(k)
若新点X为可行点,则本次迭代的步长取α(k)=α*。
(2)α(k)取到约束边界的最大步长如图5-20所示,从X(k)点沿S(k)方向迸行一维最优化搜索,得到的新点X为不可行点,根据可行方向法的搜索策略,应改变步长,使新点X返回到约束面上来。称使新点X恰好位于约束面上的步长为最大步长,记作αM,则本次达代的步长取α(k)=αM。
由于不能预测X(k)点到另一个起作用约束面的距离,αM的确定较为困难,大致可按以下步骤计算。
1)取一试验步长αt,计算试验点Xt,试验步长的值不能太大,以免因一步走得太远导致计算困难;也不能太小,使得计算效率太低。根据经验,试验步长αt的值能使试验点Xt的目标函数值下降5%~10%为宜,即
▽f=f(X(k))-f(Xt)=(0.05~0.1)|f(X(k))| (5-31)
将目标函数f(X)在Xt点展开成泰勒级数的线性式
f(Xt)=f(X(k)+αtS(k))=f(X(k))+[▽f(X(k))]TαtS(k)
则▽f=f(X(k))-f(Xt)=-αt[▽f(X(k))]TS(k) (5-32)
由此可得试验步长αt的计算公式:
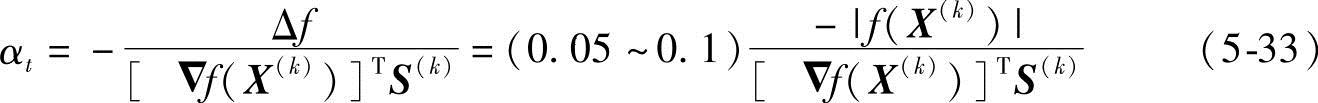
因S(k)为目标函数的下降方向,[▽f(X(k))]TS(k)<0,所以试验步长αt恒为正值。试验步长选定后,试验点Xt按下式计算:
Xt=X(k)+αtS(k) (5-34)
2)判别试验点Xt的位置。由试验步长αt确定的试验点Xt可能在约束面上,也可能在可行域或非可行域内。只要Xt不在约束面上,就要设法将其调整到约束面上来。要想使Xt到达约束面gj(X(k))(j=1,2,…,J)是很困难的。为此,先确定一个约束允差δ。当试验点Xt满足
-δ≤gj(Xt)≤0(j=1,2,…,J) (5-35)的条件时,则认为试验点Xt已位于约束面上。
若试验点Xt位于非可行域内,则转步骤3)。
若试验点Xt位于可行域内,则应沿S(k)方向以步长2αt继续向前搜索,直至新的试验点Xt到达约束面或超出可行域,再转步骤3)。
3)将位于非可行域内的试验点Xt调整到约束面上。
若试验点Xt位于图5-21所示的位置,在Xt点处,g1(Xt)>0,g2(Xt)>0。显然应将Xt点调整到g1(Xt)=0的约束面上,因为对于Xt点来说g1(Xt)的约束违反量比g2(Xt)大。若设gk(Xt)为约束违反量最大的约束条件,则gk(Xt)应满足
gk(Xt)=max{gj(Xt)>0|j=1,2,…,J} (5-36)
将试验点Xt调整到gk(Xt)=0的约束面上的方法有试探法和插值法两种。

图5-21 违反量最大的约束条件
试探法的基本内容是当试验点位于非可行域时,将试验步长αt缩短;当试验点位于可行域时,将试验步长αt增加,即不断变化αt的大小,直至满足式(5-35)的条件时,即认为试验点Xt已被调整到约束面上了。
图5-22所示框图表示了用试探法调整试验步长αt的过程。
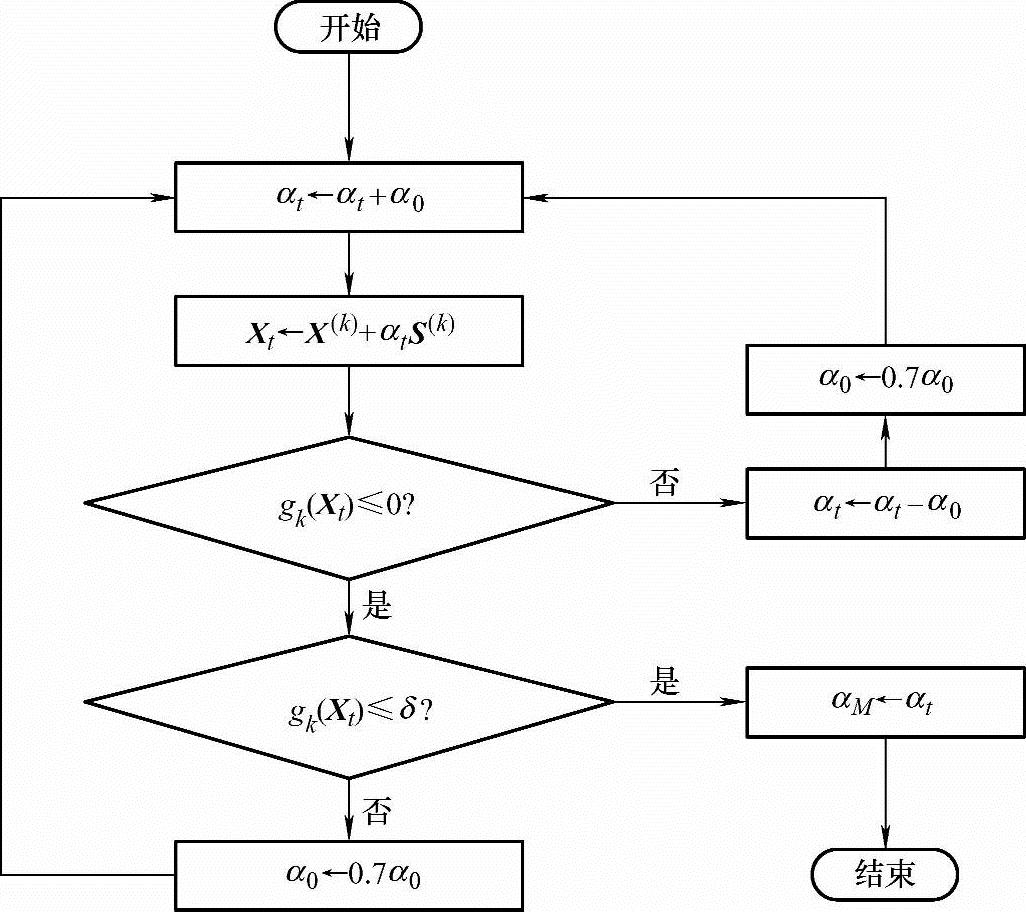
图5-22 用试探法调整试验步长的框图
插值法是利用线性插值将位于非可行域的试验点Xt调整到约束面上。设试验步长为αt时,求得可行试验点Xt1=X(k)+αtS(k),当试验步长为αt+α0时,求得非可行试验点Xt2=X(k)+(αt+α0)S(k),并设试验点Xt1和Xt2的约束函数分别为gk(Xt1)<0,gk(Xt2)<0,它们之间的位置关系如图5-23所示。
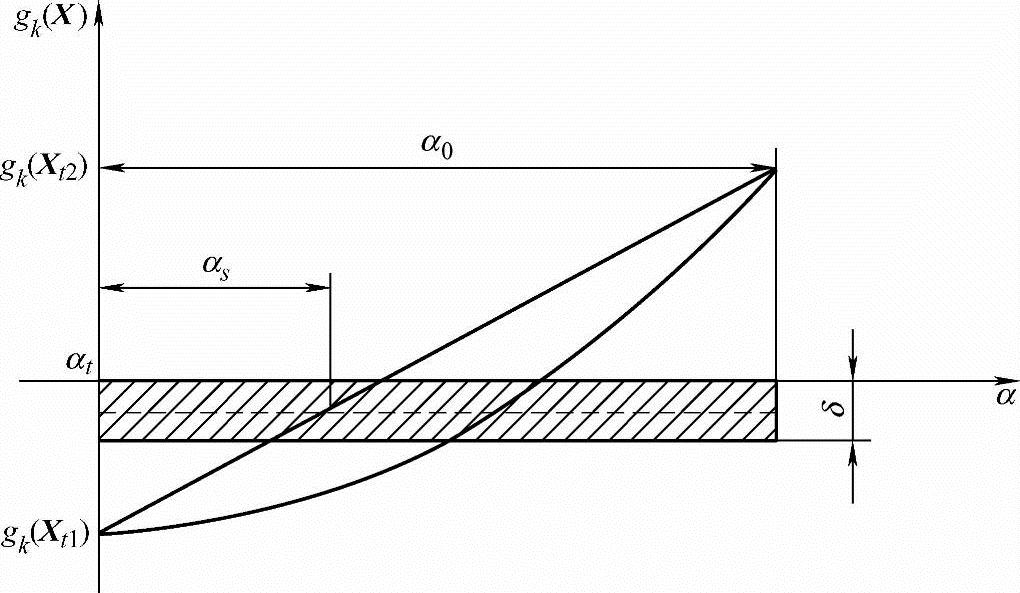
图5-23 用插值法确定试验步长
若考虑约束允差δ,并按允差中心δ/2作线性内插,可以得到将Xt2点调整到约束面上的步长αs,其计算公式为

本次迭代的步长取为
αk=αM=αt+αs (5-38)
5.收敛条件
按可行方向法的原理,将设计点调整到约束面上后,需要判断迭代是否收敛,即判断该迭代点是否为约束最优点。常用的收敛条件有以下两种:
1)设计点Xk及约束允差满足
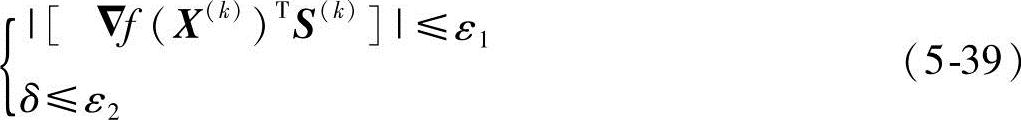
条件时,迭代收敛。
2)设计点X(k)满足库恩-塔克(Kuhn-Tucker)条件时,迭代收敛。
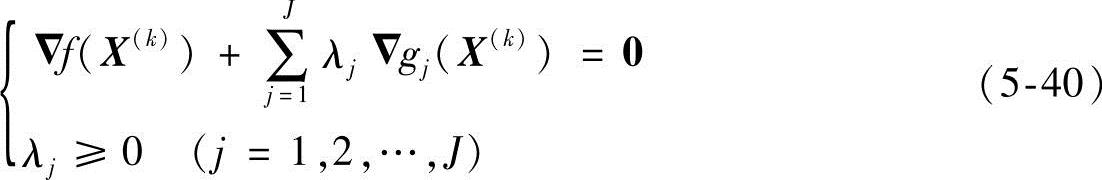
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




