初始复合形的产生及其机制分析

1.初始复合形的形成

复合形法是在可行域内直接搜索最优点，因此，要求初始复合形在可行域内生成，即初始复合形的k个顶点必须都是可行点。

生成初始复合形的方法有以下几种：

1）由设计者决定k个可行点，构成初始复合形。当设计变量较多或约束函数复杂时，由设计者决定k个可行点常常很困难。只有在设计变量少，约束函数简单的情况下，这种方法才被采用。

2）由设计者选定一个可行点，其余的（k-1）个可行点用随机法产生。各顶点按下式计算：

X_j=a+R_j（b-a）（j=1，2，…，k） （5-10）

式中，X_j为复合形中的第j个顶点；a、b分别为设计变量的下限和上限；R_j为在（0，1）区间内的伪随机数。

用式（5-10）计算得到的（k-1）个随机点不一定都在可行域内，因此要设法将非可行点移到可行域内。通常采用的方法是，求出已经在可行域内的L个顶点的中心X_C：

然后将非可行点向中心点移动，即

X_L+1=X_C^+0.5（X_L+1-X_C） （5-12）

若X_L+1仍为不可行点，则利用式（5-12），使其继续向中心点移动。显然，只要中心点可行，X_L+1点一定可以移到可行域内。随机产生的（k-1）个点经过这样的处理后，全部成为可行点，并构成初始复合形。

事实上，只要可行域为凸集，其中心点必为可行点，用上述方法可以成功地在可行域内构成初始复合形。如果可行域为非凸集，如图5-5所示，中心点不一定在可行域之内，则上述方法可能失败。此时可以通过改变设计变量的下限和上限值，重新产生各顶点。经过多次试算，有可能在可行域内生成初始复合形。

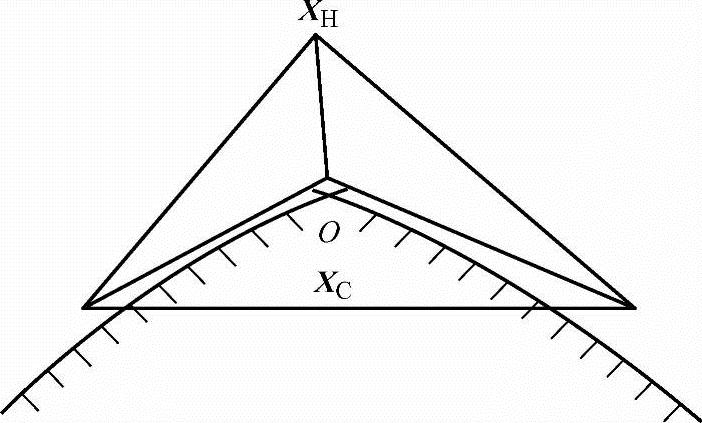
图5-5 中心点X_C为非可行点的情况

3）由计算机自动生成初始复合形的全部顶点。其方法是首先随机产生一个可行点，然后按第二种方法产生其余的（k-1）个可行点。这种方法对设计者来说最为简单，但因初始复合形在可行域内的位置不能控制，可能会给以后的计算带来困难。

2.复合形法的搜索方法

在可行域内生成初始复合形后，将采用不同的搜索方法来改变其形状，使复合形逐步向约束最优点趋近。改变复合形形状的搜索方法主要有以下几种：

（1）反射 反射是改变复合形形状的一种主要策略，其计算步骤为：

1）计算复合形各顶点的目标函数值，并比较其大小，求出最好点X_L、最坏点X_H及次坏点X_G，即

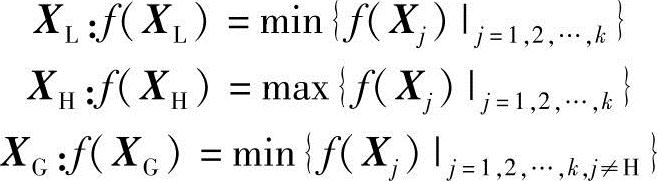
2）计算除去最坏点X_H外的（k-1）个顶点的中心X_C：

3）从统计的观点来看，一般情况下，最坏点X_H和中心点X_C的连线方向为目标函数下降的方向。为此，以X_C点为中心，将最坏点X_H按一定比例迸行反射，有希望找到一个比最坏点X_H的目标函数值为小的新点X_R，X_R称为反射点。其计算公式为

X_R=X_C+α（X_C-X_H） （5-14）

式中，α为反射系数，一般取α=1.3。

反射点X_R与最坏点X_H、中心点X_C的相对位置如图5-6所示。

4）判别反射点X_R的位置，若X_R为可行点，则比较X_R和X_H两点的目标函数值，如果f（X_R）＜f（X_H），则用X_R取代X_H，构成新的复合形，完成一次迭代；如果f（X_R）≥f（X_H），则将α缩小为原来的7/10，用式（5-14）重新计算新的反射点，若仍不可行，继续缩小，直至f（X_R）＜f（X_H）为止。(www.xing528.com)

若X_R为非可行点，则将α缩小为原来的7/10，仍用式（5-14）计算反射点X_R，直至为可行点为止。然后重复以上步骤，即判别f（X_R）和f（X_H）的大小，一旦f（X_R）＜f（X_H），用X_R取代X_H完成一次迭代。

综上所述，反射成功的条件是

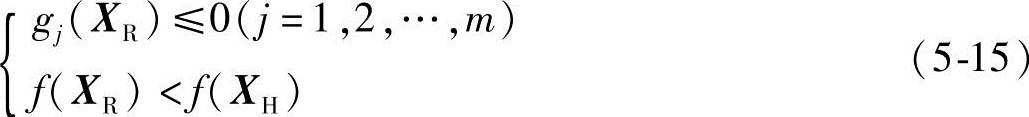
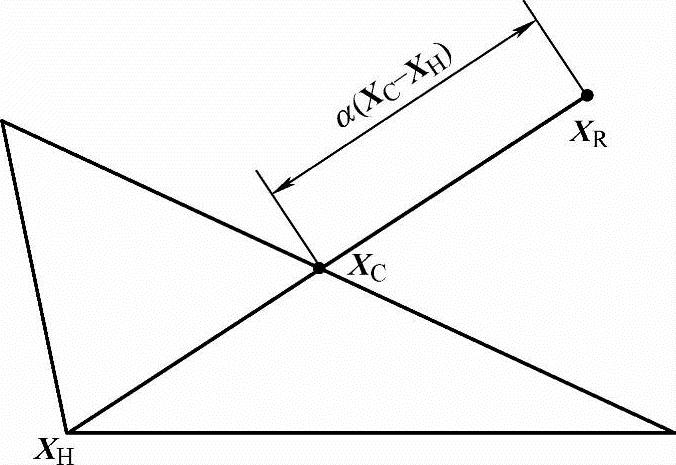
图5-6 X_R、X_H与X_C的相对位置

（2）扩张 当求得的反射点X_R为可行点，且目标函数值下降较多（如f（X_R）＜f（X_C）），则沿反射方向继续移动，即采用扩张的方法，可能找到更好的新点X_E，X_E称为扩张点。其计算公式为

X_E=X_R+γ（X_R-X_C）

式中，γ为扩张系数，一般取γ=1。

扩张点X_E与中心点X_C、反射点X_R的相对位置如图5-7所示。

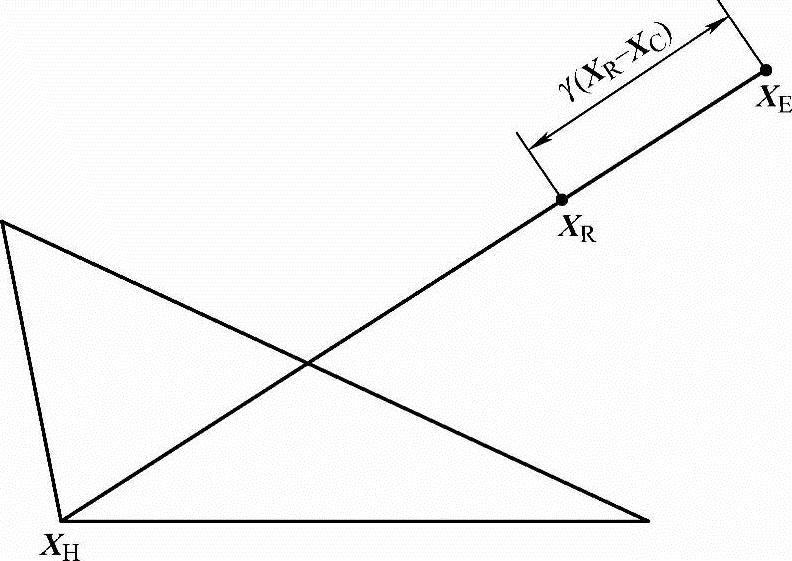
图5-7 X_E与中心点X_C、反射点X_R的相对位置

若扩张点X_E为可行点，且f（X_E）＜f（X_R），则称扩张成功，用X_E取代X_R，构成新的复合形。否则称扩张失败，放弃扩张，仍用原反射点X_R取代X_H，构成新的复合形。

（3）收缩 若在中心点X_C以外找不到好的反射点，还可以在X_C以内，即采用收缩的方法寻找较好的新点X_k，X_k称为收缩点。其计算公式为

X_k=X_H+β（X_C-X_H） （5-16）

式中，β为收缩系数，一般取β=0.7。

收缩点X_k与最坏点X_H及中心点X_C的相对位置如图5-8所示。

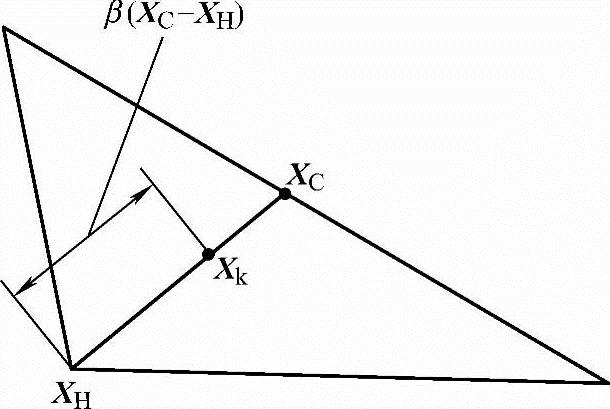
图5-8 X_k与最坏点X_H及中心点X_C的相对位置

若f（X_k）＜f（X_H），则称收缩成功，用X_k取代X_H，构成新的复合形。

（4）压缩 若采用上述各种方法均无效，还可以采取将复合形各顶点向最好点X_L靠拢，即采用压缩的方法来改变复合形的形状。压缩后的各顶点的计算公式为

X_j=X_L-0.5（X_L-X_j）（j=1，2，…，k；j≠L） （5-17）

压缩后的复合形各顶点的相对位置如图5-9所示。

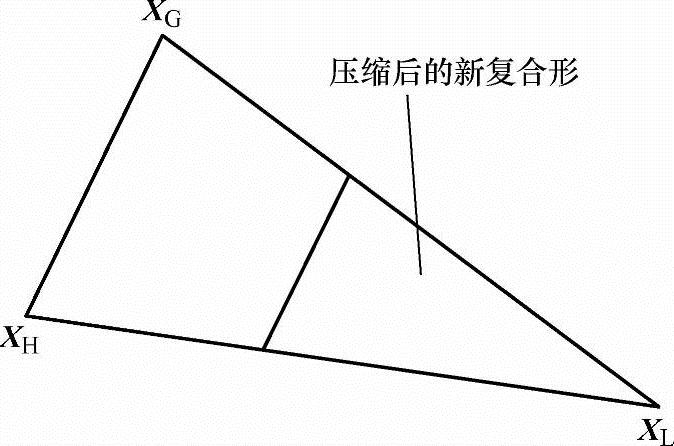
图5-9 复合形的压缩变形

然后，再对压缩后的复合形采用反射、扩张或收缩等方法，继续改变复合形的形状。

除此之外，还可以采用旋转等方法来改变复合形形状。应当指出的是，采用改变复合形形状的方法越多，程序设计越复杂，有可能降低计算效率及可靠性。因此，程序设计时，应针对具体情况，采用某些有效的方法。