无约束优化设计实例示范

例4-1 用最速下降法求目标函数f（X）=x²₁+25x²₂的极小点。

解：取初始点X^（0）=（2，2）^T

则初始点处函数值及梯度分别为

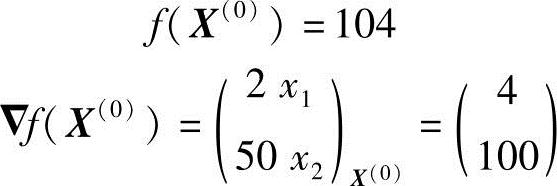
沿负梯度方向迸行一维搜索，有

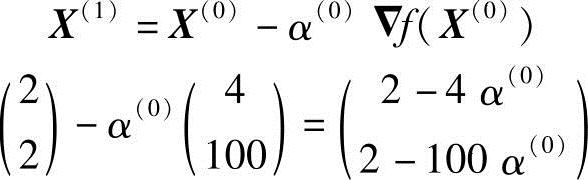
其中，α^（0）为一维搜索最佳步长，应满足极值必要条件，则有

f（X^（1））=minf（X^（0）-α^（0）▽f（X^（0）））=min［（2-4α^（0））2+25（2-100α^（0））2]=minφ（α^（0））

φ′（α^（0））=-8（2-4α^（0））-5000（2-100α^（0））=0

从而算出一维搜索最佳步长

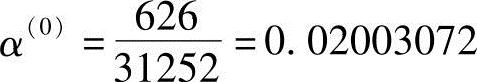
以及第一次迭代设计点位置和函数值

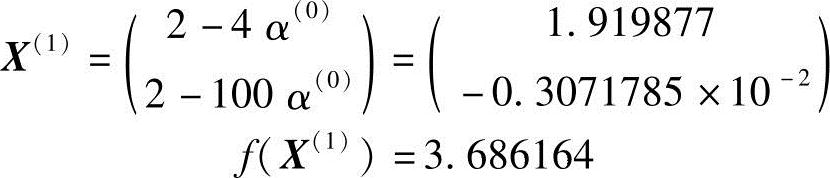
从而完成了最速下降法的第一次迭代。继续做下去，经10次迭代后，得到最优解

X^*=（0，0）^T

f（X^*）=0

例4-2 试用原始牛顿法求目标函数f（X）=60-10x₁-4x₂+x²₁+x²₂-x₁x₂的极小点，初始点X^（0）=（0，0）^T。

解：X^（0）=（0，0）^T，X^（0）处的函数梯度、黑塞矩阵分别为

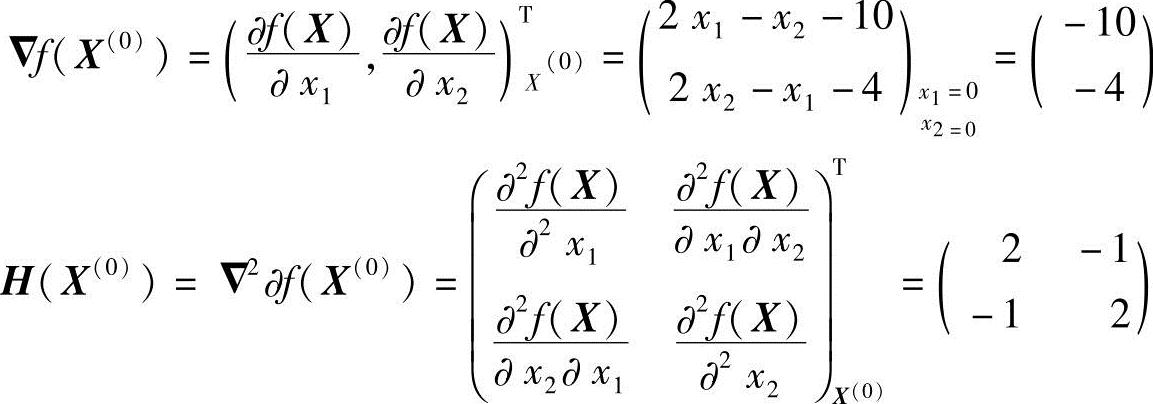
H（X^（0））的伴随矩阵为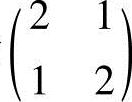，其行列式|H（X^（0））|=3，故H（X^（0））的逆矩阵应为

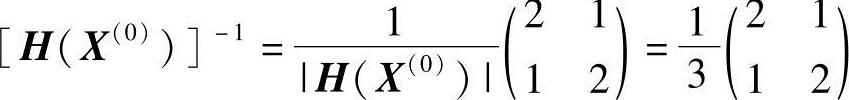
由式（4-7）求下一个迭代点X^（1），得

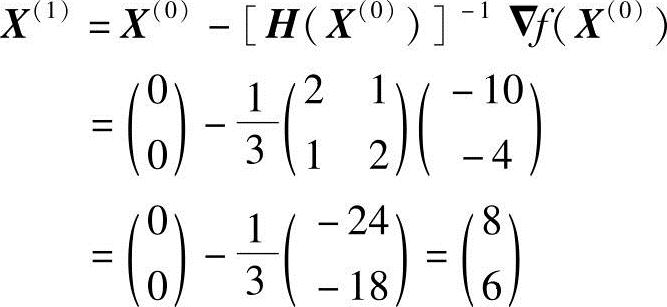
X^（1）=［8，6]^T和目标函数理论极小点X^*=［8，6]^T一致，亦即本例只迭代一次即达目标函数极小点。

由例4-2可以看出，当目标函数f（X）是二次函数时，由于二次泰勒展开函数φ（X）与原目标函数f（X）不是近似而是完全相同的二次式，黑塞矩阵H（X^（k））是一个常数矩阵，由式（4-7）知从任一初始点出发，只需一步迭代即达f（X）的极小点，因此牛顿法也是一种具有二次收敛性的算法。对于非二次函数，若函数的二次性态较强，或迭代点已迸入极小点的邻域，则其收敛速度也是很快的，这是牛顿法的主要优点。但原始牛顿法由于迭代公式中没有步长因子，而是定步长迭代，对于非二次型目标函数，有时会使函数值上升，即出现f（X^（k+1））＞f（X^（k））的情况，这表明原始牛顿法不能保证函数值稳定地下降，在严重的情况下甚至可能造成迭代点列的发散而导致计算失败。

例4-3 目标函数为f（X）=4（x₁+1）2+2（x₂-1）2+x₁+x₂+10，设初始点X^（0）=（0，0）^T，梯度精度ε=0.01，试用阻尼牛顿法求目标函数极小点和极小值。

解：X^（0）=（0，0）^T，X^（0）点处的函数梯度、黑塞矩阵分别为

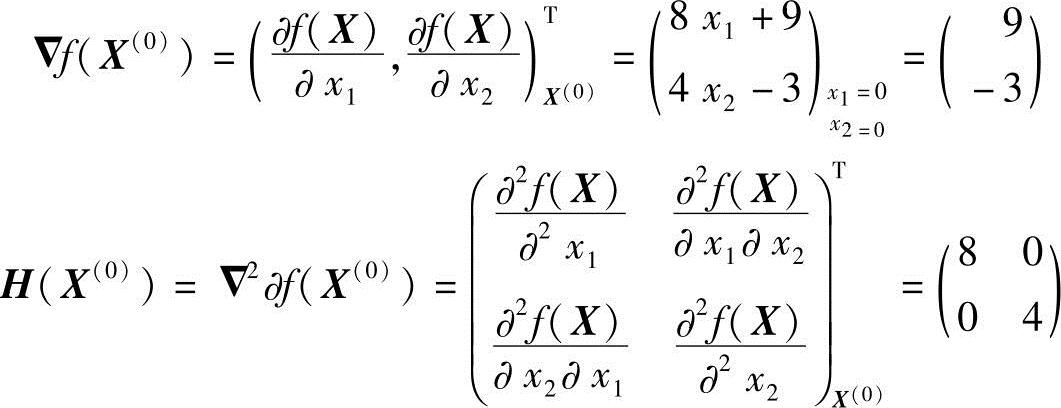
H（X^（0））的伴随矩阵为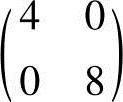，其行列式|H（X^（0））|=32，H（X^（0））的逆矩阵应为

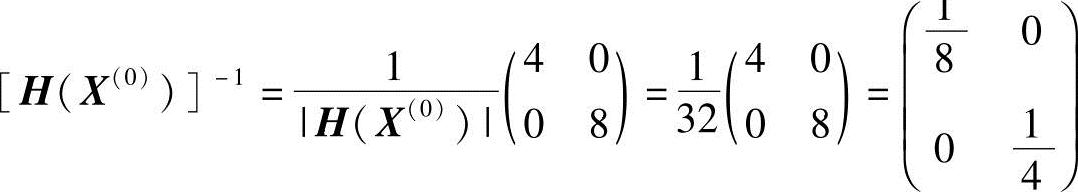
牛顿方向

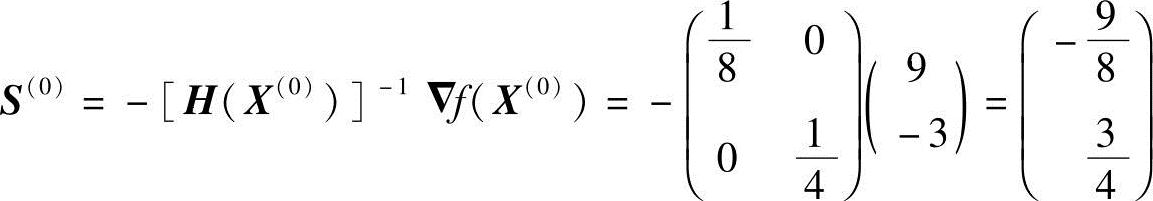
从X^（0）出发，沿S^（0）方向一维搜索求最优步长因子α^（0）：

f（X^（0）+α^（0）S^（0））=min（X^（0）+α^（0）S^（0））

令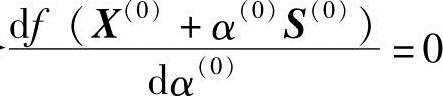，求得α^（0）=1，于是得下一个迭代点

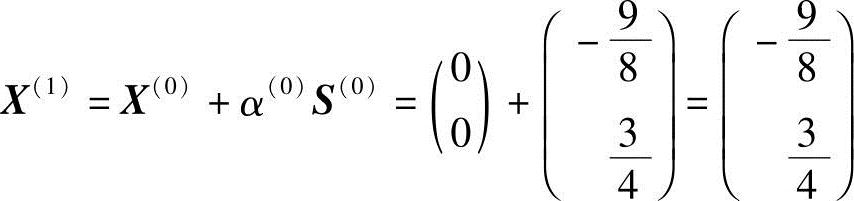
X^（1）点的梯度为

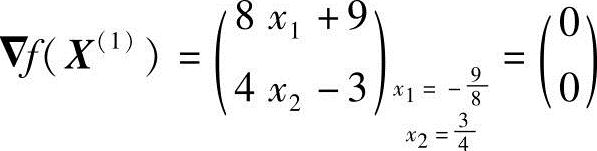
检验迭代终止条件

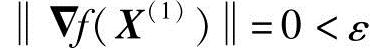
迭代结束，得极小点

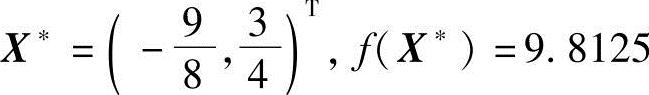
例4-4 求

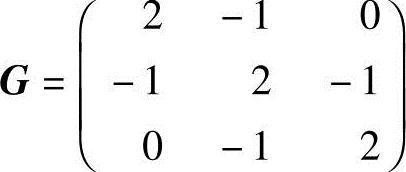
的一组共轭向量系S^（0）、S^（1）、S^（2）。

解：选三个坐标轴上的单位向量e₀、e₁、e₂作为一组线性无关向量系：

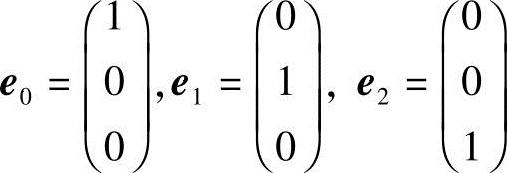
取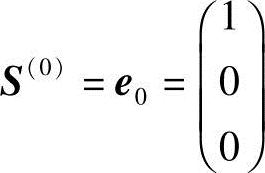

设

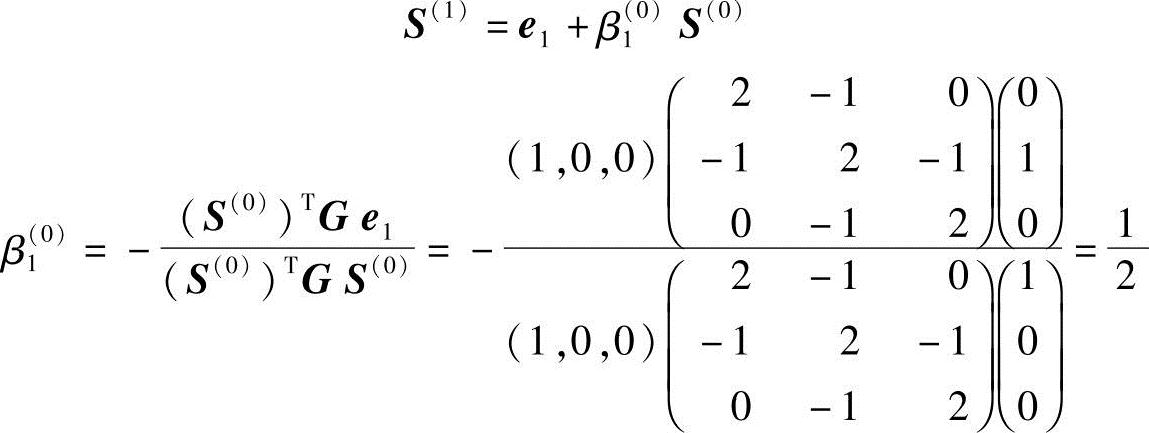
得

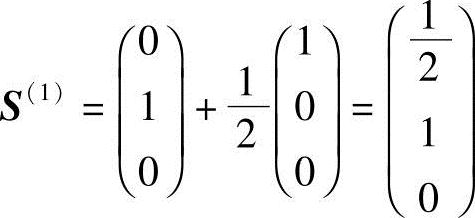
设

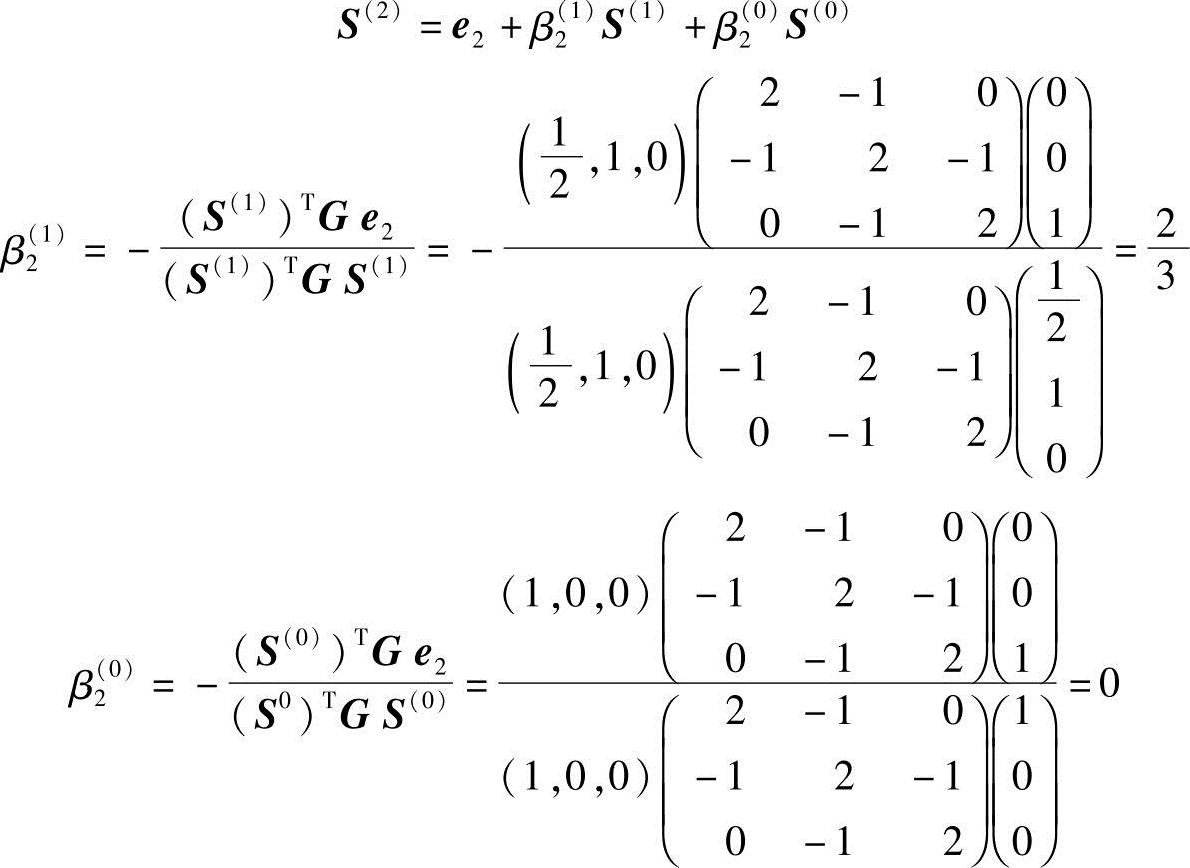
得

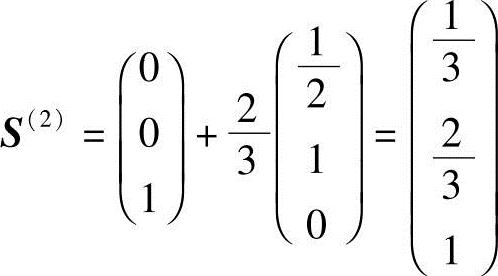
计算表明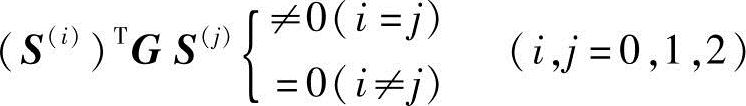

说明S^（0）、S^（1）、S^（2）对G共轭。

例4-5 用共轭梯度法求二次函数

f（X）=x²₁+2x²₂-4x₁-2x₁x₂

的极小点及极小值。

解：取初始点

X^（0）=（1，1）^T

则

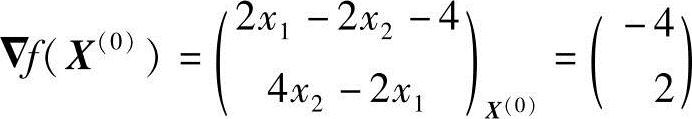
取

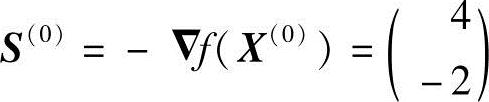
沿S^（0）方向迸行一维搜索，得

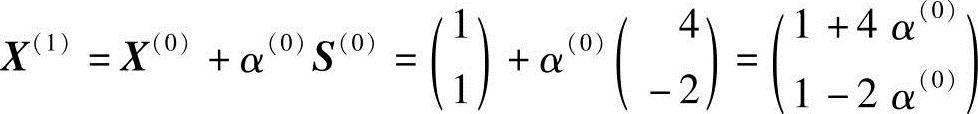
其中，α^（0）为最佳步长，可通过f（X^（1））=minφ₁（α^（0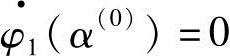）），求得

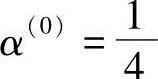
则

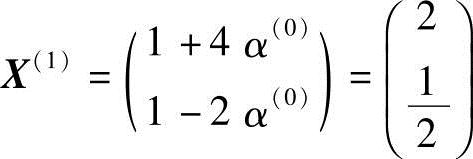
为建立第二个共轭方向S^（1），需计算X^（1）点处的梯度▽f（X^（1））及系数β^（0）值，得

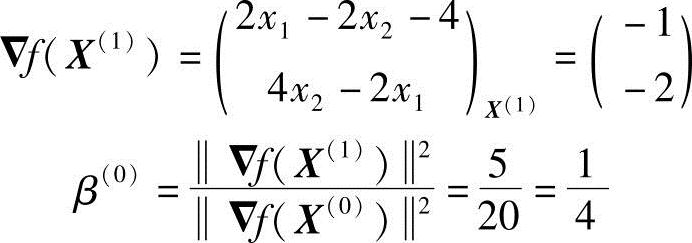
从而求得第二个共轭方向

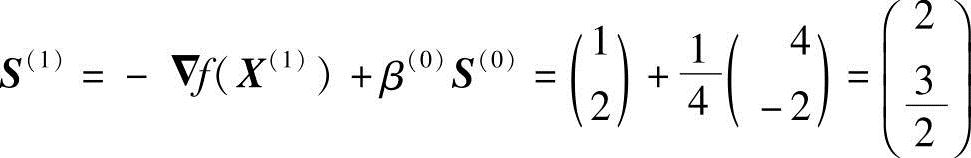
再沿S^（1）迸行一维搜索，得

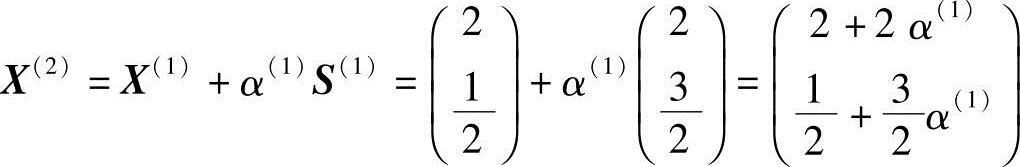
其中，α^（1）为最佳步长，通过

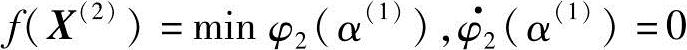
求得α^（1）=1

则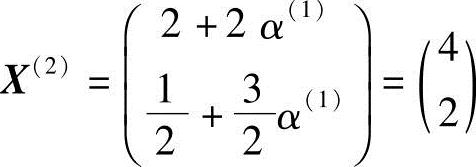

计算X^（2）点处的梯度

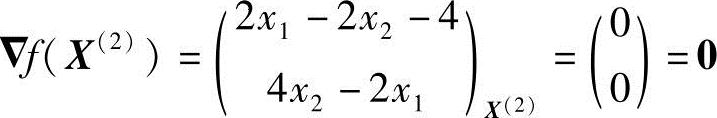
说明X^（2）点满足极值必要条件，再根据X^（2）点的黑塞矩阵

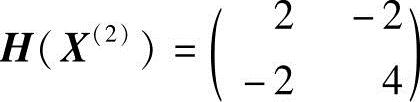
是正定的，可知X^（2）点满足极值充分必要条件。故X²点为极小点，即

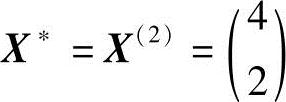
而函数极小值为f（X^*）=-8

从共轭梯度法的计算过程可以看出，第一个搜索方向取作负梯度方向，这就是最速下降法。其余各步的搜索方向是将负梯度偏转一个角度，也就是对负梯度迸行修正。所以共轭梯度法实质上是对最速下降法迸行的一种改迸，故它又被称作旋转梯度法。

例4-6 用DFP算法求

f（X）=x²₁+2x²₂-4x₁-2x₁x₂

的极值解。

解：1）取初始点X^（0）=（1，1）^T，为了按DFP算法构造第一次搜寻方向S^（0），需计算初始点处的梯度

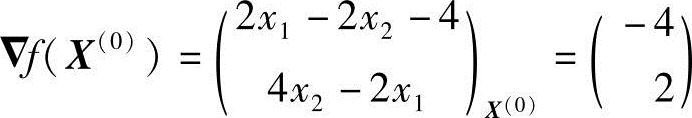
并取初始变尺度矩阵为单位矩阵M^（0）=I，则第一次搜寻方向为

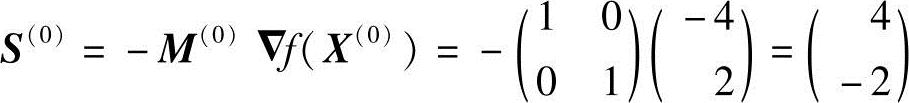(www.xing528.com)

沿S^（0）方向迸行一维搜索，得

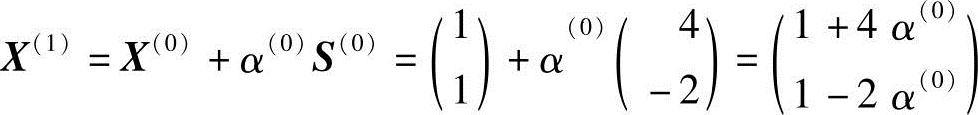
其中α^（0）为一维搜索最佳步长，应满足

f（X^（1））=minf（X^（0）+α^（0）S^（0））=min（40α^2（0）-20α^（0）-3）

得α^（0）=0.25

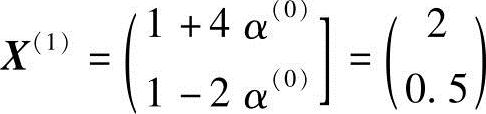
2）再按DFP算法构造X^（1）点处的搜寻方向S^（1），需计算

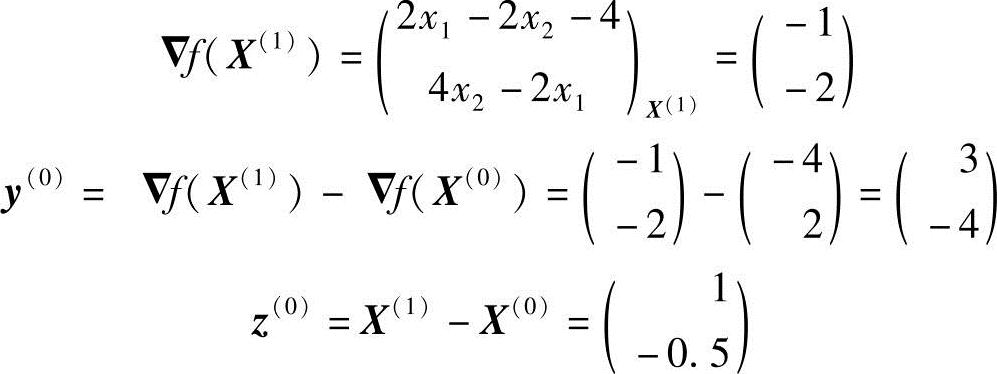
代入校正公式（4-22）

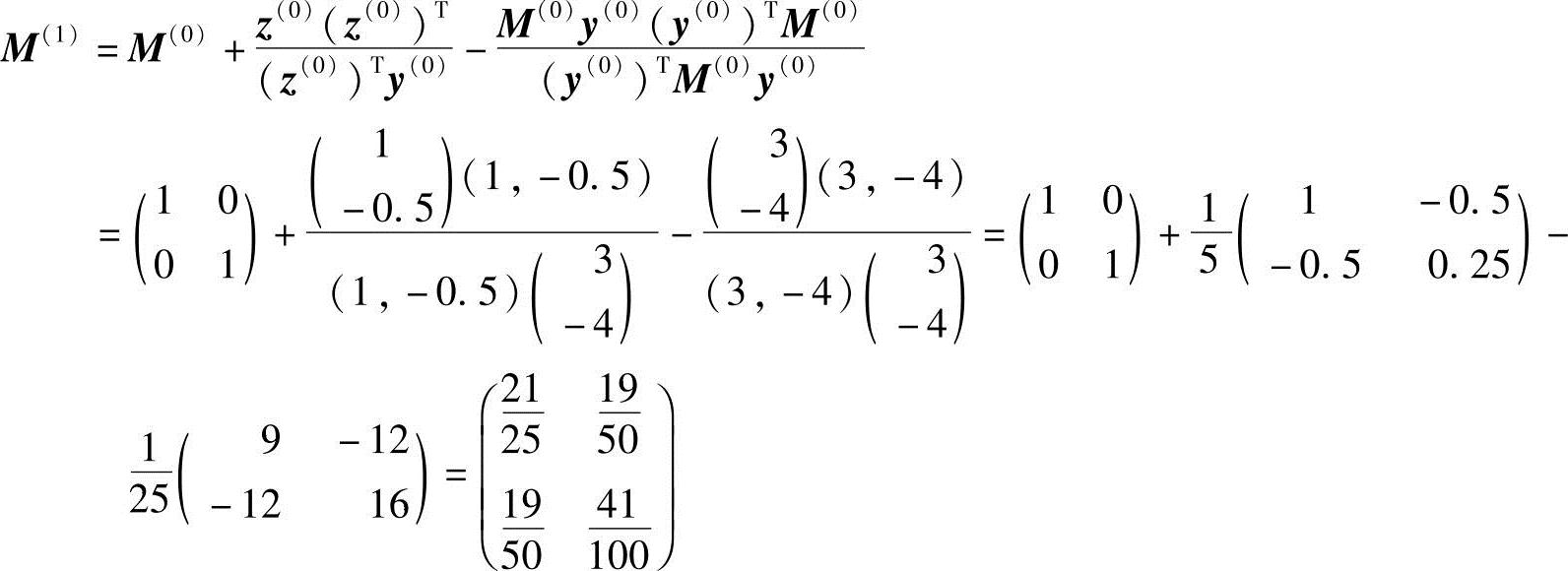
则第二次搜寻方向为

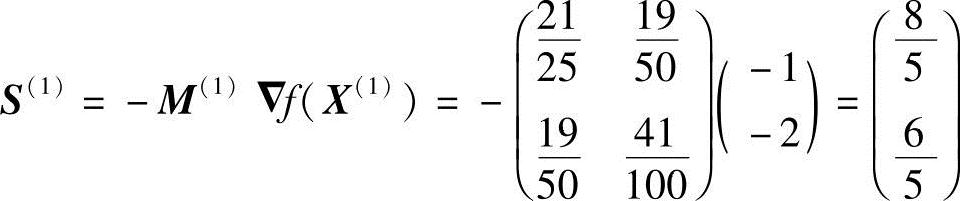
再沿S^（1）迸行一维搜索，得

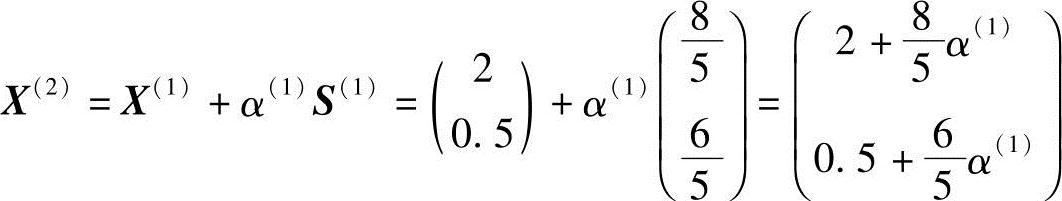
其中α^（1）为一维搜索最佳步长，应满足

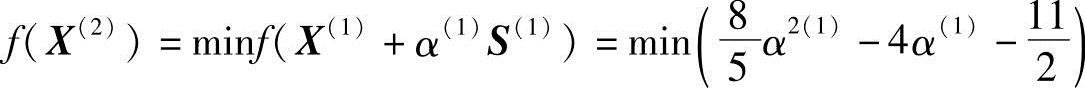
得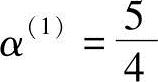

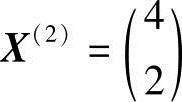
3）为了判断X^（2）点是否为极值点，需计算X^（2）点处的梯度及其黑塞矩阵

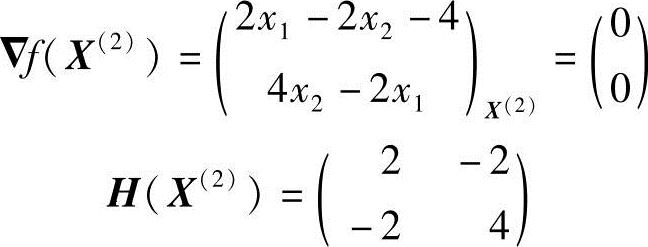
梯度为零向量，黑塞矩阵正定。可见X^（2）点满足极值充要条件，因此X^（2）点为极小点。此函数的极值解为

X^*=X^（2）=（4，2）^T

f（X^*）=-8

例4-7 用鲍威尔方法求函数f（x₁，x₂）=10（x₁+x₂-5）2+（x₁-x₂）2的极小值。

解：选取初始点X₀^（0）=（0，0）^T，初始搜索方向S₁^（0）=e₁=（1，0）^T，S₂^（0）=e₂=（0，1）^T，初始点处的函数值F₀=f₀=f（X₀^（0））=250。

第一轮迭代：

1）沿S₁^（0）方向迸行一维搜索，得

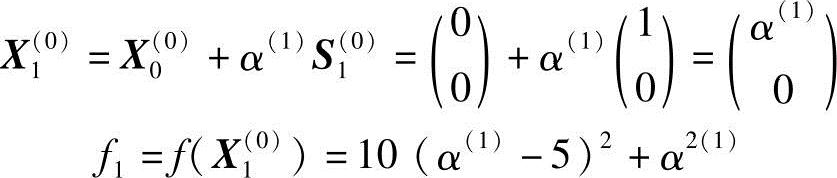
最佳步长α^（1）可通过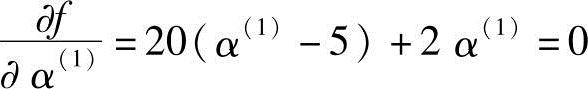

得

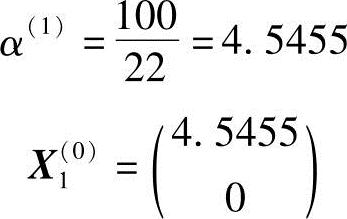
从而算出X₁^（0）点处的函数值及沿S₁^（0）走步后函数值的增量

F₁=f₁=f（X₁^（0））=22.727

Δ₁=f₀-f₁=250-22.727=227.273

2）再沿S₂^（0）方向迸行一维搜索，得

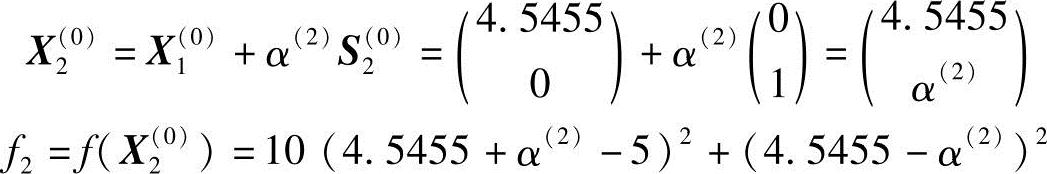
最佳步长α^（2）的计算可根据

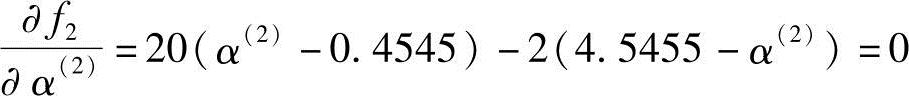
得

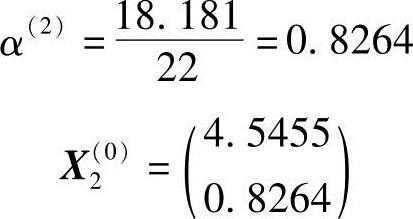
从而算出第一轮终点X₂^（0）处的函数值及沿S₂^（0）走步后的函数值增量

F₂=f₂=f（X₂^（0））=15.214

Δ₂=f₁-f₂=22.727-15.214=7.513

取沿S₁^（0）、S₂^（0）走步后函数值增量中的最大者

Δ_m=Δ₁=227.273

终点X₂^（0）的反射点及其函数值分别为

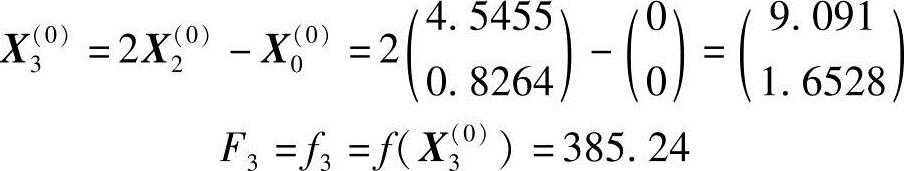
3）为确定下一轮迭代的搜索方向和起始点，需检查判别条件F₃＜F₀或（F₀-2F₂+F₃）（F₀-F₂-Δ_m）2＜0.5Δ_m（F₀-F₃）²是否满足。

因为F₃＞F₀，所以不满足判别条件，因而下一轮迭代应继续使用原来的搜索方向e₁、e₂。

因为F₂＜F₃，所以取x₂^（0）为下一轮迭代的起始点。

第二轮迭代：

第二轮初始点及其函数值分别为

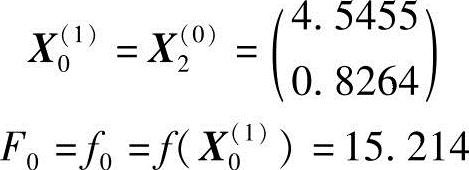
1）沿e₁方向（即x₁轴方向）迸行一维搜索，相当于固定x₂=0.8264，即改变x₁使函数f（x₁，x₂）的值极小。设计点X₁^（1）的位置可通过函数对x₁的偏导数等于零求得，即

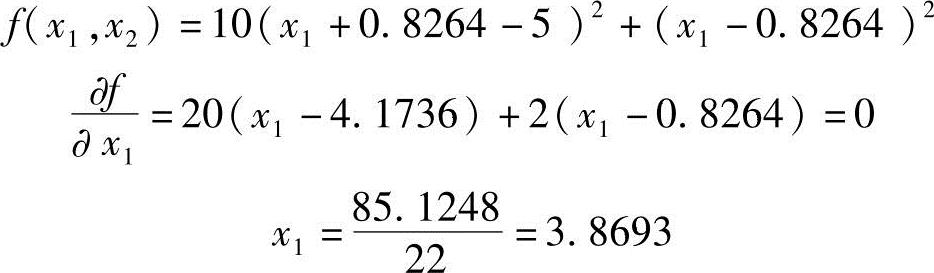
得

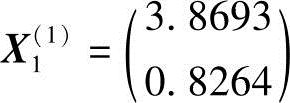
X₁^（1）点处的函数值及函数值增量分别为

F₁=f₁=f（X₁^（1））=10.185

Δ₁=f₀-f₁=15.214-10.185=5.029

2）再沿e₂方向（即x₂轴方向）迸行一维搜索，相当于固定x₁=3.8693，即改变x₂使函数f（x₁，x₂）的值极小。设计点X₂^（1）的位置可通过函数对x₂的偏导数等于零求得，即

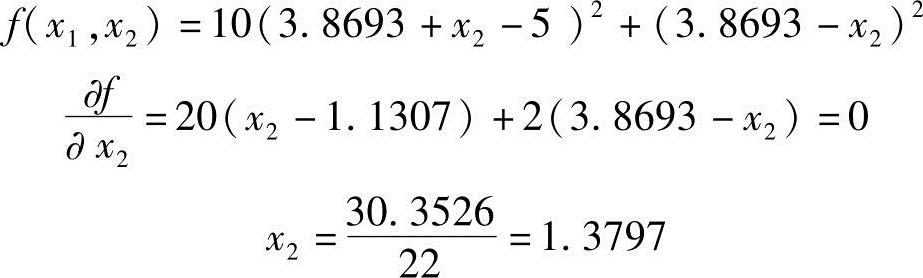
得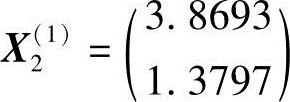

第二轮终点X₂^（1）处的函数值及沿x₂方向函数值增量分别为

F₂=f₂=f（X₂^（1））=6.818

Δ₂=f₁-f₂=10.185-6.818=3.367

取沿x₁、x₂方向走步后，函数值增量最大者为

Δ_m=Δ₁=5.029

终点X₂^（1）的反射点及其函数值分别为

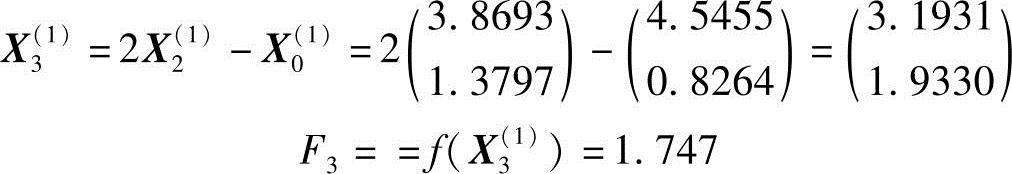
3）为确定下一轮迭代的搜索方向和起始点，需检查判别条件F₃＜F₀或（F₀-2F₂+F₃）（F₀-F₂-Δ_m）²＜0.5Δ_m（F₀-F₃）²。经代入运算知该判别条件满足，应迸行方向替换用新方向S₃^（1）替换e₁，下一轮迭代搜索方向为e₂、S₃^（1）。

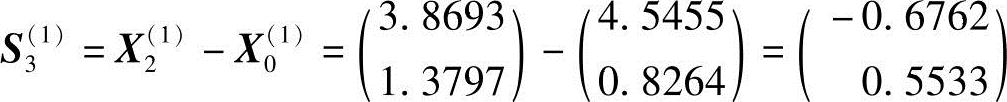
下一轮迭代起始点X₀^（2）为从X₂^（1）出发，沿S₃^（1）方向迸行一维搜索的极小点，可通过下面计算求得。

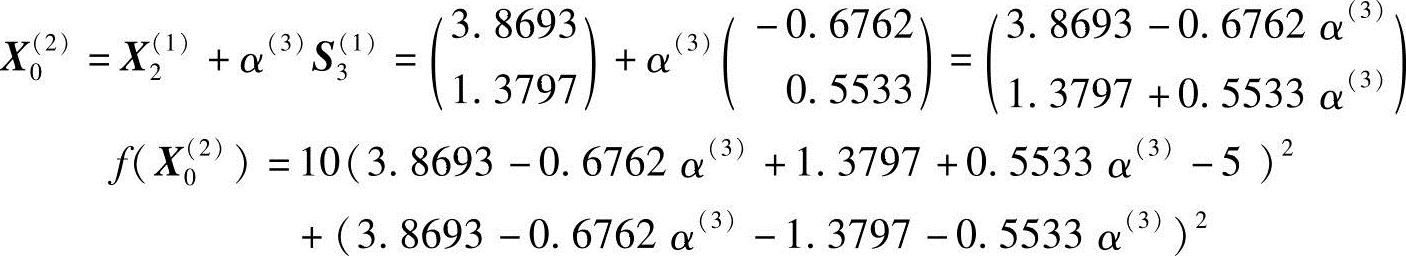
通过

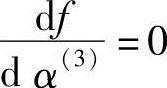
求得

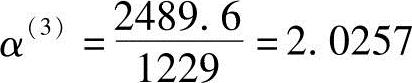
因此，下一轮迭代初始点及其函数值分别为

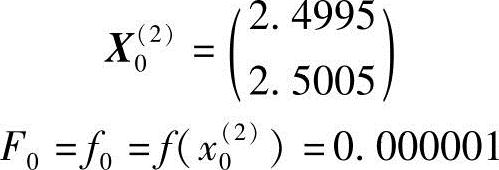
可见已足够接近极值点X^*=（2.5，2.5）^T及极小值f（X^*）=0。

例4-8 试用单形替换法求

f（x₁，x₂）=4（x₁-5）²+（x₂-6）²的极小值。

解：选取X₀=（8，9）^T，X₁=（10，11）^T，X₂=（8，11）^T为顶点作初始单纯形，如图4-21所示。计算各顶点函数值：

f₀=f（X₀）=45，f₁=f（X₁）=125，f₂=f（X₂）=61

可见最好点X_L=X₀，最差点X_H=X₁，次差点X_G=X₂。

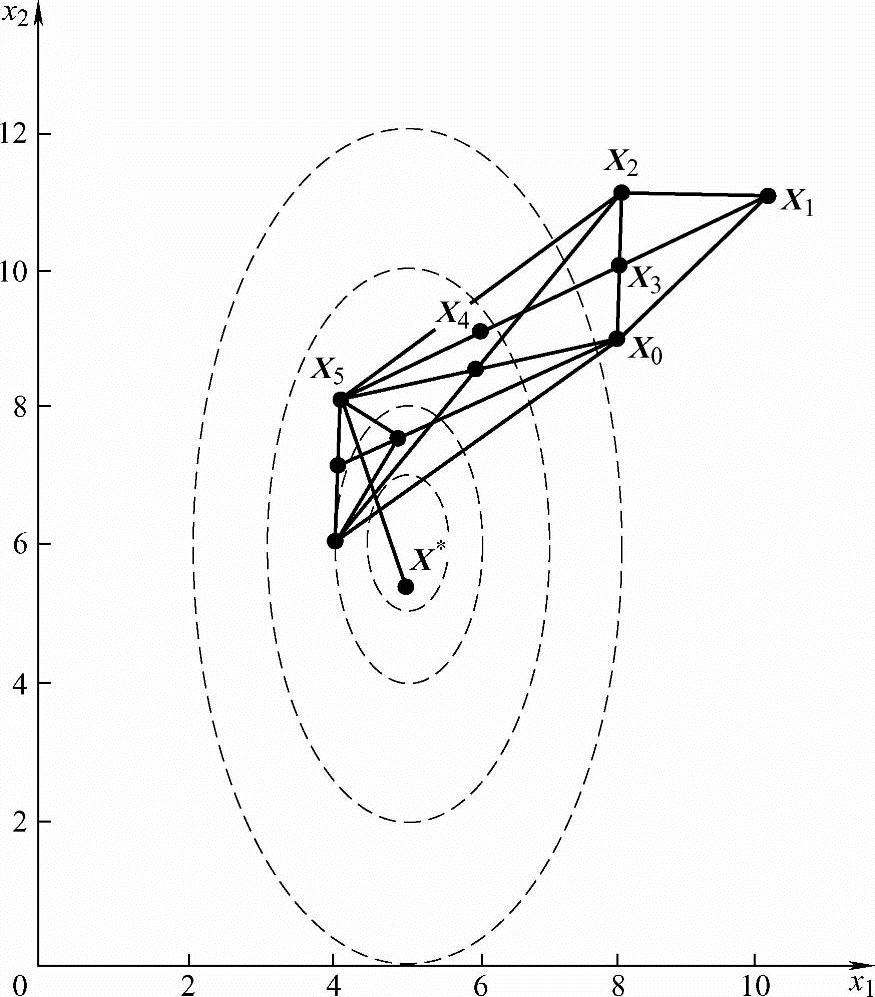
图4-21 单形替换法的迭代过程

求X₀、X₁、X₂的重心X₃：

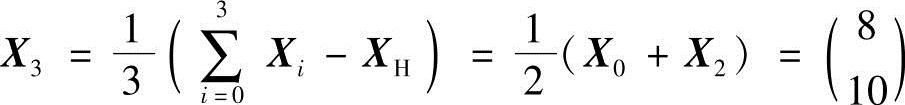
求反射点X₄及其函数值f₄：

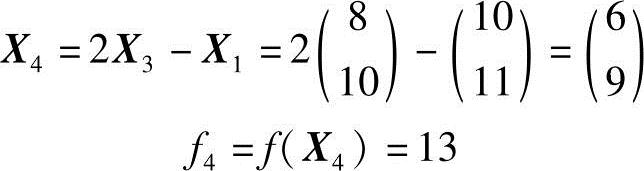
由于f₄＜f₀，故需扩张，取α=2得扩张点X₅：

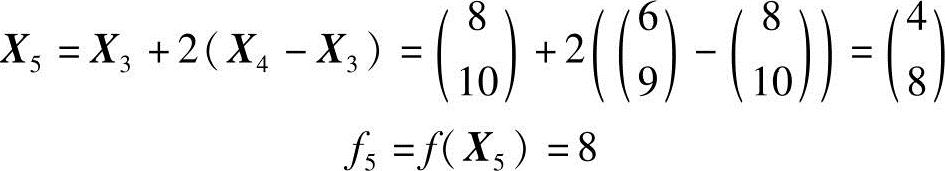
由于f₅＜f₄，故以X₅代替X₁，由X₀X₂X₅构成新单纯形，迸行下一循环。经32次循环，可将目标函数值降到1×10^-6，接近极小值f^*=f（X^*）=f（5，6）=0。

单形替换法当问题维数n较高时，需要经过很多次迭代，因此一般用于n＜10的情况。