将上述对二元函数的处置方法扩展应用到多元函数f(X)中,其计算步骤如下:
1)构造初始单纯形。选初始点X0,从X0出发沿各坐标轴方向走步长h,得n个顶点Xi(i=1,2,…,n)与X0构成初始单纯形。这样可以保证此单纯形各边是n个线性无关的向量,否则就会使搜索范围局限在某个较低维的空间内,有可能找不到极小点。
2)计算各顶点函数值
fi=f(Xi)(i=0,1,2,…,n)
3)比较函数值的大小,确定最好点XL、最差点XH和次差点XG。即有
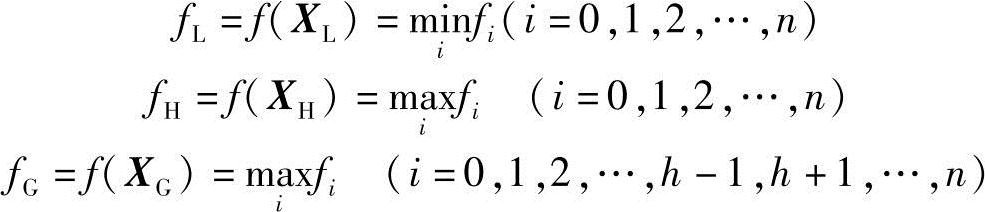
4)检验是否满足收敛准则
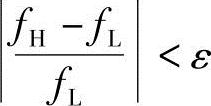
如满足,则X*=XL,结束,否则转5)。
5)计算除XH点之外各点的“重心”Xn+1:

反射点:
Xn+2=2Xn+1-XH
fn+2=f(Xn+2) (4-27)
当fL≤fn+2<fG时,以Xn+2代替XH,fn+2代替fH,构成一新单纯形,然后返回到3)。(https://www.xing528.com)
6)扩张:当fn+2<fL时,取扩张点
Xn+3=Xn+1+α(Xn+2-Xn+1) (4-28)
并计算其函数值fn+3=f(Xn+3)。若fn+3<fn+2,则以Xn+3代替XH,fn+3代替fH,形成一新单纯形;否则,以Xn+2代替XH,fn+2代替fH,形成新单纯形,然后返回到3)。
7)收缩:当fn+2≥fG时则需收缩。如果fn+2<fH,则取收缩点
Xn+4=Xn+1-β(Xn+2-Xn+1)
并计算其函数值fn+4=f(Xn+4);否则,在上式中以XH代替Xn+2,计算收缩点Xn+4及其函数值fn+4。如果fn+4<fH,则以Xn+4代替XH,fn+4代替fH,得新单纯形,返回到3),否则转8)。
8)缩边:将单纯形缩边,可将各向量
Xi-XL(i=0,1,2,…,n)
的长度都缩小一半,即
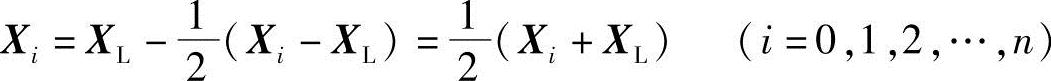
并返回到2)。
单形替换法的程序框图如图4-20所示。
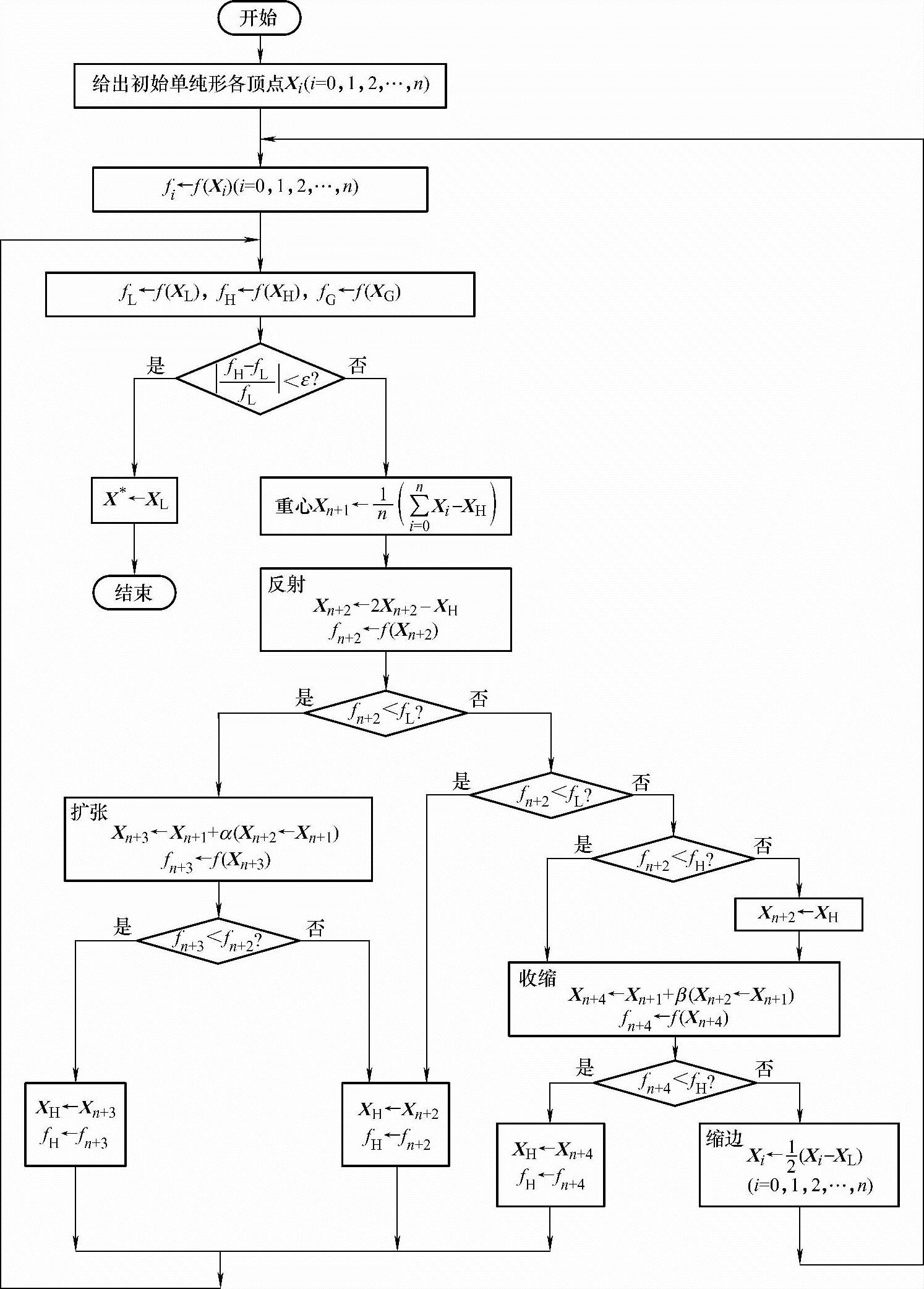
图4-20 单形替换法的程序框图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




