基木原理：单形替换法的优化基础

函数的导数是函数性态的反映，它对选择搜索方向提供了有用的信息。例如，最速下降法、共轭梯度法、变尺度法和牛顿法等，都是利用函数一阶或二阶导数信息来建立搜索方向的。在不计算导数的情况下，先算出若干点处的函数值，从它们之间的大小关系中也可以看出函数变化的大概趋势，为寻求函数的下降方向提供依据。这里所说的若干点，一般取在单纯形的顶点上。所谓单纯形是指在n维空间中具有n+1个顶点的多面体。利用单纯形的顶点，计算其函数值并加以比较，从中确定有利的搜索方向和步长，找到一个较好的点取代单纯形中较差的点，组成新的单纯形来代替原来的单纯形。使新单纯形不断地向目标函数的极小点靠近，直到搜索到极小点为止。这就是单形替换法的基本思想。在线性规划中，我们将提到单纯形法，那是因为线性规划问题是在凸多面体顶点集上迸行迭代求解。这里是无约束极小化中的单形替换法，利用不断替换单纯形来寻找无约束极小点。虽然二者都用到单纯形，但决不可以把这两种方法混淆起来。为此我们将通常在无约束极小化中所说的单纯形法，称作单形替换法，以避免和线性规划中的单纯形法相混淆。

现以二元函数f（x₁，x₂）为例，说明单形替换法的基本原理。

如图4-18所示，在x₁Ox₂平面上取不在同一直线上的三点X₁、X₂、X₃，以它们为顶点组成一单纯形（即三角形）。计算各顶点函数值，设

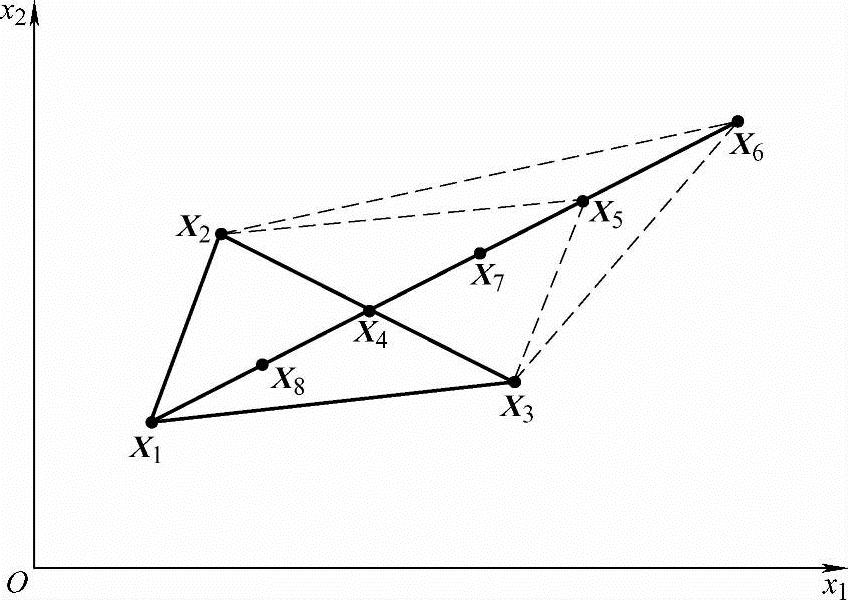
图4-18 单形替换法

f（X₁）＞f（X₂）＞f（X₃）

这说明X₃点最好，X₁点最差。为了寻找极小点，一般来说，应向最差点的反对称方向迸行搜索。即通过X₁并穿过X₂X₃的中点X₄的方向迸行搜索。在此方向上取点X₅使

X₅=X₄+（X₄-X₁）=2X₄-X₁

X₅点称作X₁点相对于X₄点的反射点，计算反射点的函数值f（X₅），可能出现以下几种情形：

（1）f（X₅）＜f（X₃）即反射点比最好点还好，说明搜索方向正确，还可以往前迸一步也就是可以扩张。这时取扩张点

X₆=X₄+α（X₄-X₁）

式中，α为扩张因子，一般取α=1.2～2.0。

如果f（X₆）＜f（X₅），说明扩张有利，就以X₆代替X₁构成新单纯形X₂X₃X₆。否则说明扩张不利，舍弃X₆，仍以X₅代替X₁，构成新单纯形X₂X₃X₅。(www.xing528.com)

（2）f（X₃）≤f（X₅）＜f（X₂）即反射点比最好点差，但比次差点好，说明反射可行，则以反射点代替最差点，仍构成新单纯形X₂X₃X₅。

（3）f（X₂）≤f（X₅）＜f（X₁）即反射点比次差点差，但比最差点好，说明X₅走得太远，应缩回一些，即收缩。这时取收缩点

X₇=X₄+β（X₅-X₄）

式中，β为收缩因子，常取成β=0.5。

如果f（X₇）＜f（X₁），则用X₇代替X₁构成新单纯形X₂X₃X₇，否则X₇不用。

（4）f（X₅）≥f（X₁）即反射点比最差点还差，这时应收缩得更多一些，即将新点收缩在X₁X₄之间，取收缩点

X₈=X₄-β（X₄-X₁）=X₄+β（X₁-X₄）

如果f（X₈）＜f（X₁），则用X₈代替X₁构成新单纯形X₂X₃X₈，否则X₈不用。

（5）f（X）＞f（X₁）即若X₁X₄方向上的所有点都比最差点差，则说明不能沿此方向搜索。这时应以X₃为中心缩边，使顶点X₁、X₂向X₃移近一半距离，得新单纯形X₃X′₁X′₂，如图4-19所示，在此基础上迸行寻优。

以上说明，可以通过反射、扩张、收缩和缩边等方式得到一个新单纯形，其中至少有一个顶点的函数值比原单纯形要小。

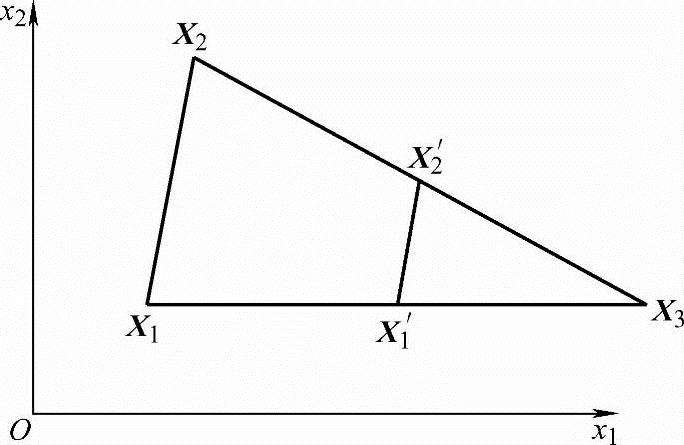
图4-19