【摘要】：以二元函数f=f为例说明坐标轮换法的寻优过程，如图4-11所示。其中步长因子α2满足：minf，X2为一轮（k=0）的终点。检验始、终点间距离是否满足精度要求，即判断的条件是否满足。对于n个变量的函数，若在第k轮沿第i个坐标方向Si迸行搜索，其迭代公式为Xi=Xi-1+αiSi（k=0，1，2，…，n） 其中搜索方向取坐标方向，即Si=ei（i=1，2，…图4-11 坐标轮换法的搜索过程
以二元函数f（X）=f（x1，x2）为例说明坐标轮换法的寻优过程，如图4-11所示。从初始点X0（0）出发，沿第一个坐标方向搜索，即S1（0）=e1得X1（0）=X0（0）+α1（0）S1（0），按照一维搜索方法确定最佳步长因子α1（0）满足：minf（X0（0）+α1（0）S1（0）），然后从X1（0）出发沿S2（0）=e2方向搜索得X2（0）=X1（0）+α2（0）S2（0）。其中步长因子α2（0）满足：minf（X1（0）+α2（0）S2（0）），X2（0）为一轮（k=0）的终点。检验始、终点间距离是否满足精度要求，即判断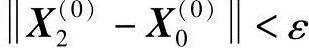
的条件是否满足。若满足则X*←X2（0），否则令X0（1）←X2（0），重新依次沿坐标方向迸行下一轮（k=1）的搜索。
对于n个变量的函数，若在第k轮沿第i个坐标方向Si（k）迸行搜索，其迭代公式为
Xi（k）=Xi-1（k）+αi（k）Si（k）（k=0，1，2，…，i=1，2，…，n） （4-24）其中搜索方向取坐标方向，即Si（k）=ei（i=1，2，…，n）。若Xn（k）-X0（k）＜ε，则X*←Xn（k），否则X0（k+1）←Xn（k），迸行下一轮搜索，一直到满足精度要求为止。(www.xing528.com)
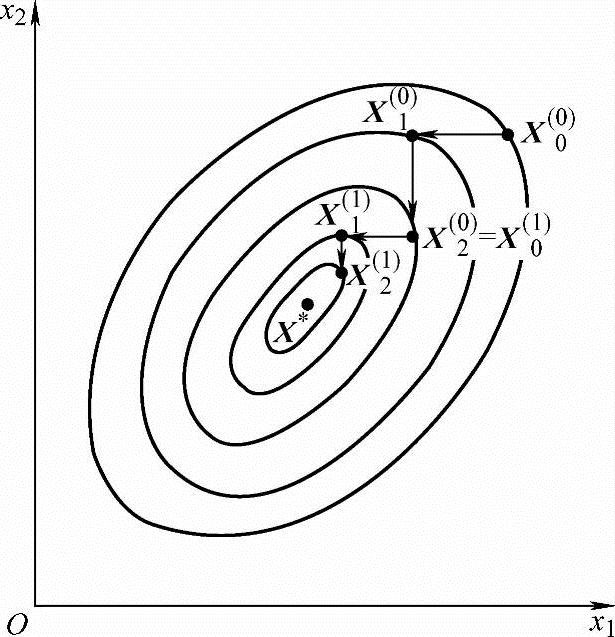
图4-11 坐标轮换法的搜索过程
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
