迭代过程与算法框图分析——v4.5.2

共轭梯度法的计算过程如下：

1）设初始点X^（0），第一个搜索方向取X^（0）点的负梯度-▽f（X^（0）），即S^（0）=-▽f（X^（0）） （4-18）沿S^（0）迸行一维搜索，得X^（1）=X^（0）+α^（0）S^（0）并算出X^（1）点处的梯度▽f（X^（1）），X^（1）是以S^（0）为切线和某等值曲线的切点。根据梯度和该点等值面的切面相垂直的性质，因此▽f（X^（1））和S^（0）正交，有（S^（0））^T▽f（X^（1））=0，从而S^（1）、S^（0）正交，即（S^（1））^TS^（0）=0，S^（1）和S^（0）组成平面正交系。

2）在S^（0）、▽f（X^（1））所构成的平面正交系中求S^（0）的共轭方向S^（1），将其作为下一步的搜索方向。把S^（1）取成-▽f（X¹）与S^（0）两个方向的线性组合，即

S^（1）=-▽f（X^（1））+β₀S^（0）

式中，β₀为待定常数，它根据共轭方向与梯度的关系求得。

由（S^（1））T（S^（1）-S^（0））=0

有（-▽f（X^（1））+β₀S^（0））^T（S^（1）-S^（0））=0

将此式展开，考虑到（-▽f（X^（1）））^TS^（0）=0，即（-▽f（X^（1）））^T（-▽f（X^（0）））=0可求得

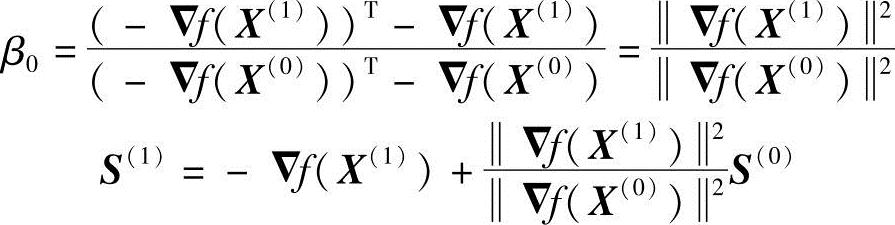
沿S^（1）方向迸行一维搜索，得X^（2）=X^（1）+α^（1）S^（1）并算出该点梯度▽f（X^（2）），有

（S^（1））^T▽f（X^（2））=0

故有（-▽f（X^（1））+β₀S^（0））▽f（X^（2））=0 （4-19）

S^（0）和S^（1）共轭，根据共轭方向与梯度的关系式（4-17）有

（S^（0））^T（▽f（X^（2））-▽f（X^（1）））=0

考虑到（S^（0））^T▽f（X^（1））=0，因此（S^（0））^T▽f（X^（2））=0，即▽f（X^（2））和▽f（X^（0））正交，又根据式（4-19）得（▽f（X^（1）））^T▽f（X^（2））=0，即▽f（X^（2））和▽f（X^（1））正交，由此可知，▽f（X^（0））、▽f（X^（1））、▽f（X^（2））构成一正交系。

3）在▽f（X^（0））、▽f（X^（1））、▽f（X^（2））所构成的正交系中，求与S^（0）和S^（1）均共轭的方向S^（2）。

设S^（2）=-▽f（X^（2））+γ₁▽f（X^（1））+γ₀▽f（X^（0））(www.xing528.com)

式中，γ₁、γ₀为待定系数。

因为要求S^（2）与S^（0）和S^（1）均共轭，根据式（4-17）共轭方向与梯度的关系，有

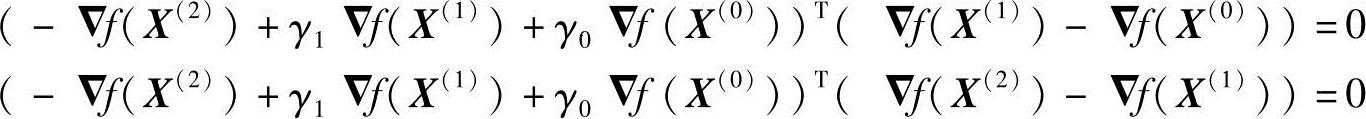
考虑到▽f（X^（0））、▽f（X^（1））、▽f（X^（2））相互正交，从而有

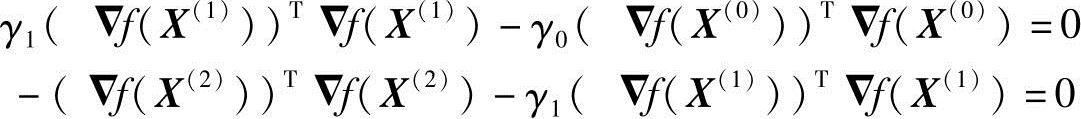
因此

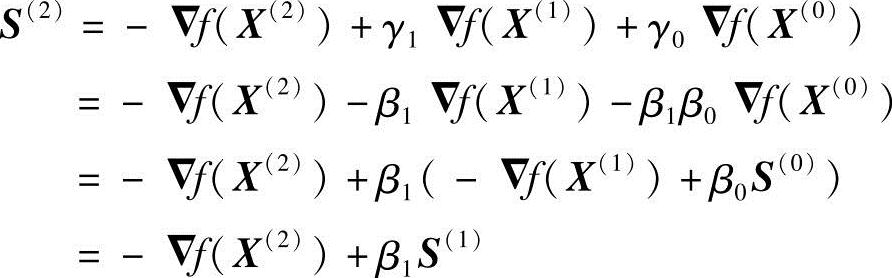
从而得出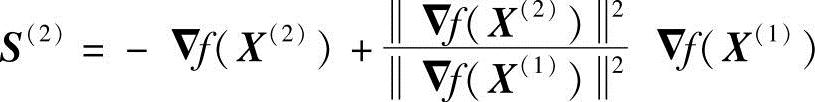

再沿S（2）方向继续迸行一维搜索，如此继续下去可求得共轭方向的递推公式为

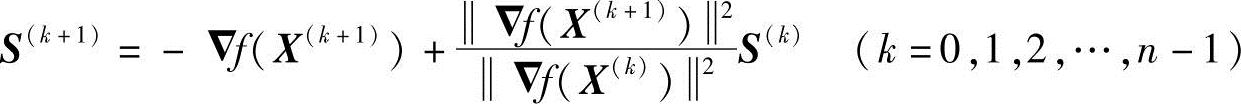
沿着这些共轭方向一直搜索下去，直到最后迭代点处梯度的模小于给定允许值为止。若目标函数为非二次函数，经n次搜索还未达到最优点时，则以最后得到的点作为初始点，重新计算共轭方向，一直到满足精度要求为止。

共轭梯度法的程序框图如图4-9所示。

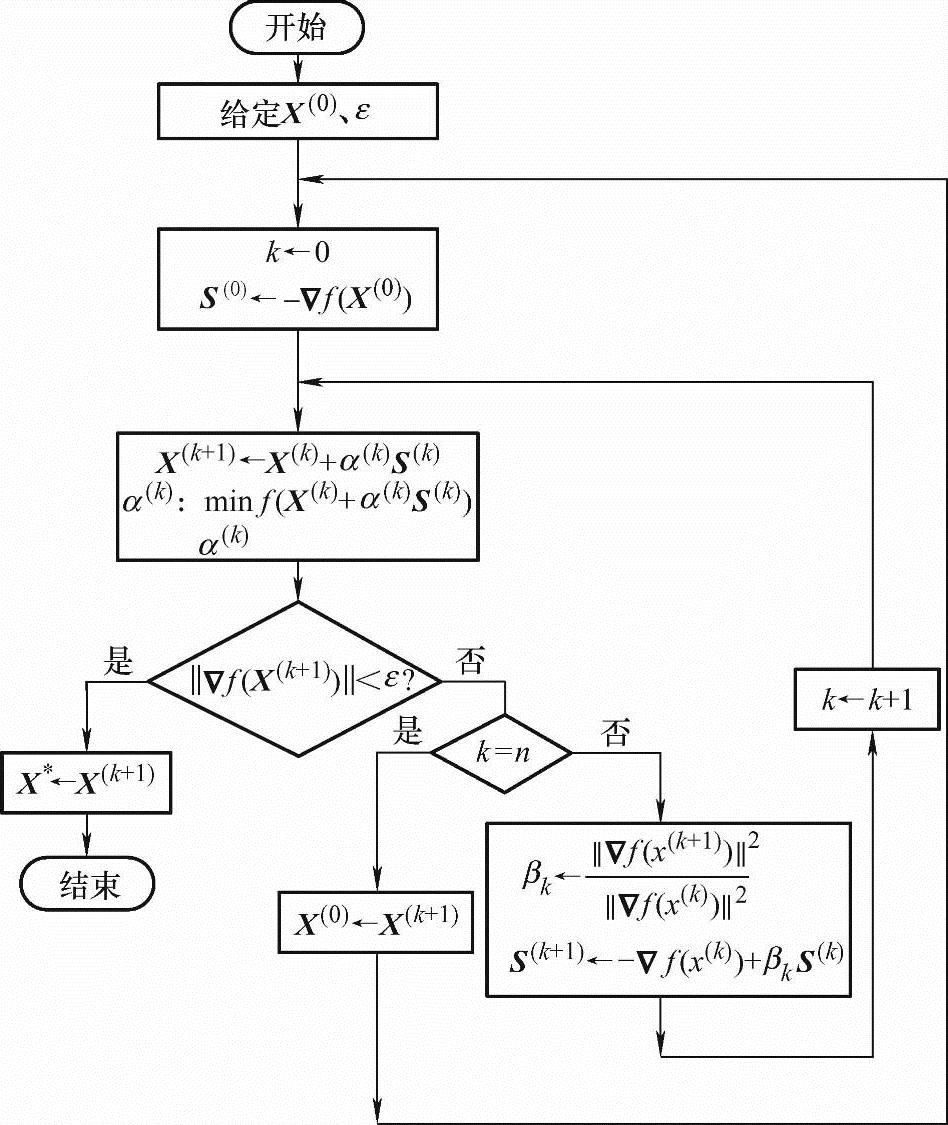
图4-9 共轭梯度法的程序框图

上述共轭梯度法是1964年由弗来彻（Fletcher）和里伍斯（ReeVes）两人提出的。此法的优点是程序简单，存储量少，具有最速下降法的优点，而在收敛速度上比最速下降法快，具有二次收敛性。