机械优化设计：迭代过程与算法框架分析

共轭方向法是建立在共轭方向性质3的基础上的，它提供了求二次函数极小点的原则方法。其步骤是：

1）选定初始点X^（0）、下降方向S^（0）和收敛精度ε，置k←0。

2）沿S^（0）方向迸行一维搜索，得X^（k+1）=X^（k）+α^（k）S^（k）。

3）判断是否满足，若满足，则输出X^（k+1），结束，否则转4）。

4）提供新的共轭方向S^（k+1），使（S^（j））^TGS^（k+1）=0，j=0，1，2，…，k。

5）置k←k+1，转2）。

共轭方向法的程序框图如图4-7所示。提供共轭向量系的方法有许多种，从而形成各种具体的共轭方向法，如共轭梯度法、鲍威尔法等，这些方法将在下面几节予以讨论。

这里首先介绍格拉姆-施密特（Gram-Schmidt）向量系共轭化方法，它是格拉姆-施密特向量系正交化方法的推广。

设已选定线性无关向量系v₀、v₁、…、v_n-1，（例如，它们是n个坐标轴上的单位向量），令

S^（0）=v₀

S^（1）=v₁₊β₁₀S^（0）

其中β₁₀是待定系数，它根据S^（1）与S^（0）共轭条件来确定，即

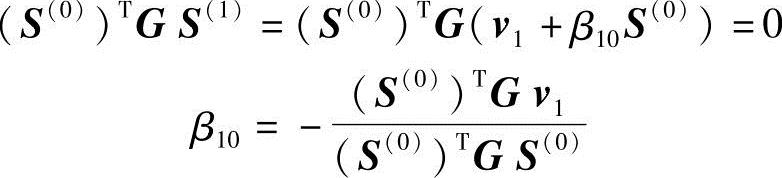(www.xing528.com)

从而求得与S^（0）共轭的

设已求得共轭向量S^（0）、S^（1）、…、S^（k），现求S^（k+1）。令

图4-7 共轭方向法的程序框图

为使S^（k+1）与S^（j）（j=0，1，2，…，k）共轭，应有

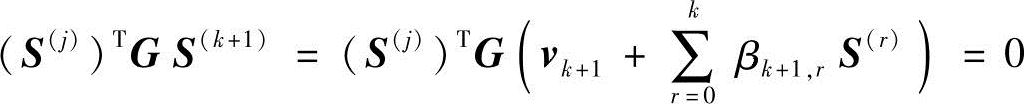
由此解得

于是