基木原理：共轭方向的搜索方法

1.共轭方向的概念

共轭方向的概念是在研究二次函数

（G为对称正定矩阵）时引出的。本节和以后几节所介绍的方法有一个共同的特点，就是首先以式（4-10）的二次函数为目标函数给出有关算法，然后再把算法推广到一般的目标函数中去。

为了直观起见，首先考虑二维情况。二元二次函数的等值线为一族椭圆，任选初始点X^（0）沿某个下降方向S^（0）作一维搜索，得

X^（1）=X^（0）+α^（0）S^（0）

因α^（0）是沿S^（0）方向搜索的最佳步长，即在X^（0）点处函数f^（X）沿S^（0）方向的方向导数为零。

考虑到X^（1）点处方向导数与梯度之间的关系，故有

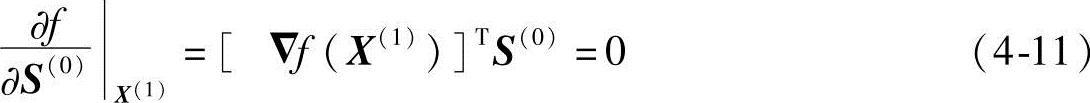
式中，S^（0）与某一等值线相切于X^（1）点。下一次迭代，如果按最速下降法，选择负梯度-▽f（X^（1））方向为搜索方向，则将发生锯齿现象。为避免锯齿的发生，我们可取下一次的迭代搜索方向S^（1）直指极小点X^*，如图4-6所示。如果能够选定这样的搜索方向，那么对于二元二次函数只需顺次迸行S^（0）、S^（1）两次直线搜索就可以求到极小点X^*，即有

X^*=X^（1）+α^（1）S^（1）

式中，α^（1）为S^（1）方向上的最佳步长。

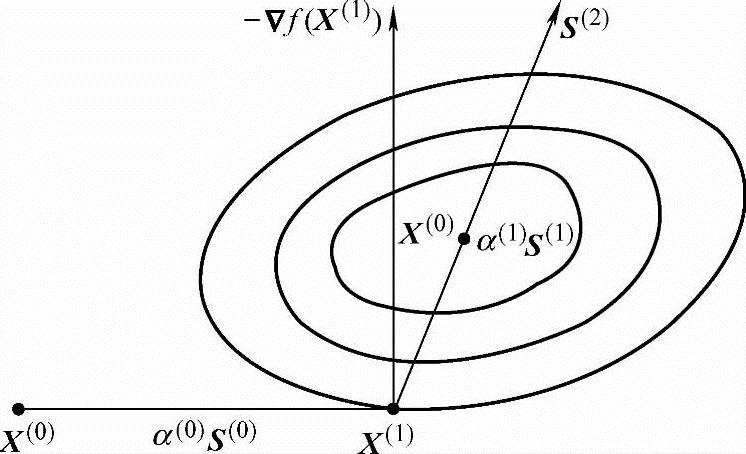
图4-6 共轭方向的搜索方向

那么这样的S^（1）方向应该满足什么条件呢？对于由式（4-10）所表示的二次函数f^（X）有

▽f（X^（1））=GX^（1）+b

当X^（1）≠X^*时，取α^（1）≠0，由于X^*是函数f（X）的极小点，应满足极值必要条件，故有

▽f（X^*）=GX^*+b=0(www.xing528.com)

▽f（X^*）=G（X^（1）+α^（1）S^（1））+b=▽f（X^（1））+α^（1）GS^（1）=0

将等式两边同时左乘（S^（0））^T，并注意到式（4-11）和α^（1）≠0的条件，得

（S^（0））^TGS^（1）=0 （4-12）

这就是为使S^（1）直指极小点X^*、S^（1）所必须满足的条件。满足式（4-12）的两个向量S^（0）、S^（1）称为共轭向量。或称S^（0）、S^（1）是共轭方向。

2.共轭方向的性质

定义 设G为n×n对称正定矩阵，若n维空间中有m个非零向量S^（0）、S^（1）、…、S^（m-1）

满足

（S^（i））^TGS^（j）=0（i，j=0，1，2，…，m-1；i≠j） （4-13）

则称S^（0）、S^（1）、…、S^（m-1）对G共轭，或称它们是G的共轭方向。

当G=I（单位矩阵）时，式（4-13）变成

（S^（i））^TS^（j）=0（i≠j）

即向量S^（0）、S^（1）、…、S^（m-1）互相正交。由此可见，共轭概念是正交概念的推广，正交概念是共轭概念的特例。

性质1 若非零向量系S^（0）、S^（1）、…、S^（m-1）是对G共轭的，则这m个向量是线性无关的。

性质2 在n维空间中互相共轭的非零向量的个数不超过n。

性质3 从任意初始点X^（0）出发，顺次沿G的共轭方向S^（0）、S^（1）、…、S^（m-1）迸行一维搜索，最多经过n次迭代就可以找到由式（4-10）所表示的二次函数f（X）的极小点X^*。

此性质表明这种迭代方法具有二次收敛性。