迭代过程及算法框图解析

二次插值法的计算步骤如下：

1）给定初始区间［a，b]、收敛精度ε和区间中的另外一个点c。

2）将三个已知点按顺序排列：x₁=a，x₂=c，x₃=b，f₁=f（x₁），f₂=f（x₂），f₃=f（x₃）。

3）按式（3-4）或按式（3-5）计算中间插入点x_P及其函数值f_P=f（x_P）。

4）收敛判断：若|x_P-x₂|≤ε，|f₂-f_P|≤ε，则转6）；否则，转5）。

5）缩小区间：

若f_P≤f₂，巨当x_P≤x₂，令x₃=x₂，x₂=x_P，f₃=f₂，f₂=f_P；巨当x_P＞x₂，令x₁=x₂，x₂=x_P，f₁=f₂，f₂=f_P；

若f_P＞f₂，巨当x_P≤x₂，令x₁=x_P，f₁=f_P；巨当x_P＞x₂，令x₃=x_P，f₃=f_P。

转3）求新的插入点。

6）f_P≤f₂，则令x^*=x_P，f^*=f_P；否则，令x^*=x₂，f^*=f₂，结束一维搜索。

二次插值法的区间取舍及替换如图3-10所示，程序框图如图3-11所示。

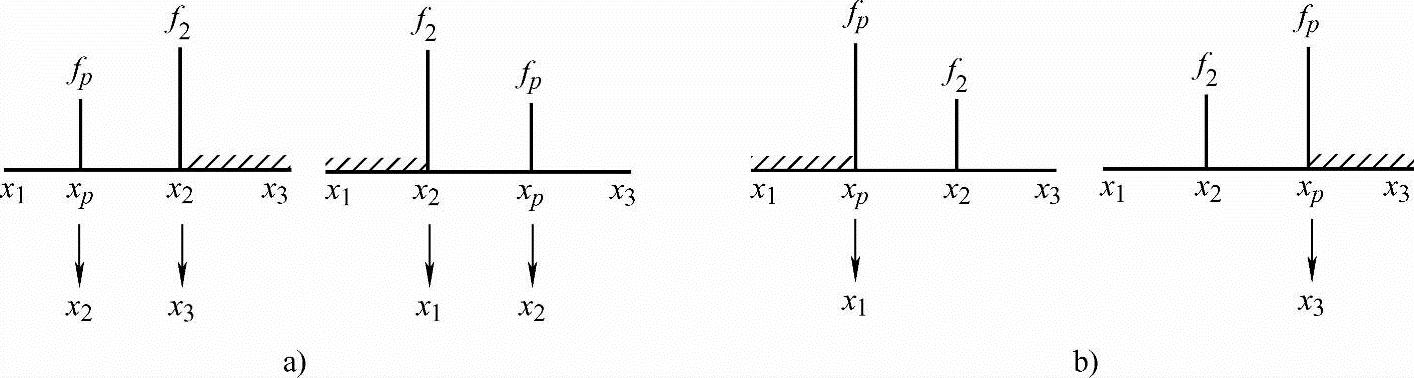
图3-10 二次插值法的区间取舍及替换

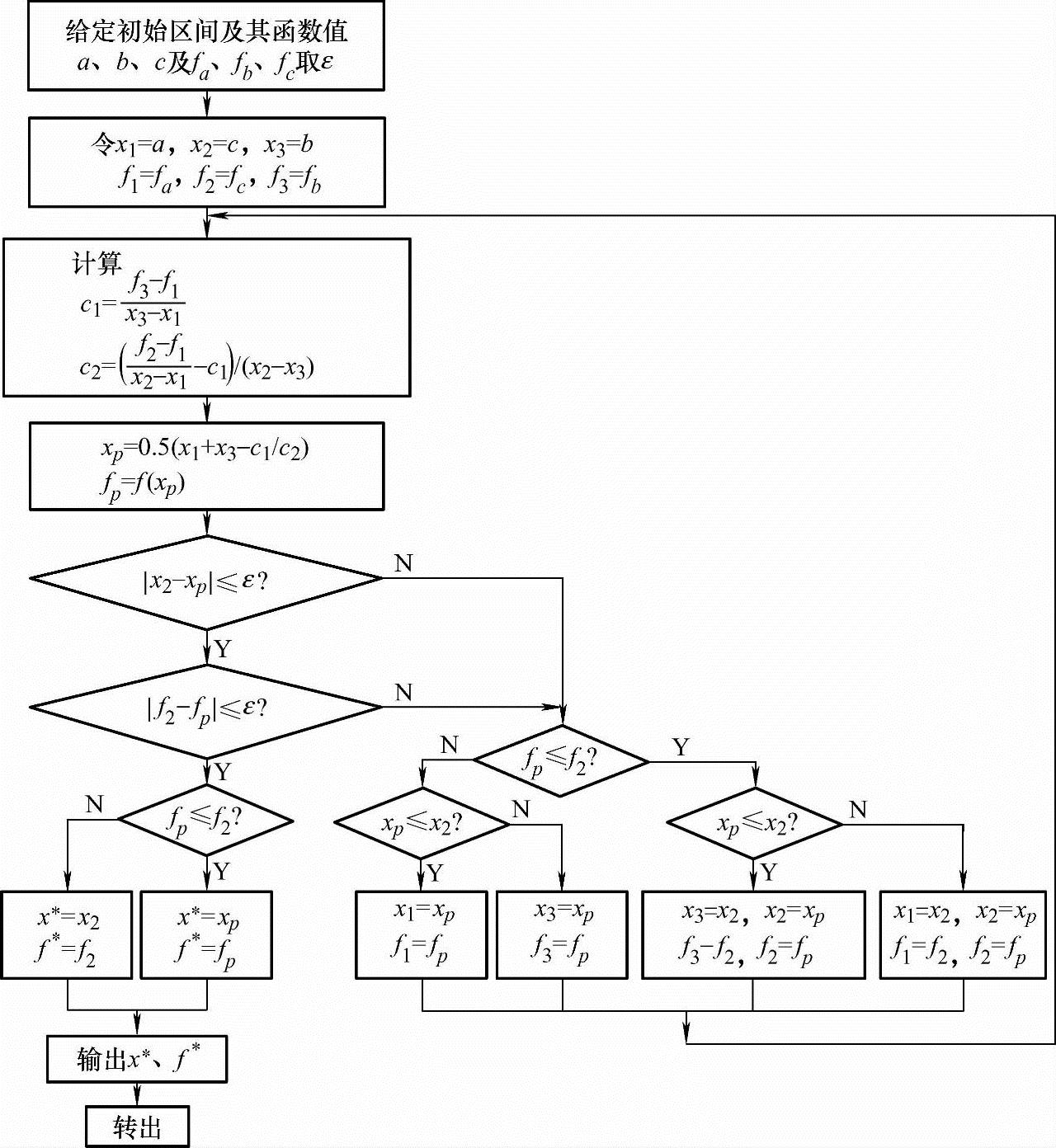
图3-11 二次插值法的程序框图

例3-2 用二次插值法求解例3-1。

解：（1）初始区间的确定(https://www.xing528.com)

初始区间的确定与上题相同。即［a，b]=［0，2]，另有一中间点x₂=1。

（2）用二次插值法接近极小点

1）记此初始区间内的相邻三点及其函数值依次为x₁=0，x₂=1，x₃=2，f₁=2，f₂=1，f₃=18，将它们代入式（3-4），得插值函数的极小点，即新的插入点及其函数值：

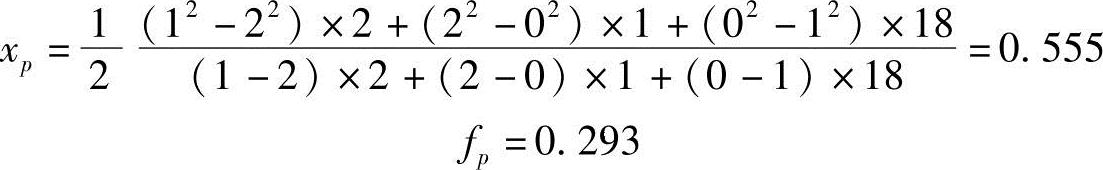
由于f_P＜f₂，x_P＜x₂，故新区间为

［a，b]=［a，x₂]=［0，1]

由于|x₂-x_P|=1-0.555=0.445＞0.2，故应继续做第二次插值计算。

2）在新的区间内，相邻三点及其函数值依次为x₁=0，x₂=0.555，x₃=1，f₁=2，f₂=0.293，f₃=1，将它们代入式（3-4）得

x_P=0.663

f_P=0.222

由于f_P＜f₂，x_P＞x₂，故新区间为

［a，b]=［x₂，b]=［0.555，1]

由于|x₂-x_P|=|0.555-0.663|=0.108＜0.2，故一维搜索到此结束，极小点和极小值分别为

x^*=0.663，f^*=0.222

由以上计算可以看出，二次插值法的收敛速度比黄金分割法快得多。