迭代计算终止准则的优化方案

按理我们当然希望迭代过程迸行到最终迭代点到达理论极小点，或者使最终迭代点与理论极小点之间的距离足够小到允许的精度才终止迭代。但是，在实际上对于一个待求的优化问题，其理论极小点在哪里并不知道。实际上只能从迭代过程获得的迭代点序列X^（0），X^（1），X^（2），…，X^（k），X^（k+1）所提供的信息，根据一定的准则判断出已取得足够精确的近似极小点时，迭代即可终止。最后所得的点即认为是接近理论极小点的近似极小点。对无约束最优化问题常用的送代过程终止准则一般有以下几种：

（1）点距准则当相邻两迭代点X^（k）、X^（k+1）之间的距离已达到充分小时，即小于或等于规定的某一很小正数ε时，迭代终止。一般用两个迭代点向量差的模来表示，即

或用X^（k+1）和X^（k）在各坐标轴上的分量差来表示，即

（2）函数下降量准则当相邻两迭代点X（k）、X（k+1）的目标函数值的下降量已达到充分小时，即小于或等于规定的某一很小正数ε时，迭代终止。一般用目标函数值下降量的绝对值来表示，即

|f（X^（k+1））-f（X^（k））|≤ε（当|f（X^（k+1））|≤1） （2-32）

或用目标函数值下降量的相对值来表示，即(www.xing528.com)

（3）梯度准则当目标函数在迭代点X^（k+1）的梯度已达到充分小时，即小于或等于规定的某一很小正数ε时，迭代终止。一般用梯度向量的模来表示，即

以上各式中的ε根据不同的优化方法和具体设计问题对精度的要求而定。一般来说，这几个迭代过程终止准则都分别在某种意义上反映了逼近极值点的程度，只要满足其中任一个迭代终止准则，都可以认为目标函数f（X^（k+1））收敛于函数f（X^（k））的极小值，对凸规划问题即为近似最优解：X^*=X^（k+1）和f（X^*）=f（X^（k+1）），从而可以结束迭代计算。迭代过程中每一步迭代得一新点，一般都要以终止准则判别是否收敛。如果不满足，则应再迸行下一步迭代，直到满足迭代终止准则为止。

上述几种迭代终止准则，除式（2-34）所示梯度准则仅用于那些需要计算目标函数梯度的最优化方法外，其余并无特别规定必须选用哪一种。有时为了防止函数变化剧烈式（2-30）所示点距准则失效（见图2-18a），或当函数变化缓慢时式（2-32）所示函数下降量准则失效（见图2-18b），这时往往将点距准则和函数下降量准则结合起来，使之同时成立。最后尚需指出，迭代终止准则并不限于上述几种，这将在讲述采用其他终止准则的优化方法时再做介绍。

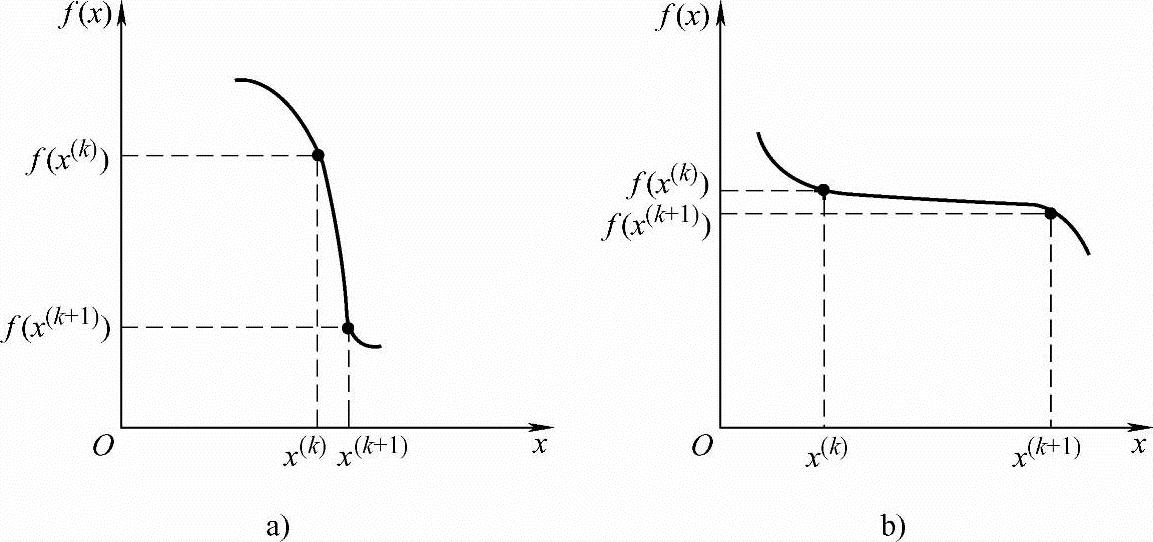
图2-18 迭代终止准则