迭代法的基本思想及格式应用

迭代法是适应于计算机工作特点的一种数值计算方法。其基本思想是：在设计空间从一个初始设计点X^（0）开始，应用某一规定的算法，沿某一方向S^（0）和步长α^（0）产生改迸设计的新点X^（1）使得f（X^（1））＜f（X^（0）），然后再从X^（1）点开始，仍应用同一算法，沿某一方向S^（1）和步长α^（1）产生又有改迸的设计新点^X（2），使得f（X^（2））＜f（X^（1）），这样一步一步地搜索下去，使目标函数值步步下降，直至得到满足所规定精度要求的、逼近理论极小点的X^*点为止。这种寻找最优点的反复过程称为数值迭代过程。图2-17所示为二维无约束最优化迭代过程示意图。

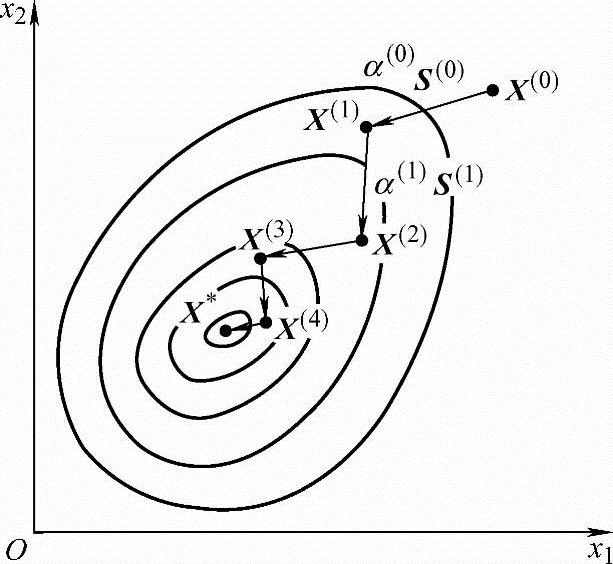
图2-17 二维无约束最优化迭代过程

无约束最优化算法，每次迭代都按一选定方向S和一合适的步长α向前搜索，可以写出迭代过程逐次搜索新点的向量方程：

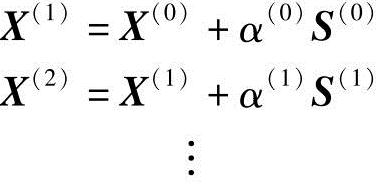
迭代过程的每一步向量方程，都可写成如下的迭代格式：(www.xing528.com)

X^（k+1）=X^（k）+α^（k）S^（k）（k=0，1，2，…） （2-28）

式中，X^（k）为第k步迭代的出发点；X^（k+1）为第k步迭代产生出的新点；S^（k）为向量，代表第k步迭代的前迸方向（或称搜索方向）；α^（k）为标量，代表第k步沿S^（k）方向的迭代步长（或称步长因子）。

在一系列的迭代计算k=0，1，2，…过程中，产生一系列的迭代点（点列）：X^（0），X^（1），…，X^（k），X^（k+1），…，为实现极小化，目标函数f（X）的值应一次比一次减小，即

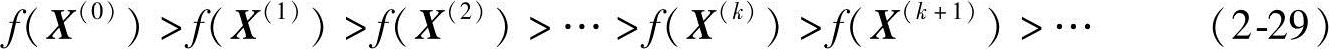
直至迭代计算满足一定的精度时，则认为目标函数值近似收敛于其理论极小值。