在约束条件下求得的函数极值点,称为约束极值点。在优化实用计算中常需判断和检查某个可行点是否为约束极值点,这通常借助于库恩-塔克(Kuhn-Tucker)条件(简称K-T条件)来迸行。
K-T条件可阐述为:如果X(k)是一个局部极小点,则该点的目标函数梯度▽f(X(k))可表示成该点诸约束面梯度▽gu(X(k))、▽hv(X(k))如下线性组合:
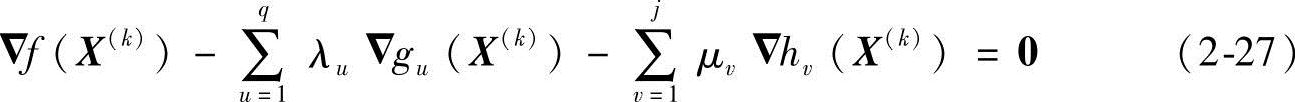
式中,q为在X(k)点的不等式约束面数;j为在X(k)点的等式约束面数;λu(u=1,2,…,q)、μv(v=1,2,…,j)均为非负值的乘子,亦称拉格朗日乘子。如果无等式约束,而全部是不等式约束,则式(2-27)中j=0,第三项全部为零。
也可以对K-T条件用图形来说明。式(2-27)表明,如果X(k)是一个局部极小点,则该点的目标函数梯度▽f(X(k))应落在该点诸约束面梯度▽gu(X(k))、▽hv(X(k))在设计空间所组成的锥角范围内。如图2-11所示,图2-11a中设计点X(k)不是约束极值点,图2-11b中的设计点X(k)是约束极值点。
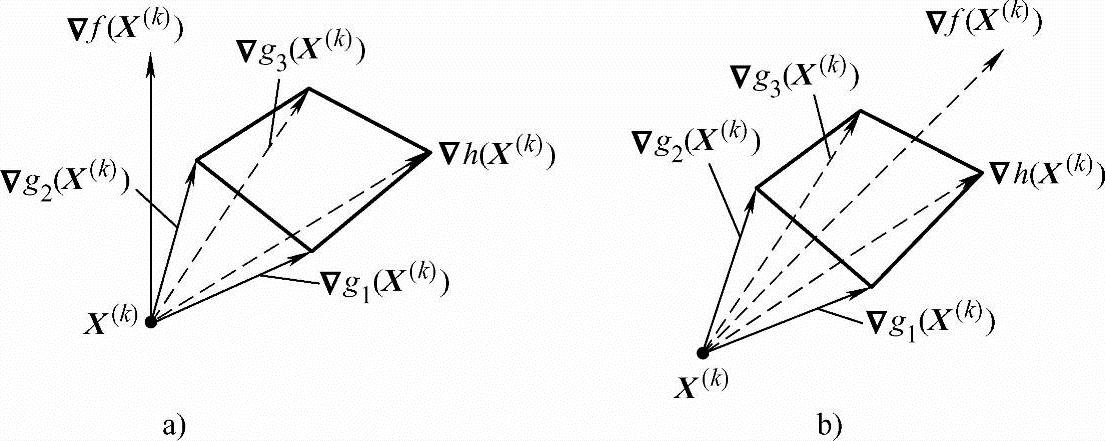
图2-11 K-T条件的几何意义
以二维情况为例,将更形象地表明K-T条件。
图2-12所示为在设计点X(k)处有两个约束,图2-12a表示X(k)点处目标函数梯度▽f(X(k))在该点两个约束函数梯度▽g1(X(k))、▽g2(X(k))组成的锥角Γ以外,这样在X(k)点邻近的可行域内存在目标函数值比f(X(k))更小的设计点,故X(k)点不能成为约束极值点;而图2-12b表示X(k)点处▽f(X(k))落在锥角Γ以内,则在该点附近邻域内任何目标函数值比f(X(k))更小的设计点都在可行域以外,因而X(k)是约束极值点,它满足式(2-27)所示K-T条件
▽f(X(k))-λ1▽g1(X(k))-λ2▽g2(X(k))=0(λ1≥0,λ2≥0)
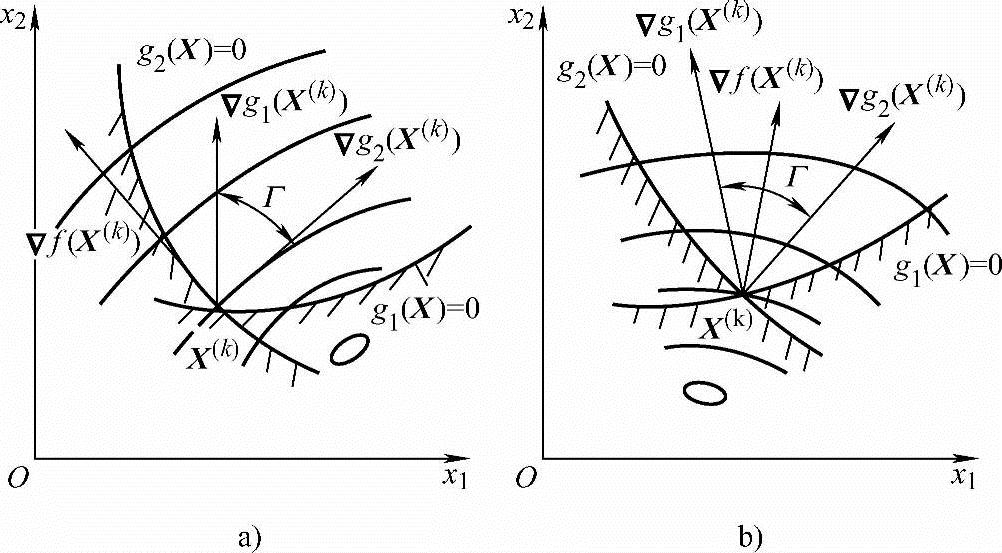
图2-12 二维函数K-T条件图解
图2-13所示为在设计点X(k)处只有一个约束,图2-13a表示▽f(X(k))和▽g(X(k))的方向不重合,在X(k)邻近的可行域内存在目标函数值比f(X(k))更小的设计点,故X(k)不能成为约束极值点;而图2-13b中由于▽f(X(k))和▽g(X(k))的方向重合,则-▽f(X(k))-λ▽g(X(k))=0,λ>0,此即当X(k)点处约束面数q=1时的K-T条件,显然X(k)点附近邻域内任何目标函数值比f(X(k))更小的设计点都在可行域以外,X(k)点是约束极值点。
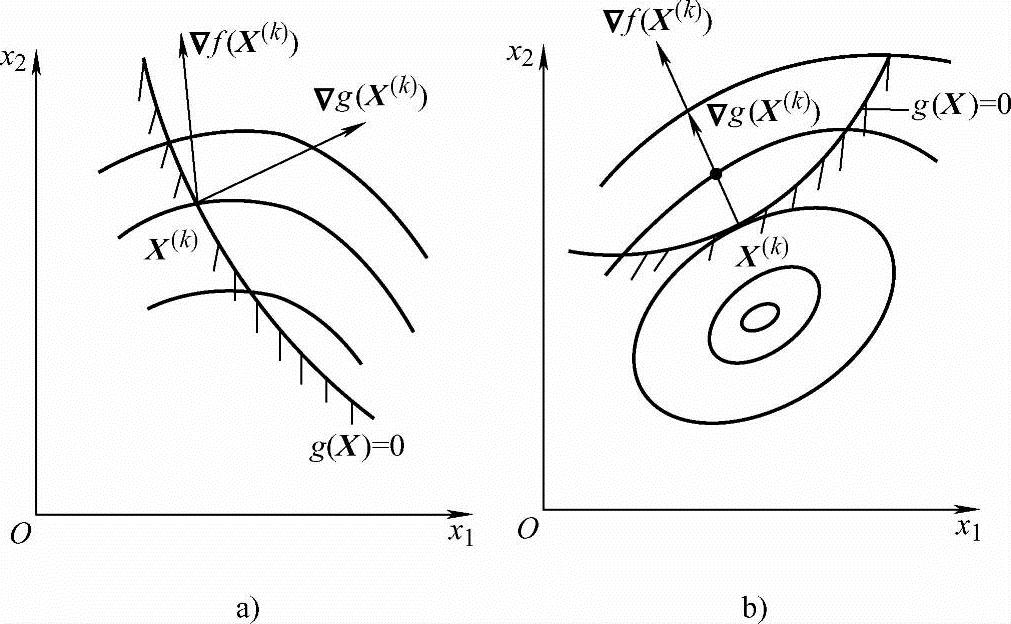
图2-13 约束极值点存在的条件
必须指出,K-T条件用于检验设计点是否为约束极值点,对于“凸规划”问题,即对于目标函数f(X)为凸函数、可行域为凸集的优化问题,局部极值点与全域最优点相重合,如图2-12b、图2-13b皆为凸规划问题,X(k)点符合K-T条件,必为全域最优点,但对于非凸规划问题则不然。图2-14a所示是目标函数为非凸函数、约束可行域为凸集,图2-14b所示是目标函数为凸函数、约束可行域为非凸集,这两种情况在可行域中均可能出现两个或更多的局部极小点,它们必须都满足K-T条件;但其中只有一个函数值最小的点X(k)是约束最优点。在工程优化设计问题中函数在全域上的凸性不一定存在,在许多情况下,凸性的判断亦难迸行。因此判断符合K-T条件的约束极值点是全域最优点还是局部极值点目前仍是优化研究的一个重大课题。但凸集、凸函数、K-T条件等在优化理论和实践中仍具有重要意义。亦须指出,用K-T条件检验约束极值点是指具有起作用约束的可行点。如图2-15所示,无约束极值点X*处gu(X*)均大于零(u=1,2,3,4),这一约束条件对X*都不起作用,X*亦是约束极值点,但却不属于K-T条件的范围。
例2-3 用K-T条件检验点X(k)=(2,0)T是否为目标函数f(X)=(x1-3)2+x22+5在不等式约束:g1(X)=4-x21-x2≥0、g2(X)=x2≥0、g3(X)=x1-0.5≥0条件下的约束最优点。
解:(1)计算X(k)点的诸约束函数值(https://www.xing528.com)
g1(X(k))=4-22-0=0
g2(X(k))=0
g3(X(k))=2-0.5=1.5>0
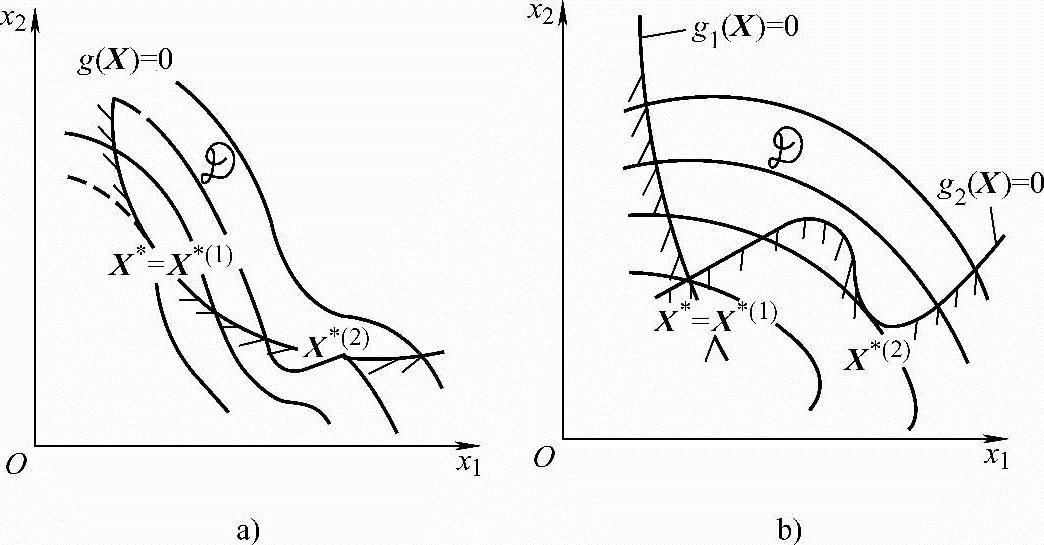
图2-14 非凸集定义域凸函数极值存在情况
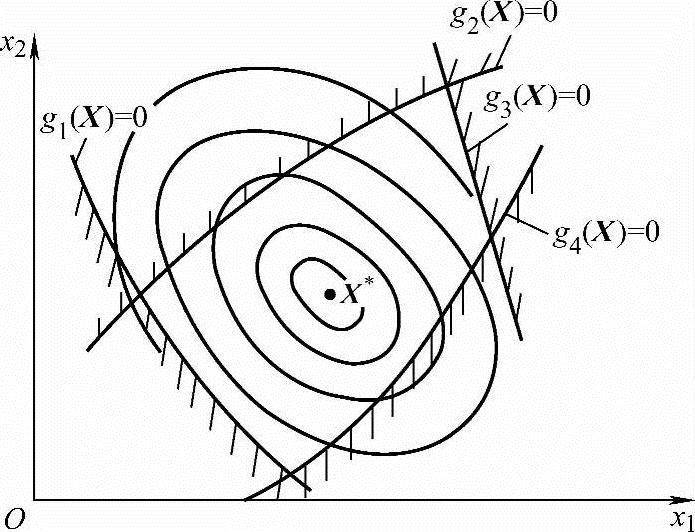
图2-15 不属于K-T条件的约束极值点
X(k)点是可行点,该点起作用的约束函数是g1(X)、g2(X)。
(2)求X(k)点的有关诸梯度
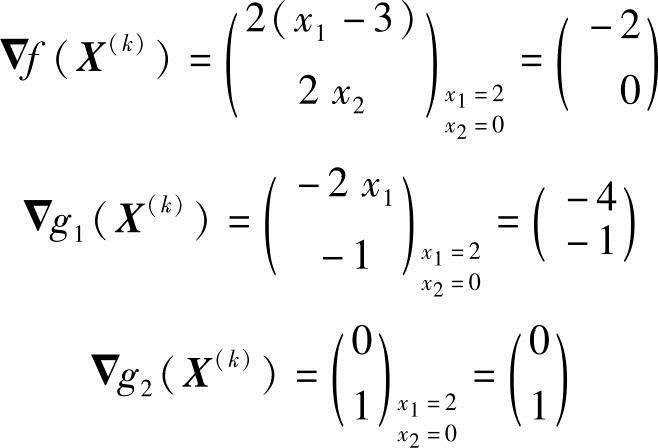
(3)代入式(2-27),求拉格朗日乘子
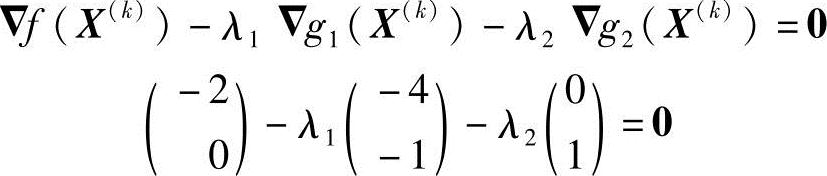
写成线性方程组
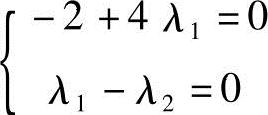
解得λ1=λ2=0.5,乘子均为非负,故满足K-T条件,即X(k)=(2,0)T点为约束极值点。参看图2-16,亦得到证实。而巨,由于f(X)是凸函数,可行域为凸集,所以点X(k)=(2,0)T也是约束最优点。
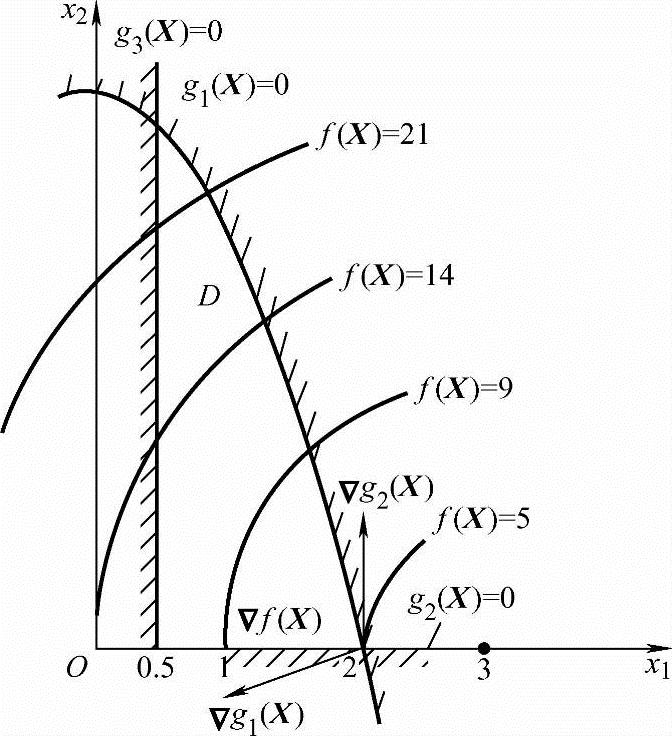
图2-16 例2-3图解
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




