机械优化设计：等式约束极值点条件

求解等式约束优化问题：

minf（X）

s.t.h_k（X）=0（k=1，2，…，m）

需要导出极值存在的条件，这是求解等式约束优化问题的理论基础。对这一问题在数学上有两种处理方法：消元法（降维法）和拉格朗日乘子法（升维法），现分别予以介绍。

1.消元法

为了便于理解，先讨论二元函数只有一个等式约束的简单情况，即

minf（x₁，x₂）

s.t.h（x₁，x₂）=0

根据等式约束条件将一个变量x₁表示成另一个变量x₂的函数关系x₁=φ（x₂），然后将这一函数关系代入到目标函数f（x₁，x₂）中消去x₁，变成一元函数F（x₂），从而将等式约束优化问题转化成无约束优化问题。目标函数通过消元由二元函数变成一元函数，即由二维变成一维。所以消元法又称作降维法。

对n维情况

minf（x₁，x₂，…，x_n）

s.t.h_k（x₁，x₂，…，x_n）=0（k=1，2，…，l）

由l个约束方程将n个变量中的前l个变量用其余n-l个变量表示，即有

x₁=φ₁（x₁₊₁，x₁₊₂，…，xn）

x₂=φ₂（x_l+1，x₁₊₂，…，xn）

…

x_l=φl（x_l+1，x_l+2，…，xn）

将这些函数关系代入到目标函数中，从而得到只含x_l+1，x_l+2，…，x_n共n-l个变量的函数，这样就可以利用无约束优化问题的极值条件求解。

消元法虽然看起来简单，但是实际求解困难却很大。因为将l个约束方程联立往往求不出解来。即使能求出解，当把它们代入目标函数之后，也会因为函数十分复杂而难以处理。所以，以这种方法作为一种分析方法实用意义不大，而对某些数值迭代方法来说，却有很大的启发意义。

2.拉格朗日乘子法

拉格朗日乘子法是求解等式约束优化问题的另一种经典方法，它是通过增加变量将约束优化问题变成无约束优化问题，所以又称作升维法。

对于具有l个等式约束的n维优化问题

minf（X）

s.t.h_k（X）=0（k=1，2，…，l）

在极值点X*处有

把l个等式约束给出的l个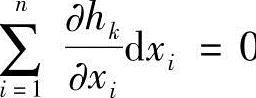0，分别乘以待定系数λ_k（k=1，2，…，l）再和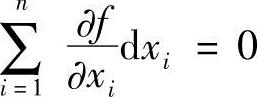相加，得(www.xing528.com)

可以通过其中的l个方程

来求解l个λ₁，λ₂，…，λ_l，使得l个变量的微分dx₁，dx₂，…，dx_l的系数全为0，这样，式（2-20）的等号左边就只剩下n-l个变量的微分dx_l+1，dx_l+2，…，dx_n的项，即它变成

但dx_l+1，dx_l+2，…，dx_n应是任意量，则应有

式（2-22）和式（2-23）及等式约束h_k（X）=0（k=1，2，…，l）就是点X达到约束极值的必要条件。

式（2-21）和式（2-23）可以合并写成

根据目标函数f（X）的无约束极值条件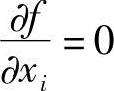（i=1，2，…，n），则上述问题的约束极值条件可以转换成无约束的函数极值条件。办法是，把原来的目标函数f（X）改造成为如下形式的新目标函数：

式中的h_k（X）就是原目标函数f（X）的等式约束条件，而待定系数λ_k称为拉格朗日乘子，F（X，λ）称为拉格朗日函数。这种方法称为拉格朗日乘子法。

式（2-25）中显然多出了l个待定系数λ_k（可看成是新的变量），而X=（x₁，x₂，…，x_n）T有n个变量。结果共有n+l个变量。但是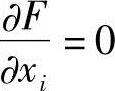可提供n个方程，再加上l个等式约束条件h_k（X）=0，共有n+l个方程，足以解出这n+l个变量。

由于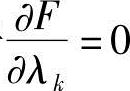给出h_k（X）=0，所以这n+l个方程可以看成是通过下述条件给出的：

这样，拉格朗日乘子法可以叙述如下：

设X^*是目标函数f（X）在等式约束h_k（X）=0条件下的一个局部极值点，而巨在该点处函数的梯度▽h_k（X^*）=0（k=1，2，…，l）是线性无关的，则存在一个向量λ（在l个约束函数规定的集内），使得下式成立：

式中，λ^T=（λ₁，λ₂，…，λ_l），▽h_k（X^*）T=（▽h₁（X^*），▽h₂（X^*），…，▽h_l（X^*））

为了说明拉格朗日乘子的物理意义，我们看函数f（X）=f（x₁，x₂）的一个二维问题，巨只有一个约束条件h（X）=h（x₁，x₂）=0时的简单情况。此时，式（2-25）的形式是

F（X，λ）=f（X）+λh（X）

由式（2-24）得

所以上式可以写成

式中的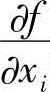是单位变量的目标值变化率，而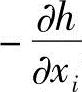则是单位变量的约束值变化率，可以称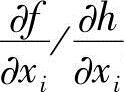为优化效率或敏度系数。而巨从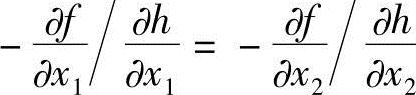可知，各变量的改变所导致的优化效率是相等的，巨等于一个常数λ。

对于机械优化设计问题，若目标函数f（X）是结构重量，约束条件是结构刚度或某点的变形，则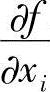可以理解为结构重量的收益，而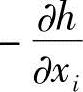可以理解为结构刚度的支出。则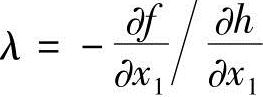就意味着单位结构的刚度支出所能获得的结构重量收益。这时的λ就反映结构刚度对其重量的优化率。

例2-2 用拉格朗日乘子法计算在约束条件h（X）=h（x₁，x₂）=2x₁+3x₂-6=0的情况下，f（X）=f（x₁，x₂）=4x²₁+5x²₂的极值点。

解：改造的目标函数是F（X，λ）=4x²₁+5x²₂+λ（2x₁+3x₂-6），则

由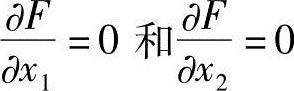

解得极值点坐标是

把它们代入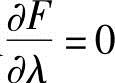（即约束条件2x₁+3x₂-6=0），求得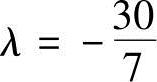

所以得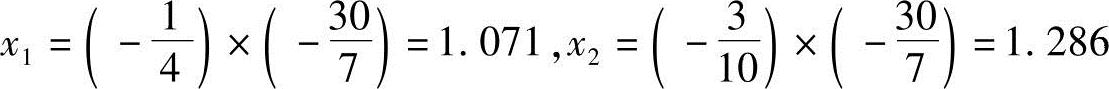

即极值点X^*=（1.071，1.286）^T