极值点存在的条件解析

1.一元函数（即单变量函数）的情况

（1）极值点存在的必要条件我们在高等数学中已经学过：如果函数f（x）的一阶导数f′（x）存在的话，则欲使x^*为极值点的必要条件为

f′（x^*）=0 （2-1）

仍以图2-5中所示一元函数为例，由图可见，在x^（1）与x^（2）处的斜率均等于零，即函数在该两点处的切线与x轴平行。但使f′（x^*）=0的点并不一定都是极值点，如图中的x^（3）点，虽然f′（x^（3））=0，但并非极值点而为一驻点。使函数f（x）的一阶导数f′（x^*）=0的点称为函数f（x）的驻点。极值点（对存在导数的函数）必为驻点，但驻点不一定是极值点。至于驻点是否为极值点可以通过二阶导数f″（x）来判断。

（2）极值点存在的充分条件若在驻点附近，有

f″（x）＜0 （2-2）

则该点为极大点；

若在驻点附近，有

f″（x）＞0 （2-3）

则该点为极小点。

在图2-5中的x^（3）附近，其右侧f″（x）＜0，但其左侧f″（x）＞0，因此它不是一个极值点。可见函数二阶导数的符号成为判断极值点的充分条件。

2.多元函数（即多变量函数）的情况

设f（x）为定义在X∈D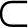Rⁿ中的n元函数。向量X的分量x₁，x₂，…，x_n就是函数的自变量。设X^（k）为定义域内的一个点，巨在该点有连续的n+1阶偏导数，则在该点附近可用泰勒级数展开，如取到二次项，有

如果用向量矩阵形式表示，则式（2-4）可写为

可简写为

式中，

Δf（X^（k））是函数f（X）在X^（k）点的一阶偏导数矩阵，称为函数在该点的梯度。梯度Δf（X^（k））是一个向量，其方向是函数f（X）在X^（k）点数值增长最快的方向，亦即负梯度-Δf（X^（k））。方向是函数f（X）在X^（k）点数值下降最快的方向，梯度的模

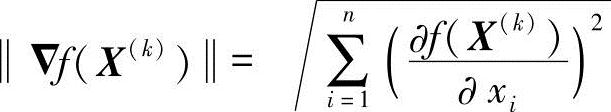
但需注意，函数f（X）在某点X^（k）的梯度向量Δf（X^（k））仅仅反映f（X）在X^（k）点附近极小邻域的性质，因而它是一种局部性质。函数在定义域内的各点都各自对应着一个确定的梯度。此外，函数f（X）在X^（k）点的梯度向量Δf（X^（k））正是函数等值线或等值超曲面在该点的法向量。图2-6表示二元函数f（X）在X^（1）、X^（2）点的梯度Δf（X^（1））、Δf（X^（2））和负梯度-Δf（X^（1））、-Δf（X^（2））。Δ²f（X^（k））是函数f（X）在X^（k）点的二阶偏导数组成的n×n阶对称矩阵，或称为f（X）的黑塞（Hessian）矩阵，记H（X^（k））。

式（2-4）～式（2-6）只取到泰勒级数二次项，称为函数的二次近似表达式。

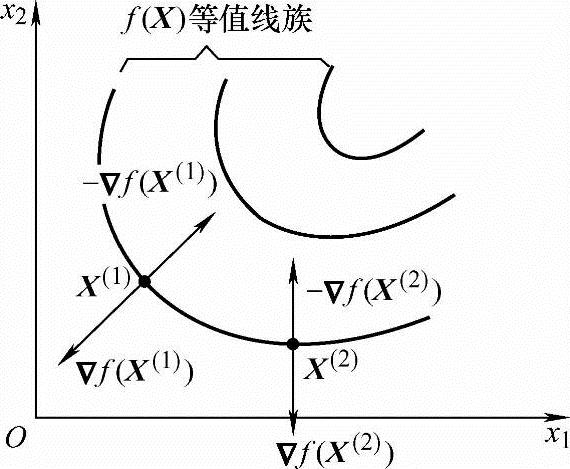
图2-6 二元函数的梯度和负梯度

（1）极值点存在的必要条件n元函数在定义域内极值点存在的必要条件为

即对每一个变量的一阶偏导数值必须为零，或者说梯度为零（n维零向量）。(www.xing528.com)

和一元函数对应，满足式（2-9）只是多元函数极值点存在的必要条件，而并非充分条件，满足Δf（X^*）=0的点X^*称为驻点，至于驻点是否为极值点，尚需通过二阶偏导数矩阵来判断。

（2）极值点存在的充分条件如何判断多元函数的一个驻点是否为极值点呢？

将多元函数f（X）在驻点X^*附近用泰勒公式的二次近似式来表示，则由式（2-6）得

因为X^*为驻点，Δf（X^*）=0，于是有

在X^*点附近的邻域内，若对一切的X恒有

f（X）-f（X^*）＞0

亦即

（X-X^*）^TH（X^*）（X-X^*）＞0 （2-10）

则X^*为极小点；否则，当恒有

（X-X^*）^TH（X^*）（X-X^*）＜0 （2-11）

时，则X^*为极大点。

根据矩阵理论知，由式（2-10）、式（2-11），得极小点的充分条件为

亦即驻点黑塞矩阵H（X^*）必须为正定。同理知极大点的充分条件为

亦即驻点黑塞矩阵H（X^*）必须为负定。而当

亦即驻点黑塞矩阵H（X^*）既非正定，又非负定，而是不定，f（X）在X^*处无极值。

至于对称矩阵正定、负定的检验，由线性代数可知，对称矩阵

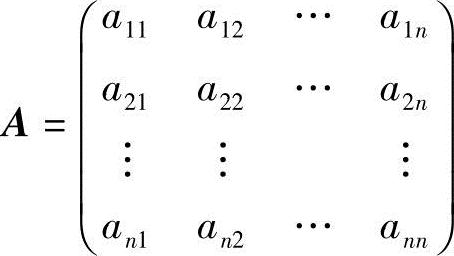
正定的条件是它的行列式|A|的顺序主子式全部大于零，即

负定的条件是它的行列式|A|中一串主子式为相间的一负一正，即

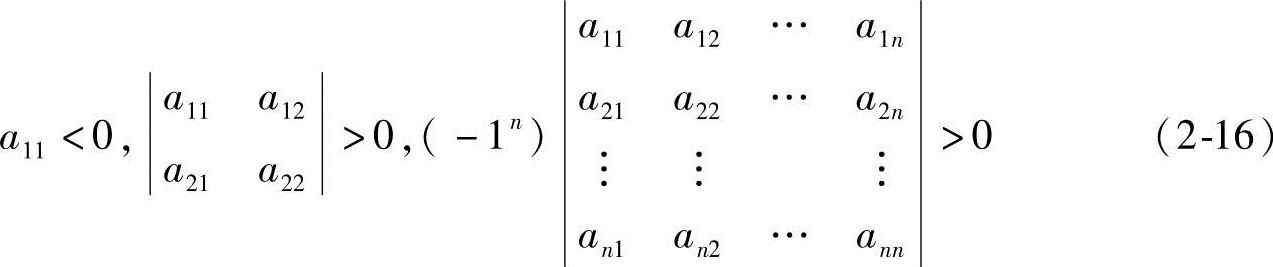
至此，读者完全不难自行归纳得出无约束目标函数极值点存在的充分必要条件和用数学分析作为工具对n维无约束优化问题寻求最优解。