谐波相位分析的评估方法优化

1.风电场电网谐波模型参数的评估方法

从图8.28的（c）、（d）图可以看出，风电机组谐波电压、电流分布情况符合图8.29所示的电流源模型，由此把机组看做250 Hz的电流源，可从单台机组690 V出口，计算出风电场电网的5次谐波阻抗。对于5次谐波有：｜U5｜＝｜I5｜×｜Z5｜，∠U5＝∠I5＋∠Z5。从以上数据可以计算得出风场电网参数：｜Z5｜≈0.06 Ω，∠Z5≈95°。同理可以计算出风电场电网对应其他各次谐波的模型参数。

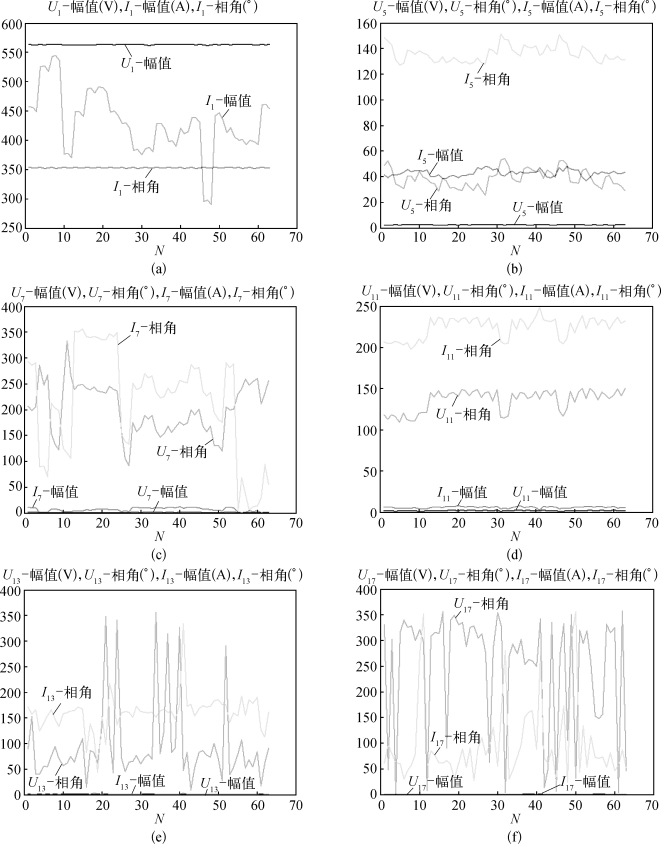
图8.27　基波及特征谐波电压、电流幅值相位分析

2.风机谐波相位的统计分析与评估方法

针对每个200 ms采样片段进行FFT计算，通过计算可以得出一系列复数结果X（k），每个X（k）中包含了相应分辨率下所有频率点的谐波的幅值和相位。从这些X（k）中找出与我们关注的、相对基波的整数n次谐波的频率点的k值及X（k），表示为hn，每200 ms数据计算出一个hn，第i次的结果为hni。则第i次求出n次谐波的相位角为：

图8.28　风机5次谐波电压、电流幅值及相位分布图

图8.29　风机－风场电网谐波模型

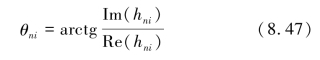
相关次谐波的相位可以用以上的方法直接求出，但往往其相位角有一定的离散性，如何对其相位角做一个统计，得出合理的平均相位角，有一定难度。

参考风资源评估中对于风能评估的风玫瑰图，提出了比较可行的一种与风速、风向评估类似的Bin方法，下面以5次谐波为例来验证本评估方法的直观性和实用性。由于对谐波相位角的测量和计算本身存在较大误差，实际应用中对谐波相位角的精度要求不高，以30°为一个Bin，做出图8.30所示的谐波分布曲线，可以直观判断5次谐波的分布情况。

很小幅值的谐波其相位角对整个风电场系统的影响很小，这个平均应该是一种加权平均，主要统计那些大幅值，长时间作用的谐波相位角。式（8.48）是对N次采集计算结果的加权平均统计公式。

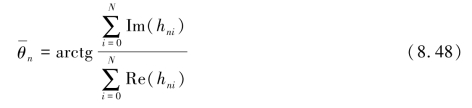
图8.30　风机谐波相位评估的Bin模型

除此之外，还可以统计该次谐波相位角的一致性。计算结果接近于1，说明一致性越高，风电场谐波的叠加效应越强。

(www.xing528.com)

实测数据的系统中，5、7、11次谐波相位角分布都比较集中，变化范围基本上集中在30°之内。其P（θn）值都接近于1。对于其他一些非特征谐波如图8.31所示，可能会有较大的离散性。

图8.31　风机谐波相位分布评估示意图

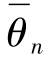图8.31可以很好的说明相位分布评估值P（θn）的作用，三个图中的横坐标为谐波相位角，纵坐标为对应谐波分量幅度的标幺值，分布的散点为测量计算出的该谐波的幅值和相位所对应的数据点，虚线为从这些测点中计算出的平均相位角。图中左边部分谐波的平均相位为0°，分布评估值P（θn）为0.9，中间部分的为80°，P（θn）为0.5，右边部分的为82°，P（θn）为0.2。这样我们就得到了与谐波幅度平均值计算相类似的相位角平均值和相位角一致性评价指标。

3.谐波的补偿与信号的准确快速还原

要精确定量分析风电场谐波的叠加情况，并对谐波电流的补偿，需要进行快速的谐波波形的还原，如图8.32所示。还原有两种基本方法，一种是FFT方法，对整个10个周波200 ms数据进行FFT计算，得出相应次数谐波的幅值和相位数据，再用这些数据还原出1个固定的谐波波形。此方法的优点是用于计算的点数较多，计算出的谐波幅值和相位数据较为精确。缺点是10个周波计算一个相位和幅值，每200 ms变化一次，实时性不好，与实际谐波波形有一定差距。而且计算量太大，同时计算出所有各次谐波的相位和幅值，实际需要还原应用的只是3、5、7、11等很少的几个数据，没有必要计算出所有的各次谐波。计算完成后可能就存在相位滞后，无法用于风电场谐波的叠加合成和实时的谐波补偿。

图8.32　风机各次谐波的补偿与信号检测还原

另一种方法是PLL锁相环方法，以宽度为20 ms的移动窗口来进行锁相环计算，还原出补偿所需要的几个主要频次的谐波。对于采用10 240 Hz频率采样得到的电压、电流信号，每周期约205个采样点，计算公式如下。

首先采用单相锁相环计算出指定谐波的幅值和相位：

代入计算还原出k次谐波电压、电流信号：

同理：

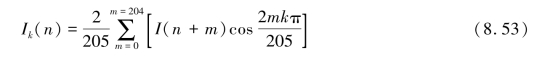
k＝1，3，5，7，11，13，17，19。n＝0，1，2，3，…，2 047。

图8.33为对5次谐波的电压电流信号的还原。采用本方法计算量很小，可以准确、快速的实现对所需要的各次谐波的检测还原，对特定频率谐波的补偿和综合分析提供了很大帮助。

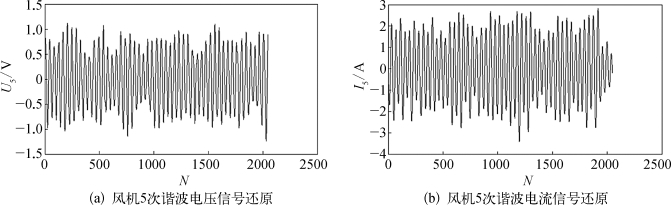
图8.33　风机谐波信号的还原