计算谐波相位方法简述

为了对比整个风电场各台机组的各次谐波相位，各次谐波都需要有一个统一的参考零点，以系统基波电压的零时刻为参考具有较好的一致性。相应的谐波相位的定义为：本相基波电压信号为0°时刻，谐波电压或电流的相位角。理论上式（8.38）和式（8.39）很容易得出各次的电压或电流谐波相位。但实际计算时，由于测量装置采样的零时刻不可能刚好与基波电压信号为0°时刻重合，而且三相基波电压之间存在相差，故需要在计算结果中减去本相基波电压相位角的n倍。

以5次谐波电压、电流相位角为例进行分析，如图8.25所示，若能够控制同步采样电路的启动时间，把数据采集的0时刻控制在基波电压的正向过零点，由此计算出的各次谐波电压相位αU5、电流相位αi5即为标准相位。否则对5次谐波，需要减去基波相位角的5倍。实际操作中因为三相基波电压的过零点互差120°，不可能在同一时刻启动采样，还是需要进行相应的相位角修正。

图8.25　谐波电压、电流幅值相位分析示意图

对如图8.26所示的一组实测数据进行计算，通过简单算例说明具体计算过程，并分析对提高整个风电场电能质量的意义。基本采样数据要求10 kHz至20 kHz采样频率，对整个10个周波200 ms数据进行FFT计算，得出相应次数谐波的幅值和相位数据。以下分析数据采样与同一台2 MW风机5 m/s风速段，原始采样数据为21个200 ms（每段数据2 048个三相电压、三相电流和中线电流），每分钟1个200 ms采样数据段，共采样20 min。采用10.24 kHz采样频率，相比整10 k或20 kHz采样频率，其优点是整10、20周期数据量都是2的N次方，采样FFT计算避免了截断误差或频谱泄露，其结果中的特征谐波点都对于整数点，避免了频率误差。由此计算一段实时测量的风机数据，并列出幅值较高的主要频次谐波，比较其相位评估方法。

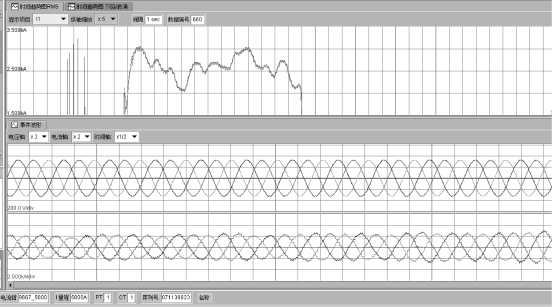
图8.26　2 MW风电机组电压、电流实时采样数据

计算方法流程如下。(www.xing528.com)

首先，对每段的2 048个采样点用FFT算法得到：

x（n）分别为对某一相的电压、电流采样数值u（n）或i（n），相应的从其复数结果X（k）中可以计算出电压、电流的幅值和相角。ABS为复数取模，Angle为复数取幅角函数，频率分辨率为5 Hz，实际对应的信号频率为k的5倍。根据式（8.41）～式（8.43）分别得到电压直流分量Udc、基波电压幅值U1和基波电压相位。

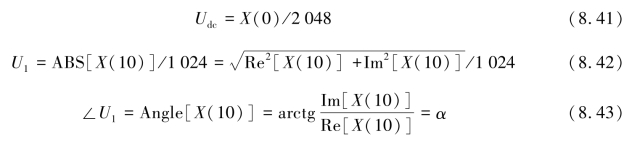
其中基波电压相位的准确性非常重要，因为各风机采样没有一个统一的时标，要进行相位对比，必须有一个共同的时间起点。整个风电场各台风机最终汇入一个接入点，并且同一风电场同类型风机的接入变压器基本一致，虽然线路长度有差别，但其总阻抗彼此间差距不大，所以其基波相位基本一致。主要特征谐波相位的计算对比都要以基波相位为准，基波相位测量的微小偏差都会对谐波相位计算准确性参数很大影响。

同样可以根据式（8.44）～式（8.46）得出各分数次谐波和间谐波的幅值和相位角，在当前测量方式下频率分辨率为5 Hz，由此可以计算出从直流到5 kHz每隔5 Hz的各频率点的间谐波幅值和相位。

图8.27（a）中把基波电压相角调整到0°，相应的电流相角即为功率因数角。从（b）、（c）、（d）中可以看出，在整个测量时段内，5、7、11次谐波的幅值和相位角都相对较为稳定。（e）、（f）对应的是13次和17次谐波，幅值很大小相位角变化较大。主要原因是13次以上谐波幅值较小，频率高、周期短，对基波相位测量的微小误差都会造成很大的相位角波动。