基于证据理论的振荡源在线定位方案

1.证据理论

不同振荡源定位策略的适用性不同，得出的结果对于不同的振荡类型、不同的振荡复杂性的参考价值也不同。因此，当系统中出现振荡时，无法采用单一的方法来确定振荡源，而不同策略的振荡源判定结果也可能会互相冲突。因此可以将这种确定性的定位转化为概率问题，对于不同的定位策略可以给出相应的定位结果和结果的可信度概率。这样可以解决不同结果的矛盾冲突，也可以综合多种适合不同场景的方案给出振荡定位结果。

这里采用证据理论对不同的振荡定位信息进行融合。

在证据理论中，会有一个基本的假设空间，记为Θ。针对大部分的振荡问题，可以将定位问题转化为对每个输出节点是否是振荡源的分析。Θ就包含了两个元素，即

Yes表示该节点是振荡源，No表示该节点不是振荡源。证据理论中的几个概念：

（1）质量函数

在假设空间中，质量函数是2Θ→［0，1］的函数，记为m，定位问题中m即是否是振荡源的概率函数。m满足：

即是振荡源和不是振荡源的概率之和为1。

（2）信任区间

DS证据理论中信任函数可以用来给出概率的下限，定义为

DS证据理论中似然函数可以用来给出概率的上限，定义为

综合信任函数和似然函数就可以给出输出结果的信任区间为［Bel（A），Pl（A）］。

（3）合成规则

DS证据理论的核心是合成规则，∀A⊆Θ，Θ上的n个质量函数m1，m2，...，mn的合成规则为

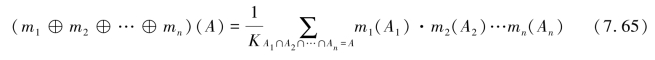
其中，K为归一化常数：

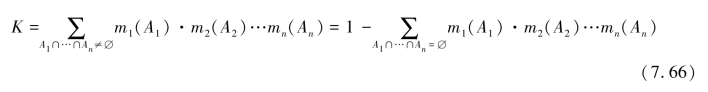
2.三种用于振荡源定位的基本方法

（1）振荡能量流法

按照振荡能量流理论，定义一个节点或一个系统割集的振荡能量为

展开可得：

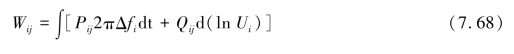
标幺制系统中，可知ln Ui很小，经计算发现第二部分积分可以忽略不计。故振荡能量可以由近似表示。

设流出节点或割集的电流为正，当一个节点的振荡能量为正，振荡能量曲线有正斜率时，说明该节点一直在向外输出能量，是振荡源；当一个节点的振荡能量为负时，振荡能量有负斜率，说明该节点一直在接收振荡能量，不是振荡源。根据这个原理分别对强迫振荡案和负阻尼振荡案例进行分析。

（2）振荡相位差法

在电网中，要想输出功率，两个节点的电压之间必须要有角度差，即功角。当其中一个节点成为扰动源时，沿着振荡扩散的方向，节点电压的振荡相位也依次后延。因此振荡源电压角度振荡相位应超前于与振荡源相连的节点电压的角度振荡相位。

以3ND为例，该振荡是振荡源为节点11的负阻尼振荡，故障源为节点30，另外，节点6具有弱阻尼特点。关注这3个节点的电气量和机械量。对所研究的节点和相邻节点的电压角度曲线进行FFT分析，对相应幅值最大的分量的相位进行对比分析得到表7.22。

表7.22　案例3ND部分节点电气量和机械量相位差分析

可见节点11满足判定条件。但值得注意的是，算例中给出的振荡模式是单一的，FFT分解可以很好的获得主要振荡模态，进而可以做相应的分析。而实际运行中，振荡发生时，PMU测量的数据干扰大，振荡相位往往是在一直变化的，无法通过一个瞬间的振荡相位差来判断振荡源属性。故用式（7.69）来定义相位差指标：

φ1和φ2分别为振荡源节点和相邻节点的电压角度振荡相位。要求取该指标，需要引入HHT来求瞬时的振荡相位。

HHT算法由经验模态分解（EMD）和希尔伯特变换（HT）两部分组成。EMD将信号分解为固有模态函数（IMF）。IMF是满足极值点与过零点相差不能够多于一个且局部极大值极小值平均值为0的信号。利用HT可以获得IMF分量在任意时刻的相位、频率和幅值。采用插值法对极值点进行拟合。

给出振荡相位差法的流程如图7.37。

图7.37　振荡相位差法判定流程图

锁定节点电压角度和相邻节点电压角度数据，对二者进行EMD分解，获得IMF分量；接着对IMF分量进行HT，提取瞬时相位，获得瞬时相位差，最后积分得到相位差指标，如果指标为正，判定该节点为振荡源；为负则判定为非振荡源。

（3）强迫振荡相位差判定法

根据发电机转子的标幺制运动方程(www.xing528.com)

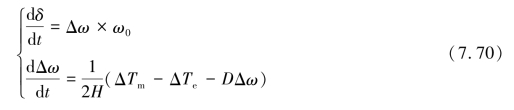
其中，δ为转子角；ω为角速度；H为惯性常数；ΔTm为机械转矩；ΔTe为电气转矩；D为阻尼系数。

假设功率的标幺值与转矩一致，这一简化影响可以忽略。则

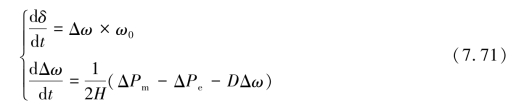
其中，ΔPm为机械输入功率；ΔPe为电气输出功率。

已知从而可以推导出已知的计算公式。

ΔPm、ΔPe之间的关系：

其中，Ω为功率波动的角频率，K（s）为原动机及调速器的传递函数。可见如果ΔPm与ΔPe的波动相位差大于0，则该机组为振荡源。判定流程如图7.38所示。

3.振荡源在线定位融合模型

给出振荡源定位的建模流程如图7.39所示。首先采用三种适用性不同的振荡源定位方法对节点进行振荡源定位分析，得到证据理论的输入规则集合，再利用DS证据理论对三方信息进行融合，得到合成规则及合成规则的信任函数和似然函数值。

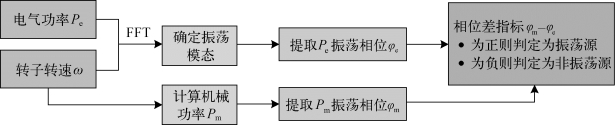
图7.38　强迫功率振荡相位差判定法流程图

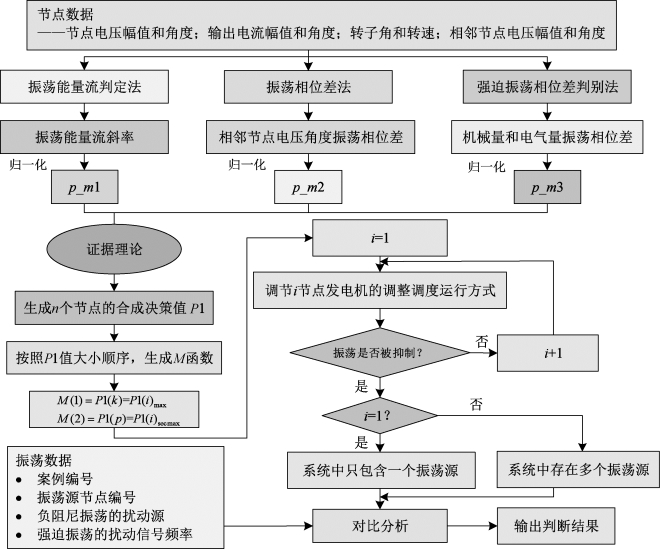
图7.39　振荡源定位算法建模

4.质量函数的构建

上面给出了三种判定振荡源的方案，对于振荡能量流法和振荡相位差法，负阻尼振荡和强迫振荡均适用，当振荡能量流法的斜率最大，或者振荡相位法的相位差最大时，相应节点为振荡源的概率设置为1，接着选择变化先快后慢的函数生成初始化概率pp，pp满足：

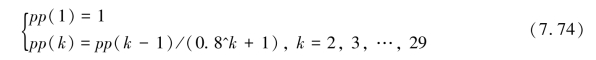
给定一个节点i，在一个案例中，将所有29个节点的振荡能量流曲线斜率进行从大到小的排序，假定节点i的振荡能量流曲线斜率排在第j_m1个，则定义振荡能量流法的质量函数p_m1为

将所有29个节点的电压角度振荡相位差进行从大到小的排序，假定节点i的振荡能量流曲线斜率排在第j_m2个，则定义振荡相位差法的质量函数p_m2为

在强迫振荡相位差判定法中，将所有29个节点的机械和电气振荡相位差进行从大到小的排序，假定节点i的振荡能量流曲线斜率排在第j_m3个，则定义强迫振荡相位差法的质量函数p_m3为

5.证据理论模型

利用上述结论，可以合成所示的证据理论原始表格。对于某一节点，证据理论的模型构建如表7.23：

表7.23　证据理论模型

其中：

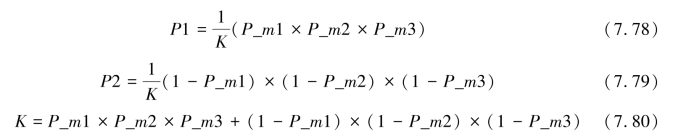
6.算例

将方法应用于一个多源复杂仿真系统，该电网具有电网位置偏远、用电负荷较轻、网架结构相对薄弱的特点。该系统中，风电和光伏通过辐射网络接入交流系统，在新能源发电系统和直流输电系统附近存在汽轮发电机组，形成风光火打捆经直流外送系统。在PSCAD/EMTDC中仿真的时域模型，观察系统是否会出现次同步振荡现象。设置一种典型仿真条件，风机出力水平为4%左右，光伏出力水平为0.3左右，在0.7 s时刻提高线路连接电抗（模拟电网强度变弱）。

对仿真案例采用振荡能量法进行分析。计算得到11个发电机节点的振荡能量以及各个节点电气功率、机械功率、电压的幅值和相角，所有节点的振荡能量图、振荡相位差指标以及强迫功率振荡相位差指标如图7.40。

振荡能量流法：从图7.40（a）分析可知，振荡源节点5，6和7的振荡能量的输出随时间持续增加，且节点7为斜率最大的节点，由此，可以得出该方法可以较有效的定位出振荡的节点。其中节点7由于斜率最大，很有可能为振荡发生的原始节点。

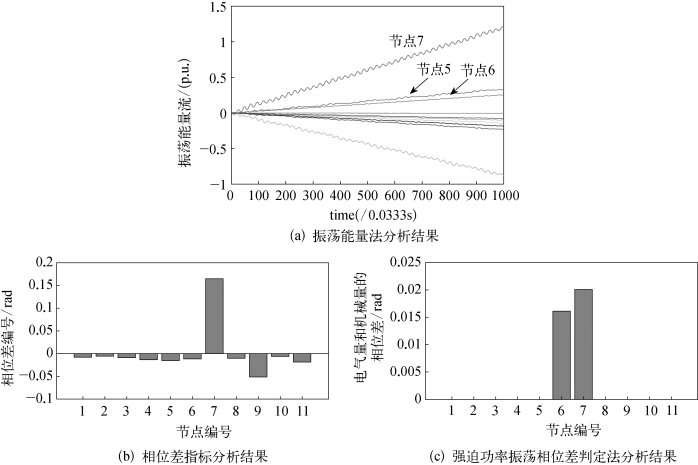
图7.40　3种传统振荡定位方法的结果分析

振荡相位差法：由图7.40（b）所示，仅有节点7被正确定位出，节点5和节点6都被漏判。

强迫功率振荡相位差法：由图7.40（c）所示，采用强迫功率振荡相位差判定法，节点6和7被有效定位，但是节点5没有被判定出，因此有一定程度上的漏判，从而对振荡抑制策略产生影响。

采用三种方案计算质量函数，结果如图7.41（a）：计算合成规则，得到结果图7.41（b）：

从图7.41（b）的合成规则得到结果可以看出，经过证据理论的优化后获得的判定结果，节点7是概率函数最高的节点，为2.804。按照合成规则得到的大小顺序依次消除振荡，节点7被优先考虑；同理，节点70和节点30的合成规则的值也为正，也可判定为潜在的振荡源。与振荡源信息对比发现，判定正确。

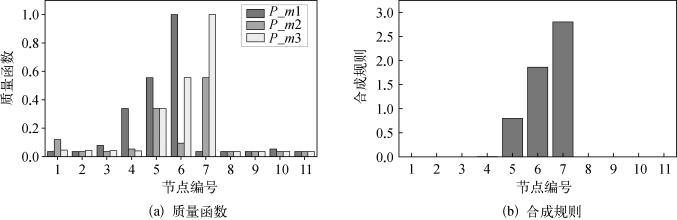
图7.41　证据理论模型分析结果