基于随机矩阵原理的数据源构建方法

1.随机矩阵理论

随机矩阵理论是对复杂网络进行统计分析的重要数学工具之一。随机矩阵理论通过对复杂系统的能谱和本征态进行统计分析，得到复杂系统的本征，并能从随机数据中分析数据关联性，以表征数据的波动特性，还能将数据特征映射到物理系统中。随机矩阵理论能够分析高维度大样本数据，并对传统统计分析呈现病态的高维度小样本有一定的适用性。

在实际系统中，变量受到外部环境影响，数值呈现一定的随机性。将实际系统中变量数据按照一定规则排列，可得到元素具有一定随机性的矩阵，可将这种矩阵认为是随机矩阵。随机矩阵理论在金融、交通、量子物理学和无线通信等领域已得到了广泛应用。这些特征为随机矩阵理论在电力系统的应用提供了理论基础和实践经验。本文以随机矩阵理论为基础，结合时间序列特征，分析时空大数据，并从中挖掘有效信息，用于辨识电网运行状态。

（1）Marchenko-Pastur定理（M-P定理）

M-P定理可用于描述大维协方差矩阵的特征值分布，具有较强的适用性。假设X＝｛xij｝为N×T阶非Hermitian随机矩阵中元素为独立同分布，且满足μ＝0，方差μ＜∞。当N，T→∞且c＝N／T∈［0，1］时X的样本协方差矩阵SN的经验谱分布非随机的收敛于密度函数如式：

其中为样本协方差矩阵SN的特征值；。

（2）单环定理

假设X＝｛xij｝为N×T阶非Hermitian随机矩阵中元素独立同分布且满足E（xij）＝0，E（｜xij｜2）＝1。考虑L个非Hermitian矩阵的情况，令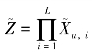，其中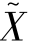为非Hermitian矩阵X∈N×T的奇异值等价矩阵。当N，T→∞且c＝N／T∈（0，1］时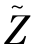，的经验谱分布几乎一定分布于单环定律，概率密度函数如下：

根据单环定理，高维非Hermitian矩阵特征值将分布于外环半径1和内环半径（1－c）2／L之间。

2.基于增广矩阵法的数据源建立

假设在电网中，可量测的电网状态变量有ng个，待研究的影响因素有nf个。经过T次采样，ng个电网状态变量的量测数据可以构成一个矩阵称为状态数据矩阵；nf个影响因素的量测数据可以构成一个矩阵，称为因素数据矩阵。

在大多数情况下，电网状态变量的个数ng大于（甚至远大于）待研究的影响因素的个数nf。因此，首先需要对因素矩阵进行扩展。因素矩阵的扩展分为2个步骤。

第一步，将因素数据矩阵复制k次，如式（7.41）所示。

其中，k＝［ng／nf］，［·］是不超过“·”的最大整数。

第二步，在Dc中引入随机噪声，以降低重复数据的相关性，如式（7.42）所示。

其中，Ef为因素扩展矩阵；为噪声矩阵，每一个元素都是服从标准正态分布的随机变量；m为噪声的幅值。噪声幅值的大小会影响相关性分析的结果，如果噪声太小，则Dc中重复数据的相关性将会造成干扰；如果噪声太大，将会降低De中数据的真实性和准确性。为此，我们定义因素扩展矩阵Ef的信噪比（signal-to-noise ratio，SNR）为

其中，Tr（·）为矩阵的迹。为了保证分析结果的一致性，在分析不同影响因素时需要采用相同的信噪比。

利用状态数据矩阵和因素扩展矩阵，按式构造增广矩阵，作为相关性分析的数据源。其中状态数据矩阵为数据源的基本部分，因素扩展矩阵为数据源的增广部分。

此外，为了排除状态数据矩阵中数据相关性对结果的干扰，可以利用状态数据矩阵和噪声矩阵构造一个参照增广矩阵，如式（7.45）所示。

3.线性特征值统计量与平均谱半径

矩阵的线性特征值统计量（linear eigenvalue statistic，LES）是通过连续检验函数（continuous test function）φ：来定义：

式中，λi（i＝1，2，…，n）为矩阵X特征值，φ（g）是一个测试函数，选择不同的测试函数，线性特征值统计量的形式也不同。(www.xing528.com)

平均谱半径（mean spectral radius，MSR）是一类特殊的LES，它是矩阵特征值在复平面上到原点的距离。系统状态发生变化时，随机矩阵的迹会随之发生改变，MSR能够反映这种变化的动态过程，可以作为评价指标。MSR的定义如下：

式中，rMSR表示随机矩阵的平均谱半径，λi（i＝1，2，…，n）为矩阵的n个特征值。

LSE描述了随机矩阵的迹，大数定律（law of large numbers）和中心极限定理（central limit theorem，CLT）表明，对于一个随机矩阵而言，矩阵的迹能够反映矩阵元素的统计特性，而矩阵的单个特征值由于具有随机性而无法反映这种特性。因此，作为线性特征值统计量的一种，平均谱半径能够反映随机矩阵的统计特性。

4.相关性分析方法的步骤

本书采用平均谱半径作为相关性分析的指标，将平均谱半径与单环定理的理论预测进行比较，可以反映数据之间的相关性。在每个采样时刻，比较增广矩阵和参照增广矩阵的平均谱半径，揭示影响因素与电网运行状态的相关性。定义平均谱半径差为

其中，κMSR，AN、κMSR，A分别为参照增广矩阵和增广矩阵的平均谱半径。dMSR－t曲线能够反映影响因素对电网运行状态的作用规律。定义平均谱半径积分为

sMSR能够定性表征影响因素在T次采样内与电网运行状态的相关程度。

基于随机矩阵理论和增广矩阵法，这里提出一种针对电网运行状态的相关性分析方法，其流程如图7.31所示。

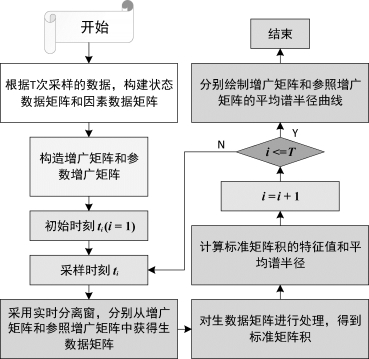
图7.31　相关性分析方法流程

电网的运行状态是各种影响因素共同作用的结果。这些影响因素以直接或间接的方式影响电网的运行状态，并且彼此之间存在耦合关系。提出的相关性分析方法是基于统计学理论的大数据分析方法，能够分析复杂系统中海量数据的相关性。在分析相关性的过程中，不涉及各种影响因素与电网运行之间的作用机理，也不需要对每种影响因素进行解耦；同时不受限于电网规模和结构，也不需要预知电网具体参数。因此，与模型法相比，提出的方法一方面不涉及对问题的假设和简化，提高了分析的准确性；另一方面能够用于分析各类因素对电网的直接或间接影响，提高了方法的通用性，从而更好地应对电网规模庞大、运行机理复杂、随机程度高的发展趋势。此外，与其他数据挖掘技术相比，提出的方法采用了实时分离窗技术，能够实时分析数据相关性。

5.算例分析

将各节点的有功负荷视为电网运行状态的影响因素，分析影响因素与电网运行状态的相关性，取不同类型和数量的电网状态变量构造状态数据矩阵，与单一影响因素进行相关性。

电网状态变量类型和数量的选择：

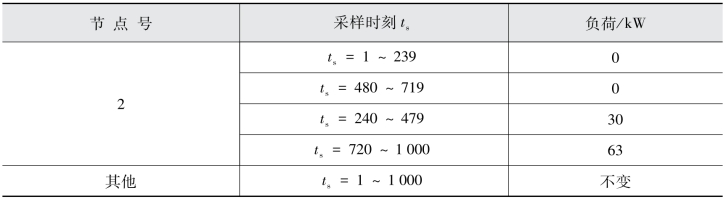
取不同类型或数量的电网状态数据构造状态数据矩阵，分别与全网各节点的有功负荷进行相关性分析（nf＝1），算例中节点2有功负荷的变化情况如表7.18所示，其中ts表示采样时刻的序号。设Tw＝75，ρ＝500，T＝200。

表7.18　节点2有功功率的变化情况

取全网节点的电压幅值数据构造状态数据矩阵（ng＝33，Nw＝66）。对整个节点网络全采样时刻进行分析，通过计算高维统计指标MSR来分析其状态。当受振荡影响时，状态矩阵的特征根将会发生坍塌，可知MSR在此时也会发生突变。

结合这两点，这里提出电网扰动定位的方法。以节点拓扑图为依据，将整个节点网络按照拓扑关系进行分割，如图7.32所示。

图7.32　全网节点有功负荷的平均谱半径曲线

在采样时刻ts＝240，节点2的负荷由0上升到30 MW。此时状态数据不再只有高斯白噪声，振荡事件影响了状态数据间的相关性，从而使得状态数据不再符合单环定理。

在图7.32中，由于T＝200，MSR的计算从ts＝200开始。ts＝239时，MSR在0.9附近，而ts＝240时候则突变到0.6附近，说明在ts＝200时，节点网络受振荡事件影响。

比较增广矩阵和参照增广矩阵的平均谱半径曲线，可以得到以下信息：

（1）ts＝439时，采样时刻ts＝240～439中的状态数据都是在新的状态下达到平衡，所以此时MSR恢复到初始水平。需要注意的是，MSR恢复了稳定，并不说明系统在一个采样周期内波动就结束了。本书的方法是采用数据驱动，不涉及具体的机理过程，所以算例并不涉及电网的暂态过程。在不同的状态下达到平衡后MSR都会恢复到0.9附近，而与不同的状态无关，这是因为E（φMSR）只与维容比有关。分析ts＝240和ts＝480以及ts＝720时MSR的突变可知，振荡功率变化越大则MSR突变程度越大。

（2）κMSR，A和基本相同，dMSR取值在0附近。这说明影响因素数据和电网状态数据之间不具有相关性，即节点2的负荷与电网运行状态无关。

（3）影响因素数据和电网状态数据之间存在相关性，即节点2的负荷影响了电网运行状态。