基于动态数据的影响因素特征提取技术优化

根据当前工程的实际观测，风电机组的机网相互作用往往发生在低风速下，同时，接入PCC点的电压变化也会产生同样的作用。为了探究风速和电压的这两种因素的共同作用对风电机组振荡模态的影响，本章采用K-Means算法对测量数据按风速和电压指标进行聚类。聚类后，同一聚簇的影响因素组合具有相同的特征。

根据K-Means算法中k值的选取方法，首先选取较少的样本，以获得最佳分类聚簇数。拥有最佳聚簇数的聚簇中心，可以在进一步分析中设置为聚簇中心初值，以保证聚类中心的一致性。

为了探究风速和电压对风机输出功率的影响，选定风速和电压波动为研究对象。其中，电压波动指每个Prony分析的数据段中电压三相电压有效值的极差的平均值，如式所示。

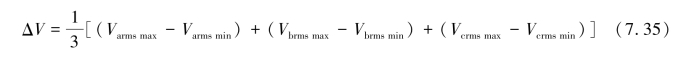
统计发现，存在三相电压的波动不平衡点，部分不平衡点如表7.12所示。总电压波动指标使得这些不平衡点回归“正常”，故将ΔVa、ΔVb、ΔVc、ΔV均纳入聚类的特征指标中。

表7.12　三相电压波动量的不平衡点

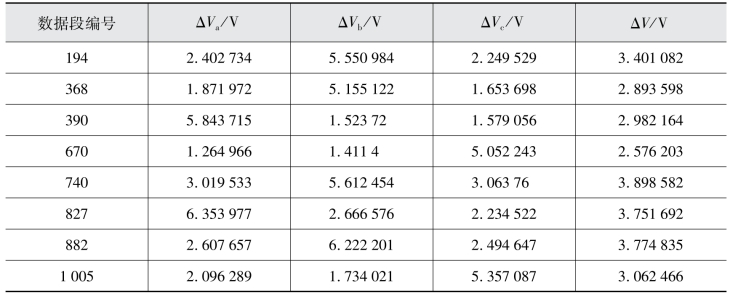
同时，与功率数据的预处理一样，将每40个点的风速值取平均作为一个采样点的风速值，作为每个数据段的风速因素值。这样，每个Prony分析的数据段对应一个风速值WS和电压波动值ΔVa、ΔVb、ΔVc、ΔV。为了研究5个变量的共同作用，按这5个变量对数据段进行聚类。

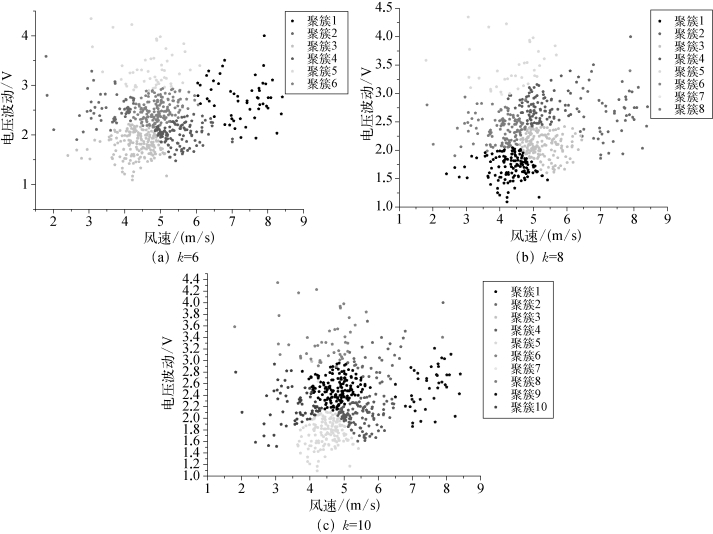
为了确定最佳聚簇范围，首先取600个数据段，取k分别为6、8、10进行聚类分析，将聚类结果以风速为横坐标，三相电压波动为纵坐标，得到如图7.27所示的聚类结果，不同颜色表示不同的聚簇。

(www.xing528.com)

图7.27　不同聚簇数下的K-Means聚类结果（后附彩图）

k＝6时，这600个点被分为了6类，如图7.27（a）所示。从风速和ΔV的二维平面上看，聚簇与聚簇之间有明显的区分。其中聚簇1为图中黑色数据点，电压波动在2 V到3.5 V之间，风速值在6 m/s以上；聚簇2为图中红色数据点，电压波动也在2 V到3.5 V之间，风速值在4 m/s以下；聚簇3为图中绿色数据点，电压波动在2 V以下，风速值在5 m/s以下；聚簇4为图中深蓝色数据点，电压波动在1.5 V到2.5 V之间，风速值在5 m/s到7 m/s之间；聚簇5为图中淡蓝色数据点，电压波动在3 V以上，风速值在3 m/s到6 m/s之间；聚簇6为图中枚红色数据点，电压波动在2 V到3 V之间，风速值在4 m/s到6 m/s之间。

k＝8时，与k＝6时相比，基本聚类结果分布不变，但是多了2个聚簇，这两个聚簇中均只有一个点，如图7.27（b）黄色聚簇和枚红色聚簇，这两个聚簇反映了三相电压的不平衡性，应当被保留，故可见取k＝8要比k＝6更适合，但考虑到还有三个相电压的波动量不能在图中体现出来，故还有比k＝8更合适的聚类数；进一步看聚簇10，可见聚簇10中多了3个元素含量很少的聚簇，在原有的基础上进一步将聚簇6中的6个聚簇细分为了7个。表7.13给出了聚簇的分类情况。

表7.13　　k＝10分类结果

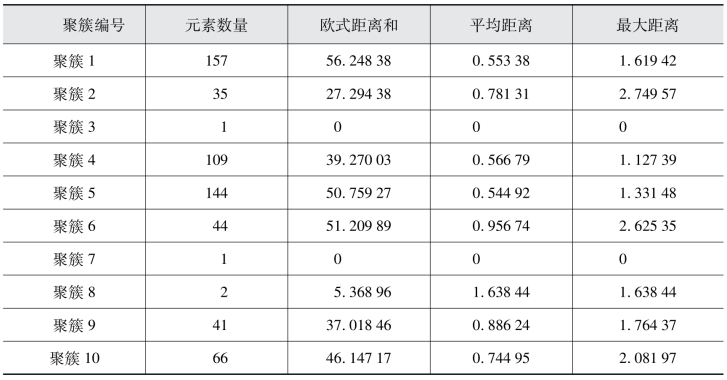
可见聚簇3、聚簇7、聚簇8为数量较少的聚簇。进一步看聚簇中心如表7.14所示。

表7.14　k＝10聚簇中心

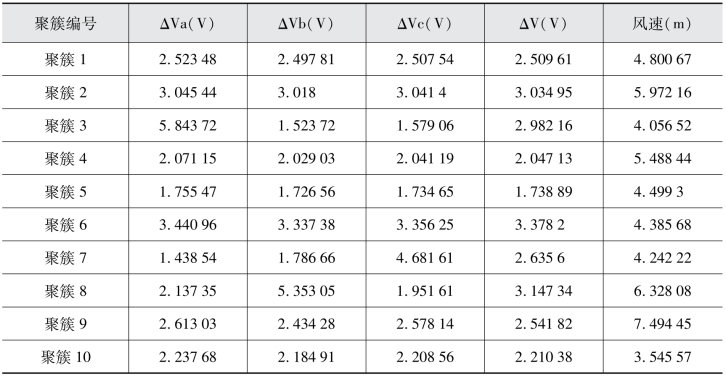
可见聚簇3存在a相电压波动与bc相的不一致，聚簇8存在b相电压波动与ac相的不一致，聚簇7存在c相电压波动与ab相的不一致。聚簇数为10可以很好地将这几个非正常的运行状态分类出来。故相比于k＝6和k＝8更具有优越性。

最后定义特征标记方案以便于后面的关联分析，若k＝10时，当某一数据段被分在簇1中，则该数据段的标记为［聚簇1，聚簇2，聚簇3，聚簇4，聚簇5，聚簇6，聚簇7，聚簇8，聚簇9，聚簇10］＝［1，0，0，0，0，0，0，0，0，0］。