基于风电大数据HHT分析的振荡识别优化方案

1.HHT分析方法

（1）经验模式分解（EMD）原理

对于一个平稳的信号x（t），经由傅里叶变换后，其可表示为

对于平稳信号，式（7.17）的变换结果是行之有效的。然而，在实际的应用中，常常要应对的处理信号则基本为非平稳的信号。此时，式（7.17）的变换结果则是不能够进行有效表示原始信号的。

经验模态分解的基本思路是将一个频率不规则、波动的非平稳信号分解为多个单一频率分量与残余分量部分，如式（7.18）所示。IMF分量即为原始信号的不同时间尺度的局部特征信号，而残余分量则蕴含着原始输入信号的发展走向的信息。

也可表示为

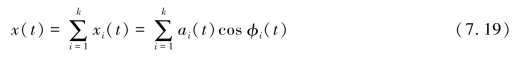
在式中，xi（t）能同时表征信号的幅值和频率跟随时间的变化情况。

EMD方法是一种自适应的数据处理与挖掘的算法。在EMD分解过程中，第1步是寻找输入信号的极值点；第2步是绘制包络线，并求解包络线的平均值；第3步是将输入信号与包络线平均值作差，即可得到可能的IMF分量之一；第4步是判断IMF是否满足终止条件，满足条件终止；否则返回第一步。

在EMD分解过程中，EMD分解是先将高频段的分量IMF1先提取出来，再依次从高频段到低频段将各个IMF分量分离出来。同时，对于原来复杂的非平稳的功率信号，被分解成了多个IMF分量，这样对功率信号的研究转换成了对EMD分解后的较为简单的IMF分量的研究。在风电场采集的数据中应用EMD算法，一方面可以有效滤除原始数据中存在的畸形波，另一方面可以降低相近波形间的振幅差距。另外，分解出来的IMF分量可以便于后面的分析工作。

（2）HHT变换

一般来说，经过EMD处理的信号是唯一的，同时常被用来分析信号自身包含的局部动态特性。对于一个连续的信号x（t），其Hilbert变换y（t）的计算方法为

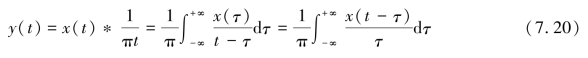
式中，“*”表示x（t）与1／（πt）的卷积。一般原始信号x（t）经过HHT变换，正频率的分量相当于进行了顺时针旋转90°的操作，负频率的分量则逆时针旋转90°。x（t）的解析信号z（t）可表示为

对于被分析信号的瞬时相位φ（t）、瞬时频率f（t）、瞬时幅值A（t）、Hilbert幅值谱H（ω，t）、Hilbert边际谱h（ω）的计算方法参照等式所示。

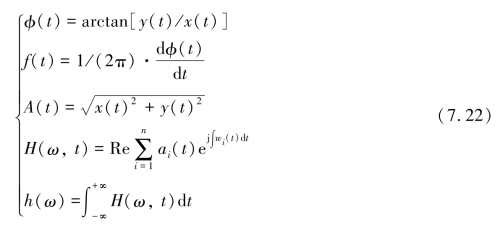
常见的HHT信号分析的整个流程囊括EMD和Hilbert变换，其完整的程序流程参照图7.20所示。此外，针对研究问题本身的差异以及需求，可相应计算分解信号的瞬时频率、相位、幅值和幅值谱、边际谱等信息，从而实现对原始信号的分析。在本部分的研究中，HHT分析方法可以从非平稳的风电场原始数据中挖掘出有关振荡现象的信息，从而支持风电场机网相互作用的研究。

图7.20　基于希尔伯特－黄变换的信号分析方法流程图

2.基于HHT的振荡分析方法

（1）IMF分量的预处理

在利用HHT变换对原始的输入信号进行分析的过程中，一方面出于剔除噪声信号干扰的目的，另一方面为了消除无关分量的影响，可以通过IMF分量的能量占比和功率波动对分解出的IMF分量进行遴选：能量占比越大、功率波动越剧烈的信号在原始信号中起的作用就越大，另外输出功率的波动情况也与风电机组并网点的运行状态相关。

以IMF分量振幅为衡量能量多少的特征，故第i个IMF分量的能量Ei的计算方式为

式中，N表示用于分析的离散信号的数据点数，Aij（t）表示第i个IMF分量在第j点的振幅值。

第i个IMF分量的能量占比E′i的计算式为

式中，M表示分解出的IMF分量的个数。

IMF分量的功率波动P′i的计算式为

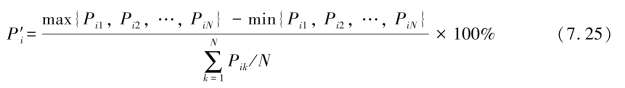
式中，Pik表示第i个IMF分量在第k点的有功功率值。(www.xing528.com)

（2）适用于IMF分量的特征参数提取

对于第i个IMF分量，描述其变化趋势的方程可表示为

式中，Ai0表示第i个IMF分量信号的初始振幅，λi表示衰减因子，wi表示频率值，θi0表示初始相角。

第i个IMF分量信号的瞬时幅值为

对式两侧取对数，可得到

相应地，瞬时相位φ（t）的计算式为

接下来，可以通过数据拟合的方式求得IMF分量的特征参数值，如振幅（Ai0）、衰减因数（λi）、角频率（wi）、初始相角（θi0）。另外，阻尼比的计算式为

基于HHT变换的信号分析流程参见图7.21所示，其主要分为五个步骤，即EMD分解、能量占比与功率波动计算、筛选、求解、曲线拟合。

图7.21　基于HHT变换的信号分析流程

3.算例分析

（1）EMD分解及IMF分量处理

本部分用于分析的数据时间长度10 s，且为连续采集的结果，数据包含40 000个点。双馈风电机组的机端输出有功功率的曲线如图7.22所示。从图中可以看出，实际测算得到的瞬时功率随时间的波动较大，是一个典型的非线性、非平稳信号，可以且比较适合用HHT分析的方法进行分析。

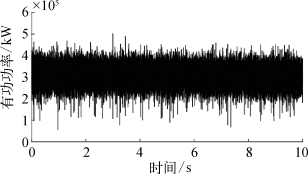
图7.22　双馈风电机组输出有功功率

表7.7　每个IMF分量的能量占比情况

对输出有功功率的信号进行EMD分解，其结果如图7.23所示，其包含13个IMF分量和一个残余分量。从IMF1～IMF13的图像可以看出，EMD分解后得到了不同频率段的功率信号。

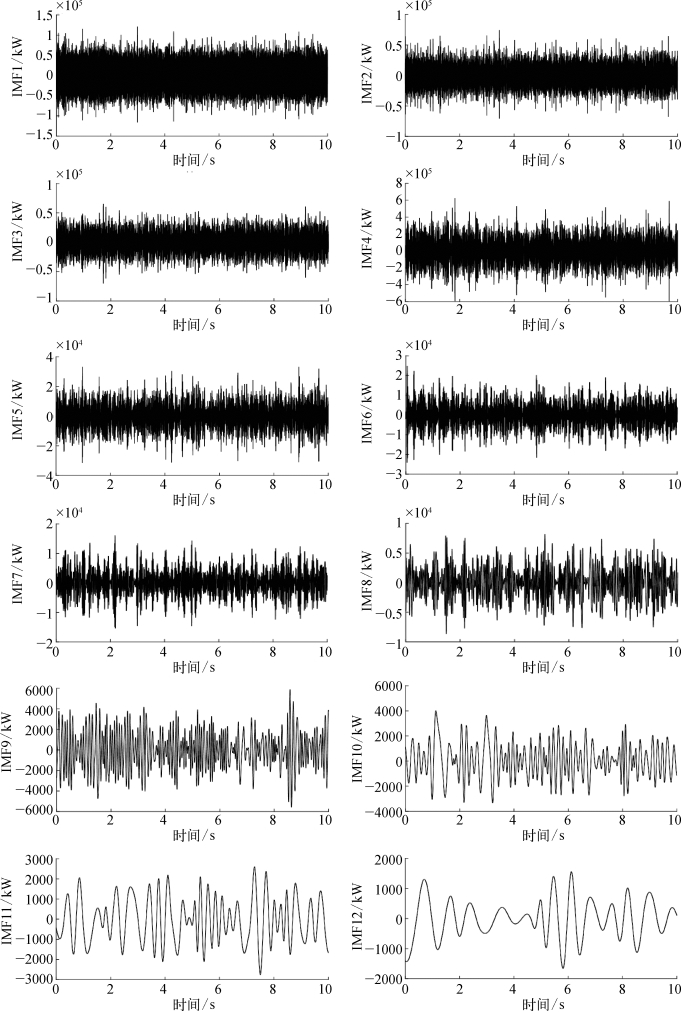
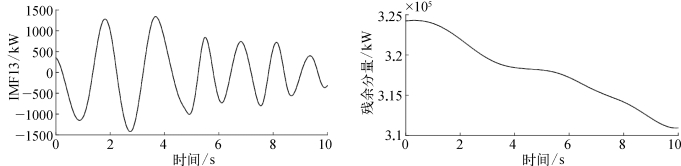
图7.23　原始信号分解后的IMF分量以及残余分量
IMF分量从左至右、从上到下的排列，分别为IMF1～IMF13和残余分量。

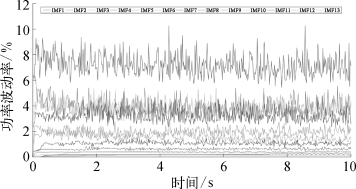
图7.24　输出有用功率的IMF分量功率　波动情况（后附彩图）

此外，每个IMF分量的能量占比情况可参照表7.7所示，输出有功功率的IMF分量的功率波动情况参照图7.24所示。易知，在所有的IMF分量中，分量IMF8～IMF13中的能量占比较少。另外分量IMF5～IMF13的功率波动较小，其基本保持在一个稳定值附近，其对原始信号的影响也较小。故后面的分析重点对分量IMF1～IMF7进行研究。

（2）机网相互作用的振荡模态研究

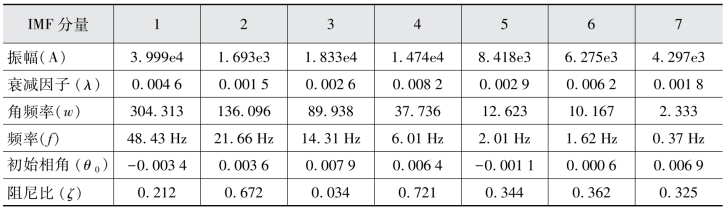
通过对分量IMF1～IMF7进行一定的滤波，然后进行数据拟合，依次可以求出每个分量的振幅（A）、衰减因子（λ）、角频率（w）、初始相角（θ0）、阻尼比（ζ），其结果参照表7.8所示。易知，双馈风电机组的输出有功功率中主要存在以下的四种振荡形式，即为次同步谐振（SSR，21.67）、次同步振荡（SSO，14.32 Hz、2.01 Hz和1.62 Hz）、次同步控制相互作用（SSCI，6.01 Hz）和低频振荡（0.37 Hz）。另外，根据不同振荡模态的初始振幅值可知，次同步控制相互作用比次同步谐振和低频振荡的影响更明显。进一步，次同步振荡比较容易产生于输出功率的信号中。

表7.8　每个IMF分量的特征参数