基于风电大数据FFT分析的振荡识别方法

1.风电大数据的平均值FFT分析

（1）平均值FFT分析方法

实时采集的风电大数据维数较多，且实时更新，数据量非常大。继续采用传统小数据集的直接分析方法将无法完成预期的分析目标。因而，有必要对原始数据进行预处理。对于在风电场采集的电气量（电压值、电流值），在求平均值后，高于同步频率（50 Hz）的谐波频率成分将可以过滤掉，且大多数的间谐波成分也将明显减少。因而，可以按照要求先求取平均值，再对产生的平均值数据集进行频谱分析的方法，分析风电场低于同步频率（50 Hz）的风电场-电网相互作用分析。一般来讲，风电场-电网相互作用的振荡频率点应与特定频段的频谱幅度最大值对应，因而通过查找特定频段幅度最大值对应的频率，即可找到风电场机网相互作用的振荡频率。具体的分析流程方法如下。

第1步：对原始数据进行预处理，全部转化为标幺值；

第2步：对每个周期（0.02 s）计算一次平均电压Ui，平均电流Ii和平均功率Pi等；

第3步：采用带移动时间窗的FFT分析方法对平均值数据进行分析。其中，选用矩形时间窗，时间窗宽度为5 000个数据点（即5 000个周波）。

第4步：将每个时间窗的数据进行特定频段的数据提取。

第5步：通过求取特定频段的极值点，找出频谱幅度最大值点对应的频率。

由于测量的原始数据是按照不同风速段进行数据记录，每个数据段记录了10 min的数据，当对全天（24 h）甚至更长时间的风电大数据进行分析时，需要按照上面的分析流程，循环处理不同的数据段。完整的风电大数据平均值FFT分析的程序流程图如图7.15所示。

由于原始数据采集记录可能存在错误或者空值，在用分析软件（如MATLAB）进行数据分析时，将会造成计算结果为非数NAN的情况，若对含有非数NAN的平均值进行FFT分析，将导致进一步的非数NAN扩散，因而，有必要在计算的平均值结果后增加异常数据（非数NAN）分析处理，检测出非数NAN所在的位置。为了不影响整体的FFT分析效果，一种可行的方案是取前后两个平均值点的均值，代替MALAB计算得出的非数NAN，从而保证平均值频谱分析的顺利进行。

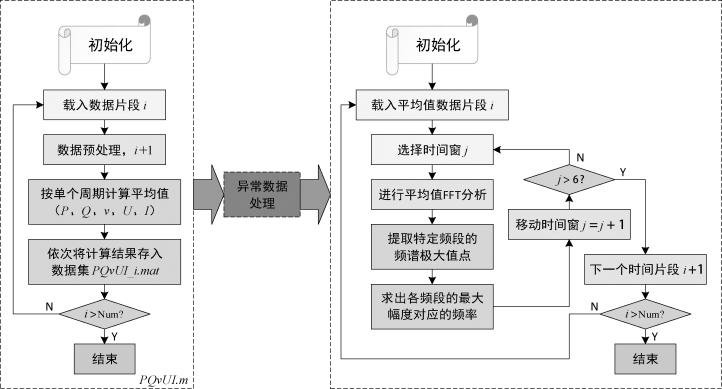
图7.15　风电大数据平均值FFT的程序流程图

一般地，若风电场电压、电流的采样频率为fs，则每个周期有n＝fs／50个数据点，按一个周期时间长度分别取平均值后，平均值数据集的等效采样频率应为

由式可以看出，平均值的等效采样频率不受原始数据采样频率影响。因而，在考虑奈奎斯特频率fn＝fs／2的情况下，平均值数据集可以用于0～25 Hz频段的风电场-电网相互作用的研究。

另一方面，随着风电场持续的并网运行，数据量急剧上升，采用基于平均值的数据分析方法，将有效实现数据降维的作用。按每个周期求取的平均值的方法计算，数据量可以缩小n＝fs／50倍。

（2）实例分析

由于次同步振荡（SSO）主要与轴系转矩强相关，而转矩与平均功率具有线性对应关系，所以可以通过分析平均功率的频谱进行SSO的振荡频率分析；由于SSCI主要与变流器控制装置强相关，而控制装置的输入量中电压受电网电压决定（基本不变），所以可以通过分析平均电流的频谱进行SSCI的振荡频率分析；由于低频振荡与轴系和控制装置都强相关，所以也可以通过分析平均电流的频谱机型低频振荡的频率分析。(www.xing528.com)

基于对2 MW双馈风力发电系统并网的小信号模型和时域模型的分析，对于实时采集的风电大数据（采样频率fs＝4 000 Hz），可取平均功率的1.7～2.2 Hz和12～14 Hz频段进行次同步振荡（SSO）分析；取平均电流的3～8 Hz频段进行次同步控制相互作用（SSCI）分析；取平均电流的0.2～2.5 Hz频段进行低频振荡分析。分别提取以上四个频段0.2～2.5 Hz（电流I），1.7～2.2 Hz（功率P），3～8 Hz（电流I），12～14 Hz（功率P）的细节频谱图进行分析，如图7.16所示。利用MATLAB找出这四个频段的极大值点后，即可筛选出各个频段的频谱最大幅度及其对应的频率值。利用MATLAB分析可得，上述四个频段的最大幅度对应的频率分别为1.95 Hz（功率P）、12.07 Hz（功率P）、0.31 Hz（电流I）、5.01 Hz（电流I）。

图7.16　平均功率P和平均电流I的特定频段频谱图

图7.16仅仅对第一个平均值时间窗（5 000数据点）进行了特定频段的最大幅度及频率进行了分析。由于风速的随机性，平均功率和平均电流的频谱也具有一定随机特征，因而有必要采用数理统计的方法对更多数据进行处理分析，以观察其变化规律。

2.FFT结果的数理统计分析

首先，可以利用箱线图观察最大幅度-频率数据的分布特征，进而对异常值进行分析过滤，如图7.16所示。其中，图7.17（a）和（b）分别为功率P和电流I1的FFT最大幅度-频率数据箱线图，观察可知二者均存在一个远远大于其他值的异常点。通过筛选最大值发现：（a）和（b）中的异常点均为第318个平均值FFT分析时间窗，可能由原始数据采集设备记录错误或者风机启停造成，应予以剔除。（c）和（d）即为去除异常点后的箱线图。

然后，利用条形图统计各个频段子区间的最大幅度-频率点出现的频次，以及各子区间的加权平均值分布。相应的最大幅度-频率点出现频次分布图如图7.18所示，其加权平均值分布图如图7.19所示。其中，以图7.18（a）为例，分别表示区间［1.7 1.75］、［1.75 1.8］、［1.8 1.85］、［1.85 1.9］、［1.9 1.95］、［1.95 2.0］、［2.0 2.05］、［2.05 2.1］、［2.1 2.15］、［2.15 2.2］和［2.2，＋∞）的出现频次。

最后，即可基于获得的各子区间最大幅度-频率点出现频次分布图和加权平均值分布图进行分析，找出最重要的频率点（或者小区间）。

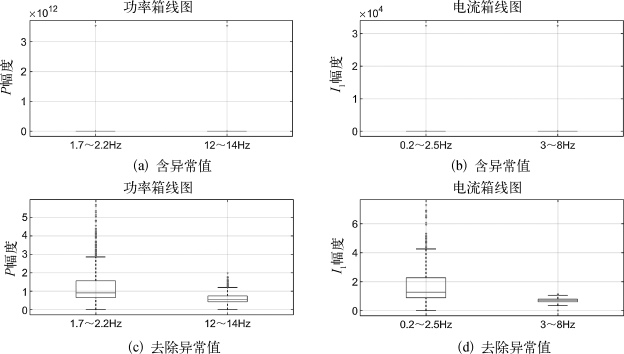
图7.17　最大幅度-频率数据箱线图

图7.18　最大幅度-频率出现频次分布图

将小信号模型分析结果和风电大数据分析结果进行对比，如表7.6所示。该小信号模型是在输入功率（主要有风速决定）恒定，且线路串补度为0.4的条件下进行分析，风电大数据来源于双馈风电场实际采集的数据进行的分析。对比发现，小信号分析所得到的风电场-电网相互作用模态频率与风电大数据分析结果非常接近。在考虑线路串补度的影响后，可以认为风电大数据分析得出的最重要的最大幅度-频率区间中心频率，即为对应的风电场-电网相互作用振荡模态频率。

图7.19　最大幅度-频率加权平均值分布图

表7.6　振荡模态对比分析