HVDC系统的附加阻尼控制器设计

1.HVDC－SSDC对系统稳定性的影响机理

交直流电力系统以及待研究发电机和轴系的小扰动线性化模型如图6.54所示。为了便于下文设计附加控制器，在结构上将直流整流侧的定电流控制独立表示。通过计算该线性化系统的特征值，可以判断次同步振荡的稳定性。

从机理上来讲，直流系统引起整流站附近汽轮机组轴系次同步振荡的原因可以直观地理解为当发电机的频率发生扰动Δω时，在整流器快速控制的作用下，电气系统提供反相位分量的电磁转矩ΔTe，即负阻尼，引发次同步振荡。特征值方法很难诠释次同步振荡的产生过程，利用复转矩系数法中电气阻尼的定义则很容易分析交直流系统对待研究发电机的作用特性。

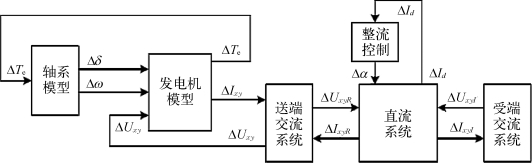
图6.54　交直流系统的小扰动模型结构图

将图6.54中的轴系模型移除，只保留系统的电气部分，系统模型如图6.55所示。以图6.55中发电机频率Δω作为输入变量，发电机电磁转矩ΔTe作为输出变量，电气阻尼系数可以表示为

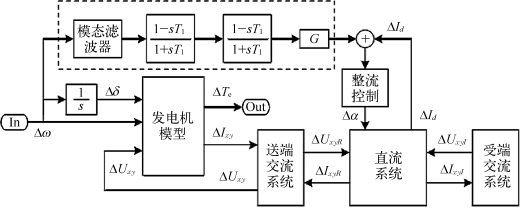
图6.55　SSDC的基本结构

SSDC影响系统稳定性原理是在HVDC整流控制上叠加一个附加传递函数，使得电气系统在待抑制的次同步振荡频率范围内另外提供适当的正阻尼。SSDC的结构如图6.55中虚线框内所示，其输入信号为发电机的转速Δω，输出信号与整流基本控制的输入信号相叠加。

SSDC有三个基本环节：①模态滤波器，其作用是根据分离模态设计原则，使SSDC仅对转速信号Δω中的待抑制次同步模态分量起作用，避免SSDC对系统其他模态产生负面影响；②相位补偿环节，其作用是调节SSDC所补偿电磁转矩的相位，使之与发电机转速的相位差在0°左右，为次同步振荡补偿正阻尼；③增益G，其作用是调整SSDC附加阻尼的倍率。

2.HVDV-SSDC的机网相互作用抑制策略及效果分析

（1）SSDC参数整定方法

SSDC的模态滤波器可采用Butterworth结构，阶次取2阶即可，中心频率一般取次同步振荡模态频率，带宽一般取1～2 Hz。如果相邻的两个次同步振荡模态频率靠得很近（小于2 Hz），由于相近模态的最佳相位补偿值基本相等，因此可以利用一个SSDC回路同时阻尼控制这两个模态。

从线性化系统输入输出频率响应的角度来讲，图6.55中输出ΔTe对输入Δω的响应等于ΔTe对发电机模型输入Δω响应与ΔTe对SSDC输入Δω响应之和。SSDc相位补偿环节的最佳补偿相位可以通过图6.56所示的系统模型计算得到：

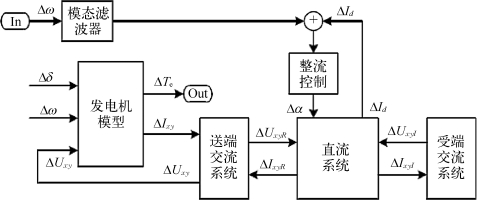
图6.56　用以计算补偿相位的系统模型结构图

其中，h为次同步振荡模态中心频率，单位为rad/s；Phase（jh）为h点的相频响应；Mod表示取模运算；Pc为相位补偿环节的最佳相频响应，单位为°，其值域为（－360，0］。(www.xing528.com)

相位补偿环节的最佳时间常数T1可以表示为

SSDC中增益G越大，抑制次同步振荡的效果越好，但G太大也可能会影响系统其他模态的稳定性，同时控制器输出也更容易达到限幅环节的极大极小值。因此，调节G使得次同步振荡模态具有适当的阻尼比即可。

（2）SSDC有效性验证

以并网系统所含HVDC系统进行仿真验证，其中，仿真设置整流侧的发电系统采用孤岛运行方式。当HVDC整流侧触发角α＝18°时，次同步振荡的第1模态（f1＝17.85 Hz）和第2模态（f2＝32.43 Hz）均不稳定。

针对次同步振荡第1模态和第2模态分别设计SSDC。模 态1的SSDC参 数 为；模态2的SSDC参数为。安装SSDC前后系统的电气阻尼曲线如图6.57所示。由此可见，SSDC可以有效提高次同步振荡模态1和模态2的电气阻尼，抑制系统的次同步振荡。

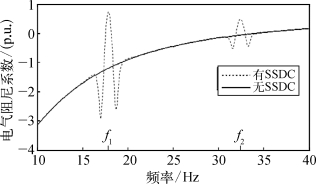
图6.57　安装SSDC前后系统的电气阻尼

（3）基于BP神经网络的自适应SSDC设计

对多源系统中2 400 MW火电机组设计自适应SSDC抑制系统的次同步振荡。其轴系扭振模态1（13.45 Hz）和模态2（24.73 Hz）均可能产生不稳定的次同步振荡。为便于研究，设轴系机械阻尼为0，设计自适应SSDC抑制次同步振荡模态1。

首先采用之前设计方法，考虑功率P和触发角α在一定范围变化，离线确定一系列最佳SSDC参数作为神经网络的学习信号。然后以直流整流侧的功率P和触发角α为BP神经网络的输入信号，以SSDC的相位补偿环节时间常数T1和增益环节G为输出信号，建立一个BP神经网络。神经网络采用一个Sigmoid型隐含层和一个线性输出层，隐含层采用4个神经元。时间常数T1的期望误差取为0.000 1 s，增益G的期望误差取为0.01。对神经网络进行训练后，即可将神经网络投入系统，含神经网络自适应SSDC控制器的系统结构如图6.58所示，其中GΔω为2 400 MW火电厂发电机的转速角频率。

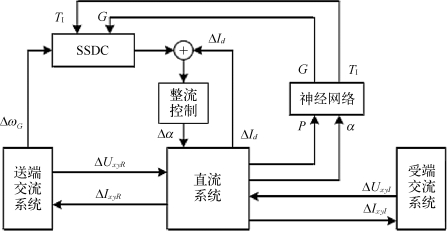
图6.58　基于神经网络的自适应SSDC

以整流侧触发角α＝15°、直流输送功率P＝1.0 p.u.（2 700 MW）的系统正常运行工况为基础，设计固定参数SSDC。然后分别将固定参数SSDC和神经网络自适应SSDC投入系统，利用PSCAD进行时域仿真，比较两种控制器的效果。在正常运行工况下，两种控制器的效果基本一致，但系统运行状态发生不利于SSO稳定变化时，固定参数的控制效果不尽如人意。

PSCAD仿真程序的设置为第5 s在火电厂母线发生单相对地故障，0.02 s后清除故障，在第9 s投入SSDC，采用模态滤波器观测第2质量块和第3质量块之间扭矩的模态1分量。图6.59分别给出 了P＝1.25 p.u.、α＝15°和P＝1.0 p.u.、α＝30°时两种控制器抑制次同步振荡的实际效果。由图可见，当直流输送功率增大25%后，定参数SSDC虽然仍然可以抑制SSO，但轴系扭矩收敛速度较慢。当触发角α增大为30°后，定参数SSDC的投入可以降低轴系扭矩的发散速度，但达不到抑制SSO的效果。基于神经网络的自适应SSDC在两种工况下都可以较好的抑制SSO，使轴系扭矩的模态1分量较快收敛。

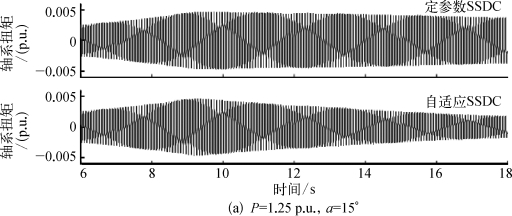
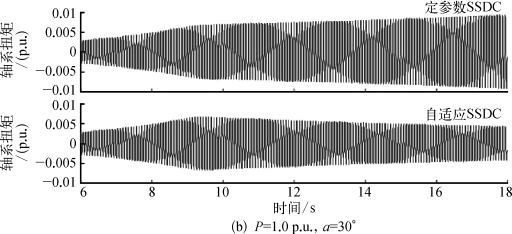
图6.59　投入SSDC前后的轴系扭矩