SVC对机网相互作用的抑制作用优化建议：SVC对机网相互作用的有效抑制

1.SVC的工作原理

将SVC通过专用变压器连接到被保护发电机组出口母线上SVC是抑制次同步振荡的典型的接线方式，该SVC仅由晶闸管控制电抗器（TCR）组成，并装设滤波器，专用多绕组变压器抵消了SVC产生的部分高次谐波电流。SVC控制器的输入信号为含有发电机组轴系扭振模态频率的量，通过控制晶闸管的触发延迟角α，改变晶闸管控制电抗器支路电流的大小，调节发电机组的电磁功率，产生阻尼转矩来抑制次同步振荡。

当系统没有发生次同步振荡时，应选择合适的静态工作点和滤波器参数，使SVC装置的参数配合达到最佳抑制效果，并降低SVC对电力系统的不良影响。SVC引入的0.1～2 Hz在惯性频率范围内的阻尼可以提高系统输送能力的控制，引入的在系统较高的扭振模态频率5～45 Hz的范围内的阻尼可以抑制系统次同步振荡。

SVC通过注入电压来提高暂态稳定性、改善振荡阻尼特性等。把晶闸管控制电抗器与被保护发电机的机端母线并联，通过调节其电流来抑制次同步振荡。晶闸管控制电抗器的电纳值与触发角有关。确定了电抗器的额定电感值后，TCR的等效电纳值可以通过调节控制触发角的大小而改变。触发角与补偿电抗器的支路电纳值关系如下：

式中，α为晶闸管控制电抗器的触发角；L1为支路电感值。

控制器的输入信号为含有原动机扭振模式分量的测量值，通过控制晶闸管的触发角来调节晶闸管控制电抗器支路电流的大小，调节发电机的输出功率，产生阻尼转矩来抑制次同步振荡。高压杠速度偏差、输出功率等信号都含有需要阻尼的所有原动机的扭振模式分量。由于这两种信号对控制器的相移更敏感，因此，为提高SVC的控制效果，控制器的输入信号选择发电机的转速偏差。

控制器的输入信号为转速偏差信号时，晶闸管控制电抗器中的无功电流应与发电机转子速度偏差反相。当转速减小时，晶闸管控制电抗器的感性电流增大了，机端电压减小，发电机送出的电磁功率减小，发电机转子的速度增加。反之，发电机的转子减速。因晶闸管控制电抗器的控制速度快，所以能够抑制次同步振荡。晶闸管控制电抗器TCR起到可变电感的作用，它所吸收的感性无功功率可以快速、平滑地调节。晶闸管控制的电抗器简化基本结构就是一个电抗器TCR和两个反并联的晶闸管串联。

因为电感具有储能作用，在晶闸管控制的电感电路中，晶闸管一旦导通，只有当回路电流大于零时才能关断。延迟关断的时间不仅与触发角有关，还与电源电压和回路电流间的相位角（或称电路阻抗角）有关。因此，对于双向开关来说，在其中一个晶间管还没有关断的情况下，不可能触发另一晶闸管导通。在这种情况下应采用宽脉冲或脉冲列触发方式，以保证两个晶阐管的正常工作。两个晶闸管的触发延迟角取值也应相同，以避免正负半周波形不对称而产生的偶次谐波和直流分量。由于假定电抗器为纯感性的，故触发延迟角的有效移相范围是90°～180°。

晶闸管控制的电抗器TCR支路中，当晶闸管完全导通时，触发延迟角α＝90°，导通角θ＝180°无功功率流和吸收的基波电最大，流过电感的电流呈正弦波形。当晶闸管部分区间导通时，触发延迟角α在90°～180°，导通角θ＜180°。当α角增大时，其等效电纳减小了，即增大补偿器的等效电抗，因此其吸收的无功功率减小了。

从以上的分析中可以得到，通过改变晶闸管可控电抗器的触发延迟角90°＜α＜180°可以控制回路中的电流，晶闸管控制的电抗器TCR起到了可变电感的作用，它所吸收的感性无功功率可以在零到最大值间快速、平滑地调节。

当次同步振荡发生时。向机组电枢注入与轴系次同步扭振频率互补的电流可以抑制次同步振荡。而在相控原则下。控制变量与SVC的次同步频率电纳之间没有直接联系。很难通过改变α角来控制SVC的次同步频率电纳；在次同步振荡发生时。工频电纳数量与SVC的次同步频率电纳相同。而工频电压远远超过发电机端母线电压的次同步频率分量。所以，产生的次同步频率的电流远低于工频电流，难以通过改变次同步电纳来产生互补的次同步频率电流。因此，本节将着重分析次同步频率调制的控制原理。通过调节SVC的基波电纳产生与发电机组轴系扭振模态频率互补的电流分量。进而在发电机组中产生相应模态阻尼转矩以达到抑制系统次同步振荡的目的。

当次同步振荡发生时，SVC的母线电压有很多不同频率的分量，此外，还在SVC的特征谐波电流两侧产生了谐波电流，其幅值远远低于与工频电压下的次同步频率电流。通过仿真模型对SVC基波电纳控制原理进行了验证，可以用60 Hz恒频率电源代替，把28 Hz的次同步频率分量叠加在SVC的基波导纳上，来消除频率电压分量的影响，图6.26为SVC基波电纳次同步调制输出电流的频谱分析。

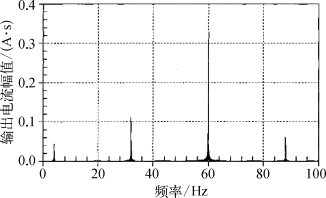
图6.26　基波电纳次同步调制输出　电流频谱分析图

由图6.26可知，采用28 Hz的次同步频率对SVC的基波电纳进行调制，在其输出电流中含有的88 Hz超同步频率分量和32 Hz次同步频率分量，其中，采用抑制系统次同步振荡需要的电流分量是32 Hz。

取各模态频率的ωm，对SVC的基波电纳进行次同步频率的调制，SVC的输出电流包含次同步频率为（ω1－ωm）和超同步频率为（ω1＋ωm）的电流分量，而进入发电机定子的以次同步电流为主，改变基波电纳的调制信号的初相位和幅值，在机组轴系形成了合适的次同步阻尼转矩，从而达到抑制次同步振荡的目的，这就是SVC抑制次同步振荡的原理。

系统发生次同步振荡时，发电机定子上感应的扰动电压有两个频率不等的分量，它们分别为次同步频率分量和超同步频率分量，前者与轴系扭振频率互补，在线性系统中，采用叠加定理能够分别求出系统的超同步和次同步扰动的电流分量。

当转速偏差Δω与发电机转子的电磁转矩的相位差在－90°～＋90°之间时，次同步频率转矩会使发电机的转速振荡增强。尤其当与转子自然扭振频率互补的次同步频率为电气系统的谐振频率时，该负阻尼将达到最大值，发电机组在该振荡模式下将存在严重的次同步振荡问题。

在谐振频率点，如果发电机转速偏差与SVC产生的次同步频率电流互成180°，即二者相位相反时，能够在发电机转子的自然扭振频率点产生最大的阻尼转矩。所以，在设计SVC的控制装置时，为了保证在相同容量的情况下SVC的阻尼效果最佳，需要按照这种反相位的原则进行相位补偿环节的设计。

2.SVC中的附加阻尼控制器设计

（1）相位补偿环节参数设计

SVC是一种并联型无功补偿设备，由晶闸管控制并联电抗器和晶闸管投切并联电容器组成。在SVC中引入次同步阻尼控制器可以为系统提供正的电气阻尼，从而对次同步相互作用起到抑制作用。在风电场出口并联的SVC中附加次同步阻尼控制器，对不稳定模态进行抑制，如图6.27所示。将直驱风电场输出的有功功率偏差ΔPg作为SSDC的输入信号。为了使SSDC在抑制系统次同步相互作用的同时不对系统的稳态特性造成影响，在SSDC作用通道上增加一个限幅环节，使SSDC输出信号受限幅环节的限制。SSDC输出信号经限幅环节后得到的信号Δα为SVC的触发角增量。

(www.xing528.com)

图6.27　SVC－SSDC的作用原理图

未加SSDC时，以SSDC输出信号的注入点为输入，以SSDC的输入信号为输出的开环系统的伯德图如图6.28所示，其中伯德图中的频率范围为5～25 Hz。可以通过图6.28中的开环系统的伯德图中的对数幅频特性曲线和对数相频特性曲线得到该系统在特定频率下的幅频特性。通过伯德图中的对数相频特性曲线得到为－308°，由于SSDC中相位补偿环节之外的其他环节在次同步振荡频率的相位和为0°，可计算得到SSDC的补偿相位为308°，此时对应的相位补偿环节的时间常数T＝0.003 3。

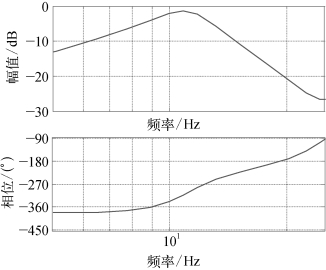
图6.28　未加SSDC时开环系统伯德图

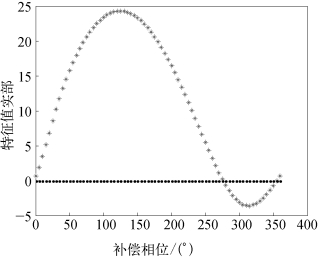
图6.29　补偿相位和受控模态特征值实部关系曲线

为了验证SSDC补偿相位设计方法的正确性，在比例环节参数取1.5的基础上，次同步阻尼控制器的补偿相位从0°～360°递增，其中相位补偿环节的时间常数T可以通过补偿相位计算得到。得到受控模态的特征值实部与补偿相位之间的关系曲线，如图6.29所示。

从图6.29可以看出，当次同步阻尼控制器的补偿相位从0°～360°递增时，受控模态的特征值呈现出增大，后减小，再增大的趋势。当次同步阻尼控制器的补偿相位从0°～120°递增时，受控模态的特征值实部持续增大。当次同步阻尼控制器的补偿相位从120°～308°递增时，受控模态的特征值实部持续减小。当次同步阻尼控制器的补偿相位从308°～360°递增时，受控模态的特征值实部持续增大。当次同步阻尼控制器的补偿相位在285°～340°范围内时。受控模态的特征值实部为负值，此时系统稳定。

从图6.29可以得到，当补偿相位为308°时，受控模态特征值实部最小，对应的阻尼比最大，此时补偿效果最佳。当补偿相位在308°附近取值时，受控模态也具有较大的阻尼比，此时也具有较好的补偿效果。因此采用遍历的方法取得的最佳补偿相位与理论结果一致，因此相位补偿环节参数设计方法的合理性得到验证。

（2）比例环节参数设计

通过图6.28中的对数幅频特性曲线可以计算得到为0.854，由此计算得到次同步阻尼控制器的临界增益为1.17。因此根据SSDC比例环节参数设计方法，SSDC的比例环节参数应取大于1.17的合理值。

为了验证次同步阻尼控制器比例环节参数设计方法的正确性，在补偿相位确定的基础上，取比例环节的参数K分别为0.80，1.00，1.17，1.40，1.60，对比补偿后受控模态的阻尼变化情况，具体结果如表6.8所示。

表6.8　K变化对模态的影响

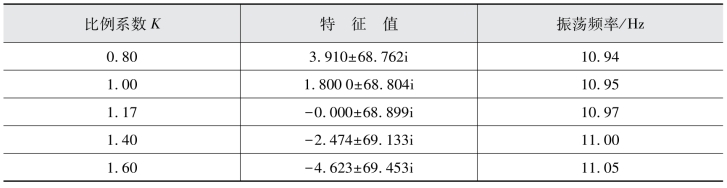
从表6.8可以看出，当K的取值为0.80和1.00时，受控模态的特征值实部大于0，此时系统不稳定。当K的取值为1.17时，受控模态的特征值实部等于0，系统处于临界稳定状态。当K的取值为1.40和1.60时，受控模态的特征值实部小于0，此时系统稳定。随着K取值的变化，受控模态对应的振荡频率在11 Hz附近有小幅度的变化。

当K的取值为0.80时，对应的开环系统ω从0→∞变化时的奈奎斯特曲线如图6.30所示，奈奎斯特曲线穿越负实轴（－∞，－1）段的次数为0，由于附加SSDC前的系统有1个不稳定模态，所以根据奈奎斯特稳定性判据，此时闭环系统不稳定。

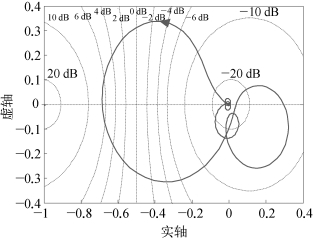
图6.30　K＝0.80时的奈奎斯特曲线

当K的取值为1.17时，系统对应的开环系统ω从0→∞变化时的奈奎斯特曲线如图6.31所示，奈奎斯特曲线正好经过（－1，j0），根据奈奎斯特稳定性判据，此时闭环系统处于临界稳定的情况。当K的取值为1.60时，系统对应的开环系统ω从0→∞变化时的奈奎斯特曲线如图6.32所示，奈奎斯特曲线穿越负实轴（－∞，－1）段的次数为1，由于附加SSDC前的系统有1个不稳定模态，所以根据奈奎斯特稳定性判据，此时闭环系统稳定。

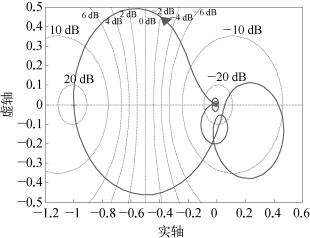
图6.31　K＝1.17时的奈奎斯特曲线

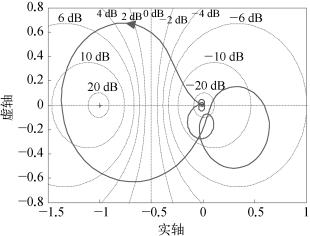
图6.32　K＝1.60时的奈奎斯特曲线

当K小于1.17时，系统不稳定；当K大于1.17时，系统稳定。因此，SSDC比例环节参数K应取大于1.17的合适值。比例环节参数设计方法的合理性得到验证。