风电机组阻尼控制器的优化设计

1.风电机组对次同步轴系相互作用的转矩阻尼控制

维持风电机组传动轴系统较高的阻尼水平对于提高风电机组可靠性以及保证电力系统安全稳定运行具有重要意义。为提高风电机组轴系振荡阻尼，近年来国内外学者已对此开展了相关的研究。

变速变桨距风电机组的控制系统如图6.23所示，该控制系统包括转矩-转速控制环和桨距-转速控制环。为了提高风能利用效率，在低于额定风速下，转矩控制器通过调整发电机转矩来控制发电机转速，即转矩-转速控制环起作用，获得最优的叶尖速比从而提高气动扭矩效率。另一方面，当风速高于额定风速时，发电机转矩应当一直处于额定的最大值，通过桨距调节来控制气动转矩使涡轮处于额定转速，即桨距-转速控制环起作用。

图6.23　变速变桨距风机转速控制环

如图6.23（b）所示，桨距－转速控制器通过控制叶轮捕获的风能使得风力机在额定状态下运行，从而控制发电机转速在适当的范围。桨距角控制器包括一个PID控制器，由此可以通过发电机转速偏差得到参考桨距角βref。为了取得更好的控制效果，PID控制器在设计时应当具有良好的相应速度。常见的两种阻尼器，分别为仅包含传动轴振荡模态的阻尼器和包含轴系与桨叶弹性的三质量块振荡模态的阻尼器。

针对变速变桨距风电机组的转矩阻尼控制策略，主要有①根据转矩控制环要求，设计转矩阻尼控制器，运用RBF神经网络控制方法实现转矩控制系统的PID参数的自寻优整定，由于传动链阻尼的设计，可有效减小齿轮箱振荡扭矩，减小外界干扰对传动链的冲击，延长机组寿命，并使系统有很好的动态性能和稳定性；PID参数的自寻优，使得转矩控制器在额定风速下很好地跟随最大Cp曲线，达到预期控制效果。②根据双馈风电机组闭环系统电磁转矩-转速微增量的表达式，得到电气阻尼转矩系数与机组有功控制策略、运行状态以及控制系统参数之间的定量关系，设计基于双馈电机转速信号的扭转振荡阻尼控制器，根据电磁转矩－转速相位特性确定合适的补偿相位并设计阻尼控制器参数。

2.风电机组对次同步轴系相互作用的附加阻尼控制

本节提出一种对网侧电气小扰动引发机网扭振的抑制策略。该策略通过在转子侧逆变器功率控制环节引入阻尼器，当轴系发生扭振时，利用发电机转速波动信号产生阻尼功率，再附加到逆变器有功功率参考值上，使系统额外输出有功功率来增大系统阻尼，从而抑制轴系扭振。

（1）附加阻尼控制对稳定性的影响机理

由于机械轴上的扭矩振荡本质为有功功率的振荡，为了能够在轴系发生扭振时提高系统阻尼，可以考虑在扭振发生时，让风机附加输出一个与扭振功率相位相反、幅值相当的附加阻尼功率，起到抑制扭振的作用。这种提高阻尼的办法可以通过在有功功率控制环路中引入扭振阻尼器来实现，阻尼器通常由滤波器和相位补偿环节构成，滤波器的作用是当异步电机输入机械扭矩发生振荡时，将其振荡频率提取出来，相位补偿环节在滤波的基础上提供相位补偿，使发电机输出的附加阻尼功率与目标抑制功率相位相反。当轴系发生扭振时，发电机转速波动与输入机械转矩波动之间的关系如下式：

可见，发电机转速的变化能够反映机械扭矩的波动，因此，阻尼器的输入为发电机机械转速，经过滤波器后，转速波动被提取，再经过增益放大和相位补偿，阻尼器输出附加阻尼参考功率。

这里采用基于低通滤波器设计的阻尼器，相比传统窄带宽阻尼器具有更大的低频带宽，在振荡模态不止一种的复杂情况下，无需针对每一个目标抑制频率都设计一个滤波器，具有设计简单，计算量小等优势。基于低通滤波器的阻尼器结构示意图如图6.24所示。

图6.24　基于低通滤波器的振荡阻尼器

此处采用典型的二阶低通滤波器，低通滤波器传递函数如下：

ωc为截止频率，Q为品质因数，Q越大由截止频带向阻带过渡越快，但品质因数过大会导致在截止频率处的幅值超调，此处设定Q＝0.707，即滤波器具有平滑的巴特沃兹响应。阻尼器的输入信号为发电机转速，低通滤波器的截止频率取小于轴系固有振荡频率，从而通过低通滤波器后能够得到转速直流分量，输出的直流信号与测得的转速信号做减法运算得到转速波动信号，该信号能够实时反应转矩的振荡情况，再经过增益放大后得到与振荡功率幅值相当的阻尼功率参考值，叠加到转子侧有功功率参考值上，当扭振发生时，附加阻尼控制能够使逆变器输出额外的阻尼功率，起到抑制转矩振荡的作用。通过以上分析可得转子侧逆变器附加阻尼控制框图，如图1.10（a）所示。

值得注意的是，此处合理假设阻尼器的响应延迟相比于整个转速功率控制环路的响应时间要小得多。因此，扭振发生时，转子侧变流器能够及时地响应输出阻尼功率，后续的仿真也验证了假设的正确性。根据图1.10（a）和式（6.30）可得阻尼器转速功率传递函数，如式（6.32）所示。

其中，ζ＝1／2Q，定义为阻尼比。为了建立振荡阻尼器的小信号模型，根据式（6.32），引入中间状态变量x1和x2，阻尼器的状态表达式为式（6.33）。

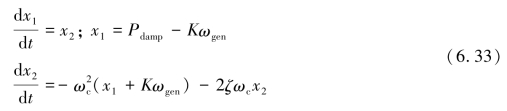(www.xing528.com)

为了建立转子侧变流器控制方程的小信号模型，图6.25给出了带有PI控制参数的控制框图。

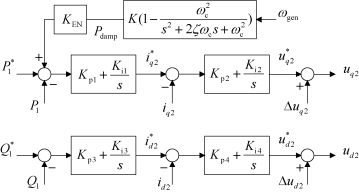
图6.25　转子侧变流器控制框图对应传递函数

同样引入状态变量x3，x4，x5，x6和控制变量KEN，KEN＝1表明系统引入阻尼器，附加阻尼控制起作用，当KEN＝0表明阻尼器不起作用；于是，图6.25控制框图的状态方程可表示为式（6.34）。

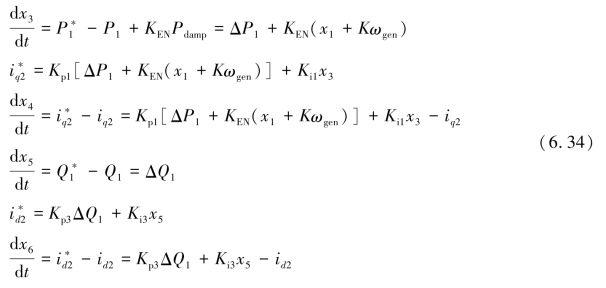
变流器的输出为转子电压：

整理成矩阵方程形式，转子侧变流器控制小信号模型如式（6.36）所示。

其　中　状　态　变　量xRSC＝［x1，x2，x3，x4，x5，x6］T，　输　入uRSC＝［ΔP1，ΔQ1，ωgen，id2，iq2，ψ1］T，输出yRSC＝［uq2，ud2］T，状态矩阵为

（2）附加阻尼控制对机网相互作用的抑制策略及效果分析

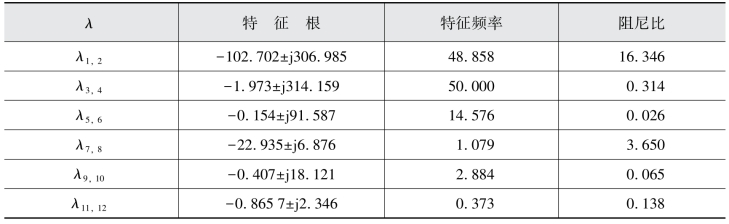
为了研究转子侧附加阻尼控制对系统阻尼的影响，首先计算无阻尼附加控制的系统的共轭特征根，计算这些振荡模态与机械传动轴相关状态变量的相关因子。然后计算带有附加阻尼控制的系统的特征根，再次观察轴系扭振对应的振荡模态的阻尼情况，如果特征根实部绝对值变大，说明轴系扭振的阻尼特性提高，附加阻尼控制确实有效增大了系统阻尼。值得注意的是，本书在此只研究与轴系扭振相关的振荡模态，为了方便研究，简化计算量，本节只关注与轴系相关的状态变量，即xmech＝［θ1，θ2，θ3，ωrot，ω2，ωgen］T，也只计算振荡模态与该组状态变量的相关因子。表6.5给出了系统无附加阻尼控制情况下所有含有振荡模态的特征根，其他特征根均为单个的负实数，表明系统是稳定的，这里不予列出。同时，从中可以看出，低速轴扭矩角θ2和低速轴转速ω2主导λ5，6对应的振荡模态，因此λ5，6代表了轴系扭振的一个机械振荡模态，即低速轴振荡模态；同理可见λ9，10代表了轴系扭振的另一个机械振荡模态，即高速轴振荡模态。

表6.5　馈风机小信号系统的振荡模态_____________________________

表6.6计算了这些振荡模态与轴系相关的状态变量的相关因子，其中加粗的参与因子值表明这组振荡模态与所对应的状态变量高度相关。

表6.6　振荡模态与轴系状态变量的相关因子

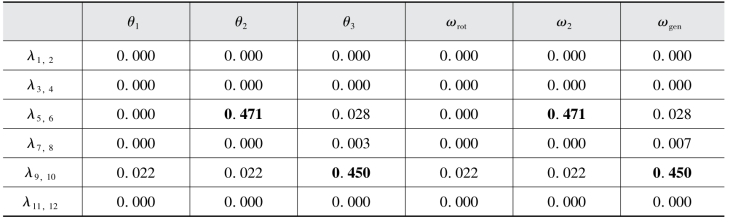
从表6.6可以看出，低速轴扭矩角θ2和低速轴转速ω2主导λ5，6对应的振荡模态，因此λ5，6代表了轴系扭振的一个机械振荡模态，即低速轴振荡模态；同理可见λ9，10代表了轴系扭振的另一个机械振荡模态，即高速轴振荡模态。

接着观察带有附加阻尼控制系统的特征根λ5，6和λ9，10的阻尼情况。可以看出λ5，6和λ9，10的阻尼比有不同程度的增长，附加阻尼控制对提高低速轴振荡模态λ5，6的阻尼有限，从0.025增大到0.026；而对于高速轴振荡模态λ9，10，阻尼比显著增大，从0.005提高到0.065。因此，附加阻尼控制可以有效地增大双馈风机系统轴系的阻尼。

表6.7　带有附加阻尼控制的系统振荡模态