风电机组变流器控制参数对机网相互作用的抑制作用

以双馈风电机组为例，分析其变流器PI参数对机网相互作用的影响及优化方法。

1.PI参数变化对稳定性的影响

根据第3章对双馈风电机组振荡模态的分析，共存在电气谐振、SSR、SSO、SSCI和低频振荡五种振荡模态，各种振荡模态详细信息如表6.1所示。

表6.1　双馈风电机组连接至无穷大电网的各种振荡模态

其中与变流器控制PI参数紧密相关的有SSO、SSCI和低频振荡三种振荡模态，接下来可分别针对不同的PI参数进行讨论。为了研究各控制模块的PI参数变化对系统各个振荡模态的影响，依次改变各PI参数，保持其他变量不变，得到系统各种振荡模态下所对应的阻尼比的变化。分析的结果可参照第3.6.1节，通过分析结果可以得到变流器参数改变时，各种振荡模态的变化趋势和稳定性。基于此考虑各个振荡模态最佳PI参数的选取方法。

2.基于PI参数的机网相互作用抑制策略

1）抑制机网相互作用的多目标优化模型

以PI参数的取值作为优化目标。表6.2为实际工程中采用的PI参数，这组参数可以使并网DFIG系统保持稳定，但这组PI控制器参数并非最佳。为了改善系统的动态性能，仍然需要采用一种有效的方法，该方法可以选择适当的控制器参数以增加振荡模式的阻尼比。结合小信号模态分析，本书以最大化DFIG系统的阻尼比为目标建立多目标优化模型，抑制并网DFIG系统的机网相互作用。

基于特征值分析方法，特征值的实部必须为负，以确保稳定性。此外，为便于计算，PI控制器参数允许的值范围是第二部分中设定值的1/10到10倍。综上，抑制机网相互作用的多目标优化模型的目标函数及其约束是如式（6.10）所示。

表6.2　PI控制器的参数

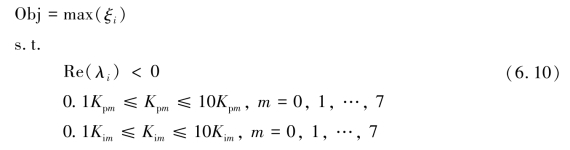
2）模型求解

NSGA-III是一种有效的多目标优化进化算法，其关键是将优势准则和参考点与遗传算法相结合，在解空间中找到非支配解。NSGA-III的流程框图如图6.8所示。就本书中的优化问题而言，其详细的实现步骤如下所述：

（1）每个群体的个体都由16个变量组成，即表1中的PI控制器参数。初始群体由个体构成，其通过随机分配到允许范围内的变量形成。

（2）通过第2部分中的小信号模型、适应度函数和初始父代种群中的数据的组合来计算初始父代种群的12个适应度值。

（3）通过非支配排序将种群进行分类并按照升序排序。此外，考虑到约束Re（λi）＜0，Re（λi）＜0之和越小，个体的等级越高。

（4）将目标标准化，创建参考点，将每个个体与参考点相关联，并计算参考点的“小生境数”。

（5）为了产生能够保持优势和多样性的新子代种群，该模型将竞争选择，模拟二元交叉（simulated binary crossover，SBX）和多项式变异（polynomial mutation）应用于父代种群。

（6）重复步骤（2）、（3）、（4）以获得适应度值，前排和“小生境数”。

（7）根据前排和“小生境数”，从最后一个种群和步骤5中构建的种群中选择适当的个体以形成下一个种群。

（8）执行步骤（5）、（6）和（7）的循环，直到生成的数量达到上限。

由于提出的优化模型与最终解决方案相对应的目标是高维的，这增加了直观观察和评估算法结果的难度。采用t-SNE方法来减小目标的维数，并对结果进行严格的结构分解。

t-SNE的核心概念是将高维空间中的数据点映射到低维空间，并保持数据点之间的空间距离不变，即在高维空间中近/远的点仍然接近/远在低维空间。

图6.8　NSGA-III的流程框图

假设在高维空间中存在X＝｛x1，…，xN｝数据集，并且xa和xb之间的条件概率pb｜a可以通过高斯函数来测量：

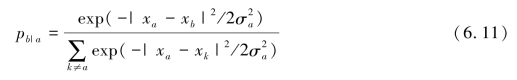
xa和xb之间的相似性（距离）定义为

同样，t-Distribution用于计算低维映射数据点ya和yb之间的相似性：

KL差异（Kullback－Leibler divergence）是衡量2个概率分布一致性的常用方法。KL差异给出了评估两个不同空间维度中数据分布之间关系的成本函数：

(www.xing528.com)

通过最小化成本函数可以获得低维空间中的最佳数据点。很明显，每一个种群都有十二个目标。使用t-SNE算法对每一种群的个体进行可视化分析，如图6.9所示。模型求解流程如图6.10所示。

图6.9　降维示意图

图6.10　优化算法流程图

通过小信号分析及相关因子分析可知，与变流器PI参数相关的模态有λ8，9、λ10，11、λ13，14、λ15，16、λ17，18和λ19，20。因此构建优化目标函数通过小信号模态分析后，构建优化目标函数及约束如式所示：

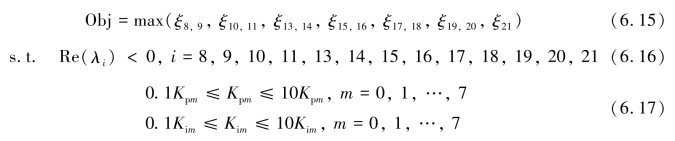
通过前述NSGA-III算法对上述优化模型进行求解，并采用t-SNE算法对结果进行降维可视化。其中NSGA-III采用以下参数：

（1）种群个体数目：200；

（2）种群数量上限ngenmax：100；

（3）交叉率为90%，突变率为50%，其余个体通过重组获得；每个个体至少包含一种不同的基因；

考虑到之前的结论，两种模式λ15，16和λ17，18与PI控制器参数密切相关，认为每个种群的基本个体数量为两个，然后可以在二维平面中映射每一代的Pareto Front，这是对PI参数变化的目标发展趋势的直观观察的基础。此外，二维图有助于PI参数的最佳范围的推广。

经过t-SNE算法降维后，第1代和第10代到第100代（间隔10代）的Pareto Front如图6.11所示。其中颜色条代表群体代数。从图中可以看出，在优化过程中，低维空间中的高维对象的映射会聚在某些固定区域中。剔除分散的数据后，标有黄色圆圈的第100代的目标聚集在一起形成几个黄色区域，这对应于PI参数的最佳范围。

图6.11　第1代……第100代的非支配解降维过程图（后附彩图）

因此，除了第100代个体偏离固定聚合区域的非支配解，第100代的个体的非支配解的PI参数构成的PI参数的最佳范围，如图6.12所示。横坐标表示PI参数，PI参数的值被转换为标准值，其中每个PI参数的基值是其在表6.12中的初始值。图6.11、图6.12和表6.3总结了PI参数的最佳范围。图6.12 PI控制器参数的最佳范围中的纵坐标表示的是PI参数数值。特别地，由于Ki4，Ki6和Ki0分散在整个区域，将其原始参数视为最佳参数。优化前后振荡模态的阻尼比变化如图6.13所示。

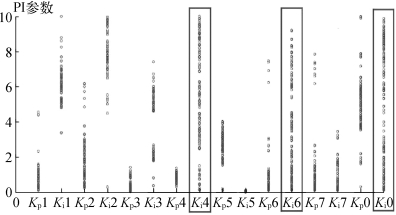
图6.12　PI控制器参数的最佳范围

图6.13　优化前后部分振荡模态阻尼比变化图

从图6.13中可以看出，包括次同步振荡、次同步谐振和低频振荡在内的机网相互作用模态对应的阻尼比均得到了改善，表明本书所采用的通过优化PI控制参数的方法可以增大双馈风电机组中的机网相互作用振荡模态的阻尼比，有效抑制机网相互作用。由于PI控制参数之间存在着相互耦合，本书所采用的优化方法的目标并非使所有模态的阻尼比最大化，而是旨在找出合适的PI参数以抑制工程上关注的那些机网相互作用模态。

表6.3　PI控制器参数的最佳范围值

（3）最优PI控制器参数的适用性分析

为了研究最佳PI参数对不同输出功率的DFIG系统的适用性，本书在前述基础上研究了输出功率变化时特征值的轨迹变化，结果如图6.14所示。本书在小信号模型中将输出功率从0.1 p.u.增加到1 p.u.。PI参数基于表6.3中所示的优化控制器参数范围，具体仿真数值取其中间值。仿真结果表明，在输出功率增加时，只有λ15，16、λ17，18和λ19，20发生变化。

图6.14　功率增加时特征值轨迹变化

图6.14（b）表明随着输出功率的增加，λ17，18振荡模态对应的阻尼比不断增大。且在输出功率小于0.24 p.u.时，对应的阻尼比为负值，系统处于失稳状态。优化PI参数在输出功率接近额定功率时对机网相互作用有较好的抑制作用，随着输出功率的降低，某些振荡模态对应的阻尼比不断减小甚至出现负值。也就是说，额定功率优化下的变流器控制参数有一定的适用范围，随着输出功率的下降对机网相互作用的抑制越来越弱甚至出现失稳的现象。因此，有必要对0.1～1 p.u.全输出功率下的变流器控制参数进行优化，从而得到全输出功率下变流器控制参数的选取。

通过相同的方法，对输出功率从0.1 p.u.到1.0 p.u.变化时，最优PI参数的改变进行记录，如表6.4所示。

表6.4　双馈风电机组变流器PI参数最佳区域随输出功率的变化

在风力发电系统输出功率变化的过程中，各个变流器控制参数的最佳运行范围如图6.15所示。其中，控制参数Kp4、Kp5、Kp6和Kp7基本保持不变，Kp1和Kp3变化范围较小，而Ki0、Kp0和Ki5发生了显著的变化。

图6.15　各控制参数最佳运行范围随输出功率的变化趋势