风电场分布式调相器优化策略

以下研究大规模多个风电场并网系统中，当存在多个节点供调相机接入时，调相机的配置优化策略。

1.实际风电场阻抗模型分析

以某地区实际电网为背景建立图5.29所示的风电并网系统。3个风电场均包含型号和工况相同的1.5 MW直驱风电机组。风电场中的风电机组经过机端升压变压器（0.69 kV/35 kV）升压汇集到35 kV风场出口母线。三个风电场输出的电能经过35 kV/220 kV变压器升压后，分别通过109 km和134 km的长距离输电线路汇集到母线D，再通过220 kV的双回输电线路（56.6 km）以及220 kV/750 kV升压变接入输电网。这里将实际系统750 kV侧（包含火电厂和直流输电）等值为交流电压源。根据实际风场检测到的持续次同步振荡，风场等值模型运行状态选取典型运行工况，即三个直驱风电场共有700台PMSG并网运行。

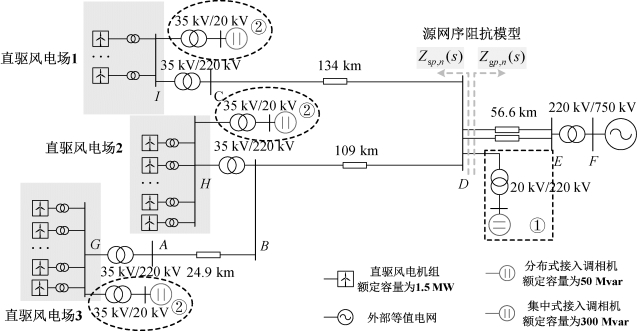
图5.29　多个直驱风电场连接弱交流电网

根据该地区运行数据的统计结果，低风速条件下，系统发生SSO的概率较大，因此设定所有风电机组运行出力水平为5%。在该运行工况下，母线A、B、C、D处的短路比分别为2.42、1.42、7.25、5.95。由此可以看出，直驱风电场2和3出口母线短路比较低，而直驱风电场1由于在一个长距离输电通道末端，且并网风机数量较少，其短路比相对较高。上述构造的直驱风电场并网系统等值模型及工况模拟了该地区直驱风机连接弱交流系统的场景。在多个直驱风电场连接弱交流系统中并联调相机前后的系统阻抗特性曲线如图5.30所示。

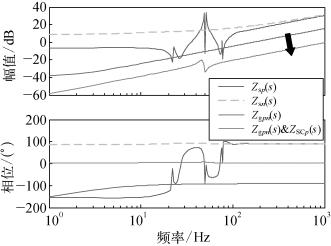
图5.30　调相机接入风场并网系统的序阻抗特性

观察系统源侧阻抗与网侧阻抗的关系可以发现，并入调相机前的网侧阻抗幅频曲线与源侧正序阻抗幅频曲线在次同步频段存在交点，有发生振荡的风险；并入调相机后的网侧阻抗幅值减小，网侧阻抗幅频曲线与源侧阻抗幅频曲线在次同步频段不再有交点。因此，从阻抗特性角度看，调相机增强了风场并网系统网侧交流系统强度，原理上源网之间不再有交互作用。该结果与单个直驱风电场连接弱交流系统分析结果一致。

2.集中式和分布式调相机抑制效果对比

由于新能源场站规模较大，地理位置分布较广，因此调相机存在着集中式接入和分布式接入两种接入方式。对此可以考虑调相机集中接入高电压等级和分散接入低电压等级两种配置方案。

在分布接入方式下，将3台额定容量为50 Mvar的调相机经20 kV/35 kV变压器接入直驱风电场各自的并网母线处，即母线G、H、I，如图5.29的②所示。图5.31是未加调相机、集中式接入1台调相机和分布式接入3台调相机的系统特征值对比。

从图5.31中可以看出，在系统中加入调相机能够减小主导模态的特征值实部，与图5.30中阻抗模型的结论得到了相互印证。与未接入调相机时系统特征值对比，集中式接入调相机和分布式接入调相机均能减小主导模态的特征值实部，降低系统发生次同步振荡风险。分布式调相机相对于集中式接入调相机对SSO的抑制效果更好。由于多风场通过长距离输电线路汇集，调相机分布式接入方式相对于集中式接入方式对风场出口母线处的短路容量支撑更大。同时，分布式调相机的总容量和造价也将低于集中式调相机的容量和造价。因此综合考虑振荡抑制效果和经济性，选用分布式接入方式更为合理。

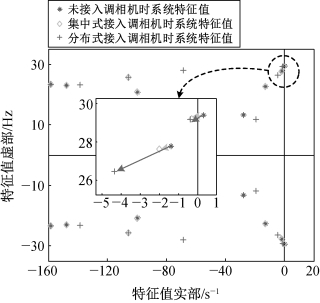
图5.31　不同方式接入调相机工况下系统　特征值对比图

3.分布式调相机配置优化策略

从分布式调相机SSO抑制结果对比来看，在风电并弱交流系统中，调相机的容量和配置位置是影响其振荡抑制性能的关键因素。从经济性角度看，不同容量调相机的配置成本存在差异，在进行调相机配置时，要考虑调相机的配置成本。分布式调相机配置优化的目的是以最少的成本发挥调相机对SSO最大抑制作用。将分布式调相机的配置问题抽象为优化问题，量化调相机对次同步振荡的抑制效果和配置经济性两个性能指标，将其纳入目标函数和约束条件，而后通过优化算法求解得到最优的调相机配置方案。

基于风机并网系统的小信号模型，采用振荡模态的特征值实部λSSO量化表示分布式调相机对系统SSO的抑制效果。振荡模态实部越小，调相机抑制效果越好，目标函数可设为

显然调相机成本越小，经济性越好。调相机的配置成本CSC包含安装调相机的固定成本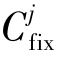（每台第j种容量调相机配置的固定成本）以及跟随容量变化的可变成本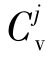（每Mvar无功容量调相机配置的可变成本），因此经济指标的目标函数可设为(www.xing528.com)

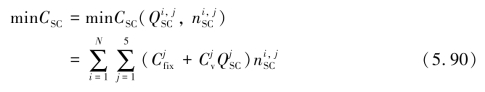
其中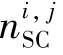，为第i条母线上配置的第j种调相机的台数，其无功输出额定值为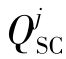，N是可供安装调相机的潜在备选母线总数。在本书研究中假设有5种额定无功容量不同的调相机，见表5.1。

表5.1　候选调相机容量

综合考虑调相机的抑制效果和经济成本，设置多目标函数，添加权重指标β。权重取值越小则越侧重抑制效果，反之则越侧重经济性。由于特征值和调相机配置成本量级相差较大，将经济性能指标归一化为C′SC，最终目标函数可描述如下：

直驱风机并网系统的振荡模态实部通过MATLAB的小信号模型的状态空间方程获得，将其作为优化模型的等式约束，如式（5.92）所示。

不等式约束为调相机台数限制以及风场并网点短路比要求，如式（5.93）和（5.94）所示。

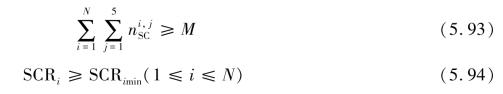
M是调相机的最大配置台数。本书研究系统中第i个母线短路比SCRi需维持在可接受的最小短路比SCRimin以上，避免系统处于弱交流工况。

由上述分析可知，调相机的振荡抑制效果与其容量和配置位置呈现非线性关系，且调相机的台数和配置位置是整数变量，因此该优化问题属于混合整数非线性规划问题，本书采用遗传算法进行求解。分布式调相机配置优化过程见图5.32。

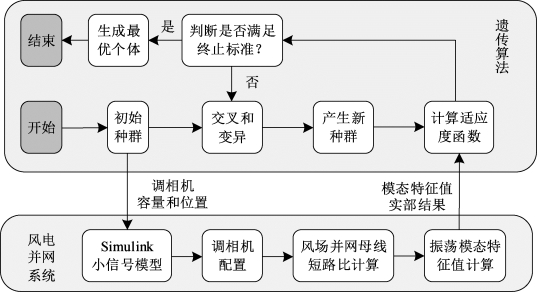
图5.32　调相机配置优化流程图

为了检验分布式调相机配置优化策略的效果，在PSCAD/EMTDC仿真平台搭建以该风电场为背景的多个直驱风电场连接弱交流系统。对调相机的位置和容量配置进行优化。遗传算法的参数设置如下：种群规模为160，最大的迭代次数为30，根据工程经验设定调相机的固定成本为1 000万元，可变成本为30万元/Mvar，最多可配置的调相机台数为5台，系统母线最小短路比SCRimin为3，权重β设置为0.1。调相机配置优化结果为在直驱风电场1、2、3出口母线处分别配置50 Mvar、200 Mvar、200 Mvar的调相机各1台，在三个风电场汇集母线处配置1台50 Mvar的调相机。图5.33显示了遗传算法中每代种群的平均适应度和最佳个体适应度的演变过程，可以看出，在30次迭代的时间里，最佳适应度的值（即目标函数的值）迅速向最优解进化。

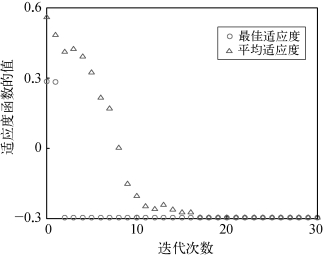
图5.33　最佳适应度和平均适应度迭代过程中的演化

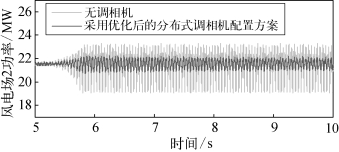
图5.34　调相机分布式接入方式的抑制结果

系统在优化后的分布式调相机配置方案下，系统振荡模态实部减小为－3.81，相较于未配置调相机（0.29）、集中式接入调相机（－0.30）和优化前分布式接入调相机配置方案（－0.45），模态实部大幅减小。在时域模型中应用优化后的调相机配置方案，仿真结果如图5.34所示。相较于未接入调相机的工况，优化后的分布式调相机配置方案将振荡幅值减小了76%。该方案下侧重于调相机对SSO的抑制效果（β＝0.1），分布式调相机配置成本为19 000万元，相较于集中式配置两台300 Mvar大容量调相机，成本下降5%。因此，基于遗传算法的分布式调相机位置和容量的优化策略实现了调相机对SSO抑制效果和配置成本的多目标优化和平衡。