变流器阻抗模型分析及优化

1.机侧变流器阻抗模型

机侧变流器（MSC）的阻抗模型建立过程中，由于MSC控制外环的时间常数较大，带宽低于100 Hz，所以，在针对高频谐振现象进行阻抗建模时，可以忽略MSC的外环控制回路。

MSC的控制策略中主要使用定子磁链定向模式，同时，由于DFIG定子电阻较小，推导控制策略时可以忽略定子电阻压降。此时，按照电动机惯例，定子磁链落后于定子电压90°电角度。

DFIG通过控制转子电流的方法实现对输出功率的控制。利用定子磁链关系式，可得到定子、转子电流关系，如式（5.27）。从式（5.27）可以看出，通过控制转子电流能够改变定子电流，也就可以进一步控制定子的输出功率。

式中，Ls＝Lls＋Lm为定子绕组自感；L′r＝L′1r＋Lm为定子绕组自感。

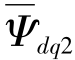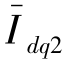要控制转子电流，就必须要得到转子电压方程。将转子磁链方程中的表示为与的函数：

当DFIG稳态运行时，电网电压不变，因而dq坐标系下的定子磁链复矢量也不变，不变，＝0。进一步可以将转子电压方程dq分量形式简化为

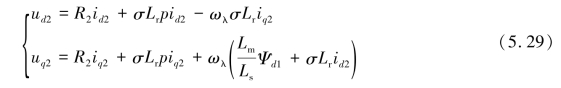
MSC控制器的输出为DFIG转子电压指令。只考虑MSC电流内环控制的MSC的输出电压指令表达式为

稳态下，指令值等于实际值，进一步得到dq坐标系下的机侧变流器输出的转子电压复矢量表达式为：

可以进一步推导出转子电压的空间矢量的表达式为

将上式经过整理后，可以将正序下的机侧变流器等效为由电压源和机侧变流器等效阻抗Zrsc串联组成的电路，其中，Zrsc＝Gr（s－jω1）－jKr。机侧变流器阻抗模型图如图5.8。

图5.8　机侧变流器阻抗模型

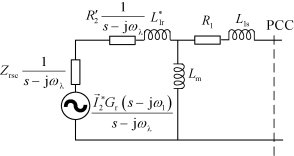
图5.9　机侧变流器与DFIG电机部分的阻抗模型

根据前文推导的感应电机的阻抗模型以及机侧变流器阻抗模型，可以得到机侧变流器连接感应电机转子侧的阻抗模型，如图5.9所示。

将电压源置零，可以得到PCC点处MSC和DFIG电机的阻抗模型。表达式如下：

(www.xing528.com)

式中，ZLM＝sLm为一定转子绕组之间的等效互感阻抗。

2.网侧变流器阻抗模型

网侧变流器（GSC）的工作原理是在控制过程中调节变换器的输出电压，控制输入GSC电流的幅值与相位，进而控制流入GSC的有功、无功功率。所以，GSC控制器输出上述两个分量也就是GSC的电压指令，经过坐标变换后输入到SPWM模块中。同样，网侧变流器中，为了保证设备的安全运行，也需要在控制器环节对电流进行有效控制，控制器一般采用比例积分（PI）形式。目前比较常见的GSC控制方法是令网侧变流器输出电压的d轴分量与电网电压相重合，电压q轴分量为零，即电网电压定向的矢量控制策略。该策略中网侧电压表达式如式（5.34）所示，网侧有功和无功功率的表达式如式（5.35）所示。

式中，u为电网相电压瞬时最大值（幅值）。

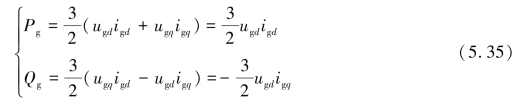
由式（5.35）可知，dq坐标系下，d轴分量和q轴分量互相正交，因而网侧的有功、无功功率可以实现解耦。也就确保有功功率仅与igd有关，与igq无关，无功功率与有功功率相反，与igd无关，仅与igq有关。

如果采用开环控制，电网参数会对网侧变流器的控制性能造成影响，为了减小这种困扰，对于电压和无功的控制回路采用闭环控制，控制器一般使用比例积分（PI）形式，最终输出电流有功、无功分量指令值，。

电流内环的闭环控制结构分为两部分，即控制器与被控对象。为了消除被控对象部分由ugd、ugq、ω1Lgigd、ω1Lgigq对前向通路造成的扰动，它们会一起作为前馈补偿项在电流内环的控制器中起作用。由此分析可知，电流内环比例积分控制器的输出ugd1、ugq1应如式（5.36）所示。

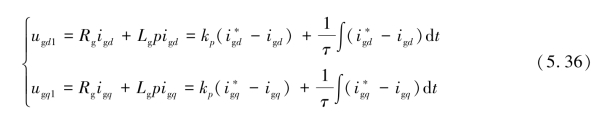
式中，kp为控制器比例系数；τ为控制器的积分时间常数。

接下来在式（5.36）所计算出的输出上叠加前馈补偿项ugd、ugq、ω1Lgigd、ω1Lgigq，得到GSC的控制结构的输出电压指令。表达式如下：

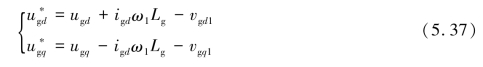
网侧变流器的控制系统分为电压外环控制和电流内环控制。但在高频谐振研究中，由于网侧变流器直流电压控制外环的时间常数较大，带宽低于100 Hz，在针对高频谐振现象进行阻抗建模时，就可以忽略网侧变流器的外环控制回路。可以得到只考虑电流内环控制的网侧变流器d、q轴电压和电流的表达式为

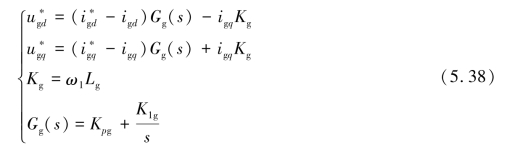
稳态下，指令值接近实际值，可以得到dq坐标系下网侧变流器的电压复矢量表达式为

式中，为dq坐标系下网侧变流器的参考电流复矢量；为dq坐标系下网侧变流器的实际电流复矢量。

可以推导出网侧电压的空间矢量的表达式如下：

式中，为abc坐标系下网侧变流器的参考电流空间矢量；为abc坐标系下网侧变流器的实际电流空间矢量。

经过整理后，可以将正序下的网侧变流器（GSC）等效为由电压源和网侧变流器等效阻抗Zgsc串联组成的电路，其中，Zgsc＝Gg（s－jω1）－jKg。网侧变流器阻抗模型如图5.10。

图5.10　网侧变流器阻抗模型