感应发电机阻抗模型优化方案

dq坐标系下的DFIG数学模型的电压方程如式（5.14）所示。

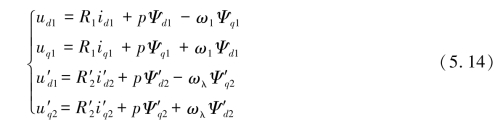
式中，ud1、uq1、u′d2、u′q2为定、转子电压的d、q轴分量；id1、iq1、i′d2、i′q2为定、转子电流的d、q轴分量；Ψd1、Ψq1、Ψ′d2、Ψ′q2为定、转子磁链的d、q轴分量；R1、R2为定子、转子绕组的等效电阻；ω1、ωr为电机同步转速、转子转速；ωλ为电机同步转速与转子转速之间相差的转差角速度，ωλ＝ω1－ωr。

式（5.14）其中定、转子磁链的d、q轴分量方程如式（5.15）所示。

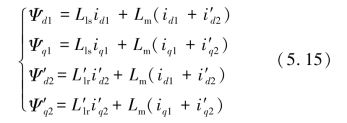
式中，Lls为dq坐标系下定子绕组的漏感；L′lr为dq坐标系下转子绕组的漏感；Lm为dq坐标系下，同一轴系上定转子绕组之间的等效互感，在感应发电机中，定子互感和转子互感相同，因而Lm＝1.5Lm1＝1.5Lm2，其中Lm1、Lm2分别是定、转子互感。

由电压和磁链方程可以得到感应电机等效电路如图5.6所示。

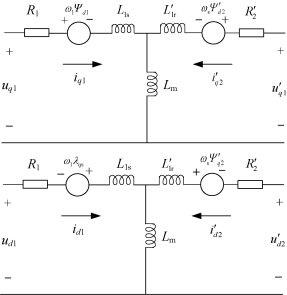
图5.6　dq坐标系下的感应电机等效电路

为建立abc坐标系下感应发电机阻抗模型，需要得到定子电压与定子电流和转子电压之间的表达式。在接下来的电机分析中，基于Lyon在电机分析中所使用的瞬态向量方法，dq轴系的方程将使用复数量表示，其中上箭头表示瞬态向量，因而复数量也被称作复数矢量，接下来将使用复数矢量称呼，它们与abc坐标系下的空间矢量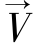的表达式为：

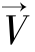式中，分别为感应电机的三相电压。当空间矢量逆时针旋转的时候为正值，而顺时针旋转的时候对应是负值。

利用上述所定义的矢量，将式（5.14）经过拉氏变换后，并代入式（5.15）所示的磁链方程，可以得到式（5.17）所示的转子电压复矢量的表达式。

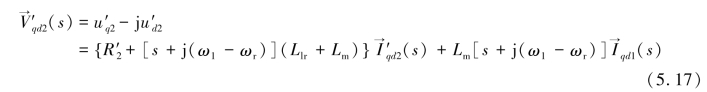
式中，为dq坐标系下的转子电流复矢量；为dq坐标系下的定子电流复矢量。

将式（5.17）进一步整理可以得到表示的表达式如下：(www.xing528.com)

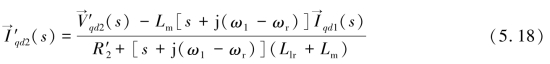
同理，利用前面所定义的矢量，将式（5.14）中的定子电压经过拉氏变换后，代入式（5.15）的定子磁链表达式，可以得到式（5.19）所示的定子电压复矢量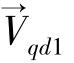的表达式。

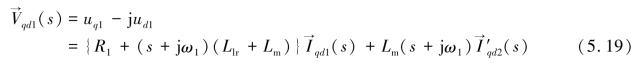
将式（5.18）代入式（5.19）中，得到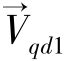表示的表达式如下：

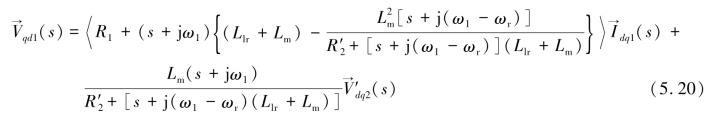
根据式（5.20），可以得到dq坐标系下的感应电机等效电路，但一般说来，电网补偿的RLC电路一般建立在abc坐标系下，因而，也需要将感应电机的等效电路进行变换。对式（5.16）所示的空间矢量表达式进行拉普拉斯变换后，电压空间矢量与dq坐标系下的定子电压复矢量的关系如下：

将式（5.21）代入式（5.20），可以得到abc坐标系下的定子电压空间矢量由定子电流空间矢量和转子电压空间矢量表示的关系式如下：

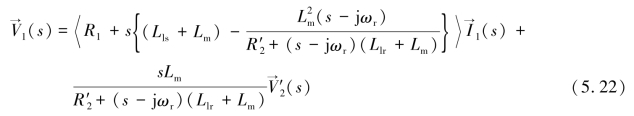
式中，感应电机的阻抗Z1表达式如式（5.23）所示。

但感应电机中，Lm≥R′2且Lm≥L′lr，因而阻抗表达式（5.23）可以进一步简化为式（5.24）。

根据上式，可以得到感应电机的阻抗模型如图5.7所示，但图中仅给出了感应电机内部的阻抗模型，对于DFIG系统，除了上述基本电机回路的阻抗外，还需要考虑机侧/网侧变流器的控制环节的阻抗建模和LCL滤波器的阻抗模型。

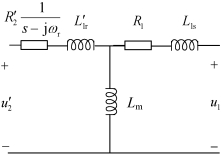
图5.7　abc坐标系下的感应　电机阻抗模型