阻抗分析法的原理详解

1.奈奎斯特稳定判据

基于阻抗的稳定性分析是将所研究的系统划分为源侧和负载侧两个子系统。源侧子系统的模型是由理想电压源（Vs）与输出阻抗（Zs）串联而成的戴维宁等效电路构成的，负载侧子系统由其输入阻抗（Zl）建模，如图5.1所示。

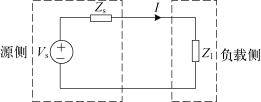
图5.1　带负载的电压源系统的小信号等效电路

由于几乎所有的电力电子电路都是非线性的，这种线性表示法只对小信号分析有效。

在假定的小信号模型下，从源侧流向负载侧的电流I为

可进一步转化为以下形式：

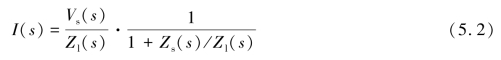
对于系统稳定性分析，假设源电压在空载时是稳定的，负载电流在由理想电源供电时是稳定的。在这种情况下，Vs（s）和1／Zl（s）都是稳定的，因此电流的稳定性就取决于式（5.2）右边第二项的稳定性。

(www.xing528.com)

基于阻抗的稳定性判据为：H（s）类似于负反馈控制系统的闭环传递函数，其中正向增益为1，反馈增益为Zs（s）/Zl（s），即源侧输出阻抗与负载侧输入阻抗之比。根据线性控制理论，当且仅当Zs（s）/Zl（s）满足奈奎斯特稳定性准则时，H（s）是稳定的。上述稳定性判据是基于电源子系统是电压源性质以及空载时电源电压能够保持稳定的基础上建立的，对于并网逆变器系统，其输出电压是由电网电压控制的，并网逆变器正常工作时是对入网电流进行控制的，表现为电流源性质，因此上述稳定性判据不能直接运用于并网逆变器系统。

对于电源子系统是电流源性质的系统稳定性判据同样是基于小信号等效电路的，如图5.2所示，并网逆变器即为其电源子系统，可以等效为电流源Ic与其输出阻抗Z0的并联形式，电网电压即为其负载子系统，可以将其等效为理想电压源Vg与输出阻抗Zg的串联形式。

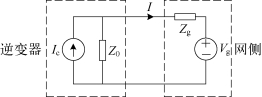
图5.2　并网逆变器系统小信号　等效电路

由图5.2可以计算出流进电网的电流I表达式为

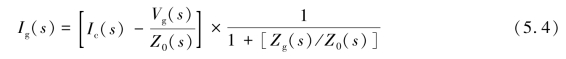
同样的，类似于前述电压源系统的稳定性分析电流源系统应用于稳定性分析时有如下前提条件，即当电网阻抗Zg为零时，进网电流I是稳定的，当没有并网逆变器时，电网电压Vg是稳定的。这种情况下，式（5.4）的稳定性主要取决于右边的第二项，该表达式同样类似于一个负反馈系统，它的前向通道增益是1，负反馈通道增益是Zg（s）/Z0（s），依据线性控制理论，只有当Zg（s）/Z0（s）满足奈氏判据时，系统能够稳定运行。上述判断是建立在电网稳定工作的假设下，如果电网运行不稳定，逆变器也无法稳定运行。

奈奎斯特稳定判据能够很好地判定系统的绝对稳定性（稳定或不稳定），并通过增益裕量和相位裕量两种度量来衡量系统的相对稳定性，因此在工程中获得广泛应用。

2.伯德图稳定判据

基于风电机组阻抗和电网阻抗频率特性曲线的伯德图稳定判据与奈奎斯特稳定判据的基本原理相似。通过解析法或者实测法获得风电机组和电网的阻抗－频率伯德图，通过分析风电机组阻抗幅频曲线与电网阻抗幅频曲线交点频率对应的二者相位差Δφ判断系统稳定性，若Δφ＜180°，系统稳定，反之，系统不稳定。伯德图判据不仅能够定性地判断系统稳定性，还能通过阻抗－相频曲线找出系统可能发生的振荡区域，这也是伯德图判据相较于奈奎斯特判据的优势所在。