忽略实际风电场电气连接,简化多机系统的小扰动模型如图4.12所示,假设所有风电机组都直接连接至公共连接点,经由变压器和输电线路接至无穷大系统,所有风机的参数、电气连接和阻尼特性相同。
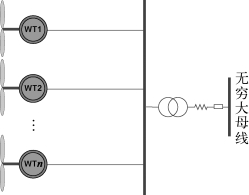
图4.12 简化多机系统小扰动模型
该系统的状态空间方程可以合并为
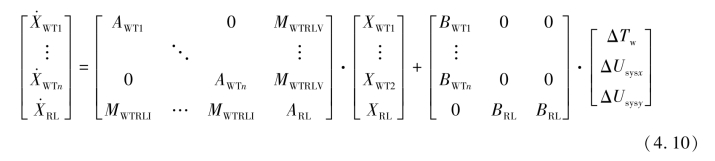
式中,MWTRLI反映风机与输电线路之间电流的连接关系,MWTRLV反映风机与输电线路之间电压的连接关系。
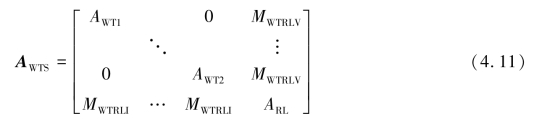
考虑如图4.13风电场,假设同类型风机具有完全一致的机械电气参数和运行状态。各风机单独运行,每台风机独立运行于一台变压器下,机端电压均为690 V,经变压器升压至10 kV,不同风电机组并联后再经由变压器升压至220 kV无穷大电源。考虑风机的最优布置,基于目前现场实际,风机的最小横向间距范围是2D~5D,最小纵向间距范围是5D~12D,假设我们风机叶片直径为50 m,可设置风机横向间距为100 m,风机纵向间距为300 m,该参数将在风机连接电缆参数中反映。
 (https://www.xing528.com)
(https://www.xing528.com)
图4.13 示例的风电场并网发电系统
图4.13的风电场由24台双馈风电机组组成,根据第3.1.1节表3.1系统参数,在Matlab/Simulink中搭建24台2 MW,0.69 kV双馈风电场小信号模型,系统状态矩阵A的特征值除零模态外,表4.4列出了系统的各个振荡模态,以及相应的振荡频率与阻尼比。由表4.4可知,除去零模态,上述双馈风电场共有8种振荡模态,观察相关因子表,可知该双馈风电场共有四种振荡模态,分别为14.576 5 Hz(1个),14.576 4 Hz(23个),2.820 4 Hz(1个),2.885 7 Hz(23个)。与第2章中双馈风机单机小扰动模型的仿真结果比较,可以看出原单机系统中与低速轴机械旋转角和角速度相关的振荡模态(14.576 4 Hz)在24机风电场中呈现为14.576 4 Hz和14.576 5 Hz,振荡频率基本不变。对比分析单机系统和风电场中该模态的参与因子,与低速轴状态变量相关的参与度从0.471 2变为0.018,相当于原单机模态的参与度平均到24台风电机组中,即各风机低速轴状态变量对该模态的参与度总和不变,同时观察两者阻尼比发现阻尼比基本不变。说明双馈风电场中由低速轴参数主导的振荡模态在风电机组间互作用较小。
另外,单机系统中与发电机转子机械旋转角和角速度相关的轴系扭振频率为2.885 3 Hz,在24机风电场中分别为2.820 4 Hz和2.885 7 Hz,其中频率为2.885 7 Hz的23个振荡频率与原单机系统接近,另一频率则相对变小,即风电机组间存在扭振传递相互作用。对比分析单机系统和风电场中与该模态相关的状态变量的参与度,可以看出发电机转子机械旋转角和角速度的参与度从0.028 3变成0.001 1,类似于低速轴参数主导的扭振模态,发电机转子机械旋转角和角速度对该模态的参与度总和基本不变。观察两者阻尼比,可看出原单机中该模态阻尼比从0.026 3变为24机风电场中的0.001 4和0.026 2,即频率变化较大的模态阻尼比也相应减小,风电机组在该振荡频率下更易发生机网作用。
表4.4 系统特征根分析

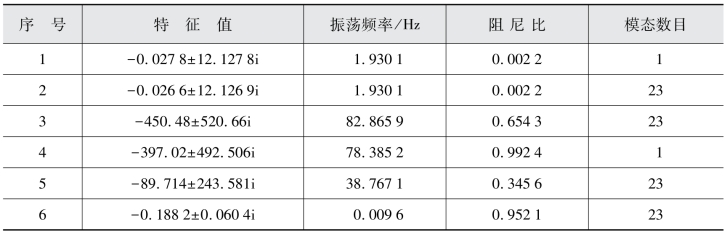
将图4.13风电场改为由24台永磁直驱风电机组组成,系统状态矩阵A的特征值零模态外,表4.5列出了系统的6个振荡模态,以及相应的振荡频率与阻尼比。具体分析同上,在此不再赘述。
表4.5 系统特征根分析
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




