永磁直驱风机发电系统网侧互动仿真验证

1.基于不可控整流升压电路的变流器永磁直驱风电机组的物理模型验证

为了进一步验证上述小信号模型中各个振荡模态的振荡频率，在MATLAB/Simulink中搭建2 MW基于不可控整流升压电路的变流器永磁直驱风电机组的时域模型，通过输电线路连接至无穷大电网。采用电压波动、功率波动等小扰动方式激发振荡，使用Simulink的FFT分析工具，结合表3.15给出的相关因子，在相应的相关变量上进行观测，可以发现与上述分析对应的全部机网相互作用模态。

由于特征值λ5，6对应的电气谐振模态由电机定子d轴磁链和q轴磁链主导，是系统的同步频率；λ12，13对应的振荡频率极低，不作为本书的研究重点，仅对次同步控制相互作用和次同步振荡进行仿真。

（1）次同步控制相互作用

上述小信号模型分析表明，λ1，2和λ3，4对应的振荡模态与输电线路电流和串补电容的端电压有很强的相关性，同时变流器直流侧电容的电压也对其起主导作用，对输电线路流过的电流进行频谱分析，得到其对应频谱特性如图3.15（a）和（b）所示。图3.15（a）表明，输电线路流过的电流中，在基频附近含有60 Hz和40 Hz左右的谐波成分，这与λ1，2对应的59.927 2 Hz、λ3，4对应的40.873 3 Hz的振荡频率相吻合。表3.11中的相关因子表明，λ7，8对应的振荡模态由直流电容两端的电压和网侧逆变器的控制系统主导，对直流电容的电压进行频谱分析，得到其频率特性如图3.15（b）所示。图3.15（b）表明，在直流电容的电压中除去直流分量外，主要还有1～2 Hz左右的谐波成分，这与模态λ7，8的振荡频率1.187 8 Hz相吻合。

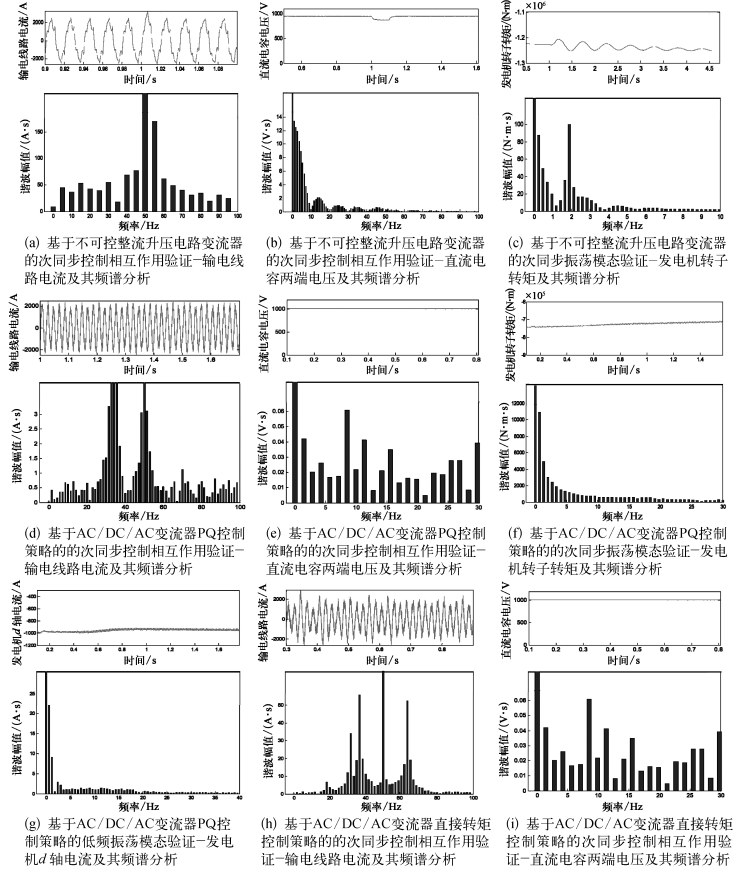
图3.15　永磁直驱风力发电机组机网相互作用的时域仿真

（2）次同步振荡

通过相关因子分析可以发现，λ9，10所对应的振荡模态由发电机的转子主导，因此，分析发电机的转子转矩，其对应的波形和频谱特性如图3.15（c）所示。发电机的转子转矩中除去直流分量外，主要还有1.95 Hz左右的谐波成分，这与模态λ9，10的振荡频率1.930 2 Hz相吻合。

2.基于AC/DC/AC变流器PQ解耦控制策略的永磁同步风电机组的物理模型验证

为了进一步验证上述小信号模型中各个振荡模态的振荡频率，在MATLAB/Simulink中搭建2 MW基于AC/DC/AC变流器PQ控制策略的永磁直驱风电机组的时域模型，通过输电线路连接至无穷大电网。采用电压波动、功率波动等小扰动方式激发振荡，使用Simulink的FFT分析工具，结合表3.13给出的相关因子，在相应的相关变量上进行观测，可以发现与上述分析对应的全部机网相互作用模态。

（1）次同步控制相互作用

上述小信号模型分析表明，λ1，2和λ3，4对应的振荡模态与输电线路电流和串补电容的端电压有很强的相关性，同时变流器直流侧电容的电压也对其起主导作用，对输电线路流过的电流进行频谱分析，得到其对应频谱特性如图3.15（d）所示。输电线路流过的电流中，主要含有70 Hz和38 Hz左右的谐波成分，这与λ1，2对应的71.454 0 Hz、λ3，4对应的38.228 4 Hz的振荡频率相吻合。(www.xing528.com)

表3.13中的相关因子表明，λ5，6对应的振荡模态由直流电容两端的电压和网侧逆变器的控制系统主导，对直流电容的电压进行频谱分析，得到其频率特性如图3.15（e）所示，在直流电容的电压中除去直流分量外，主要还有8 Hz左右的谐波成分，这与模态λ5，6的振荡频率7.565 7 Hz相吻合。

（2）次同步振荡

通过相关因子分析可以发现，λ7，8所对应的振荡模态由发电机的转子主导，因此，分析发电机的转子转矩，其对应的波形和频谱特性如图3.15（f）所示。发电机的转子转矩中除去直流分量外，主要还有1.9 Hz左右的谐波成分，这与模态λ9，10的振荡频率1.870 3 Hz相吻合。

（3）低频振荡

通过相关因子分析可以发现，λ14，15所对应的振荡模态由d轴磁链和机侧整流器的控制系统主导，而发电机的d轴电流决定了d轴磁链，因此，分析发电机的d轴电流，其对应的波形和频谱特性如图3.15（g）所示。发电机的d轴电流中除去直流分量外，主要还有0.2 Hz左右的谐波成分，这与模态λ14，15的振荡频率0.134 9 Hz相吻合。

3.基于AC/DC/AC变流器直接转矩控制的永磁直驱风电机组的物理模型验证

采用直接转矩控制的永磁直驱风力发电机组在Matlab中所搭建的时域模型，由于λ15，16所对应的振荡频率极低，对系统的影响可以忽略。

（1）次同步控制相互作用

上述小信号模型分析表明，λ1，2和λ3，4对应的振荡模态与输电线路电流和串补电容的端电压有很强的相关性，同时变流器直流侧电容的电压也对其起主导作用，对输电线路流过的电流进行频谱分析，得到其对应频谱特性如图3.15（h）所示。输电线路流过的电流中，除基波外，主要含有67 Hz和38 Hz左右的谐波成分，这与λ1，2对应的68.634 5 Hz、λ3，4对应的38.332 0 Hz的振荡频率相吻合。同时注意到，该输出电流中还含有30 Hz左右的谐波成分。

表3.15中的相关因子表明，λ5，6对应的振荡模态由直流电容两端的电压和网侧逆变器的控制系统主导，对直流电容的电压进行频谱分析，得到其频率特性如图3.15（i）所示。在直流电容的电压中除去直流分量外，主要还有8 Hz左右的谐波成分，这与模态λ5，6的振荡频率7.565 2 Hz相吻合。

（2）次同步振荡

通过相关因子分析可以发现，λ7，8所对应的振荡模态由发电机的转子主导，因此，分析发电机的转子转矩，其对应的波形和频谱特性如图3.15（j）所示。发电机的转子转矩中除去直流分量外，主要还有1.9 Hz左右的谐波成分，这与模态λ7，8的振荡频率1.870 3 Hz相吻合。

（3）低频振荡

通过相关因子分析可以发现，λ10，11所对应的振荡模态由d轴磁链和机侧整流器的控制系统主导，而发电机的d轴电流决定了d轴磁链，因此，分析发电机的d轴电流，其对应的波形和频谱特性如图3.15（k）所示。发电机的d轴电流中除去直流分量外，主要还有0.5 Hz左右的谐波成分，这与模态λ10，11的振荡频率0.365 6 Hz相吻合。