【摘要】：表3.7双馈风电机组连接至无穷大电网的小信号模型特征值表3.7列出的所有27个特征值中：有9对共轭的情况出现，即产生9种振荡模态；其余9个特征值虚部均为零，表现为非振荡模态。表3.8双馈风电机组各系统状态变量在各个振荡模式中的相关因子续表
该双馈风电机组连接至电网的小信号模型共有27个状态变量，分别是
式（3.20）中大部分状态变量的符号同表3.8中的定义一致，Δigx和Δigy是双馈风机变频器电网侧的电流状态变量。Δupc，x和Δupc，y虽然和表3.8中定义相同，但是在双馈风电机组中，可以不需要并联补偿电容进行无功补偿，此处的并联电容为电容值极小的对地电容，可以认为是集中参数线路的一部分，在此处的作用是用来在方程中转化电流和电压状态变量，便于前后元件模型连接，当然，该对地电容的容抗值极大，故电容电流极小。
在输电线路串补度为0.4时，通过Matlab/Simulink对上述小信号模型进行特征值分析，得到系统的特征根，系统所有的模态如表3.7所示。
表3.7 双馈风电机组连接至无穷大电网的小信号模型特征值
(www.xing528.com)
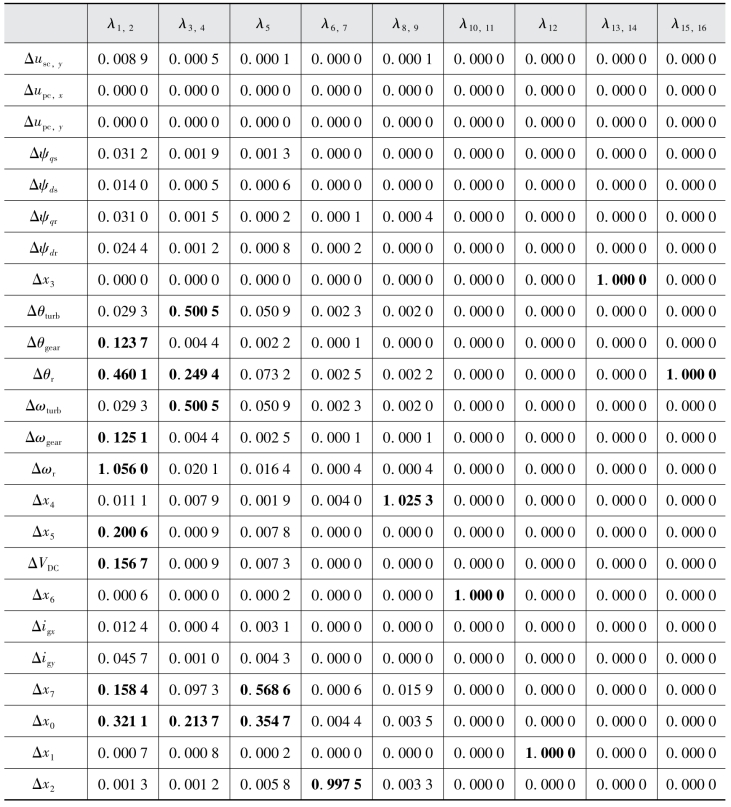
表3.7列出的所有27个特征值中：有9对共轭的情况出现，即产生9种振荡模态；其余9个特征值虚部均为零，表现为非振荡模态。为了确定各个振荡模式与哪些状态变量有关，在Matlab中进一步计算各个状态变量关于各个特征值的相关因子，结果如表3.8所示。
表3.8 双馈风电机组各系统状态变量在各个振荡模式中的相关因子
续 表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
