【摘要】：对于非线性系统，当其只在x0的一个领域内运动时，可将其用一阶线性系统近似代替。当A的全部特征根中至少有一个特征根的实部为正值时，线性化后的系统是不稳定的，且原来的非线性系统小范围不稳定。
电力系统小干扰稳定性研究涉及各种各样的动态元件，实质上是一个高维度、强耦合、非线性的复杂动态系统，可用非线性方程组（2.1）表示：
式中，x＝［x1，x2，…，xn］T。
对于非线性系统，当其只在x0的一个领域内运动时，可将其用一阶线性系统近似代替。设对应于x0的状态方程描述为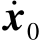
＝F（x0，u0，t）。将状态方程在（x0，u0）的领域内进行一阶Taylor展开，忽略无穷小量，得线性化后的系统微分方程是
式中，Δx＝x－x0；Δu＝u－u0；A为非线性系统在x0处的系数矩阵，B为非线性系统在u0处的系数矩阵，即
对于非线性系统方程组（2.1）在x0邻域内的小范围稳定性是由该系统线性化后特征方程（2.2）的根，即雅可比矩阵A的特征值决定的：(www.xing528.com)
（1）当A的全部特征根的实部都为负值时，线性化后的系统是渐进稳定的，且原来的非线性系统小范围渐进稳定。
（2）当A的全部特征根中至少有一个特征根的实部为正值时，线性化后的系统是不稳定的，且原来的非线性系统小范围不稳定。
（3）当A的全部特征根中至少有一个特征根的实部为零，且其他特征根的实部都为负值时，线性化后的系统处于临界状态，不能用线性化后的系统得出原非线性系统是否小范围稳定的结论。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
