工期和资源优化策略

完成一项工程所需的资源量基本是不变的，不可能通过资源优化得以减少，资源优化的目的是通过改变工作的开始和完成时间，使资源按照时间的分布满足优化目标要求。资源优化通常分为“资源有限、工期最短”优化和“工期固定、资源均衡”的优化。

1）“资源有限、工期最短”

为简化这种优化问题，假设所有工作需要的都是同样的资源，在项目建设过程中，当某种资源受到限制时，资源计划必须满足其限量进行安排。“资源有限、工期最短”的优化是利用工作时差，改变某些工作的最早开始时间，以满足资源限量的要求。

基本术语：

①资源强度：指工作i—j对第K种资源的单位时间需要的强度。

②资源需要量：，为项目t时段对第K种资源总的需要量。

③资源限量：Ra为每单位时间提供固定的资源强度。

优化步骤：

①绘制早时标网络及资源动态曲线。

②逐时段检查，当出现Rt＞Ra时，作为调整时段。

③对调整时段平行工作重新安排（改变某些工作的开始时间），计算各方案工期延长值：

ΔTm，n＝EFm＋Dn－LFn＝EFm－（LFn－Dn）＝EFm－LSn

式中　ΔTm，n——将工作n安排在工作m之后进行时网络计划的延长值。

④在有资源冲突的时段中，找出所有的并行工作，并求出它们的最早完成时间和最晚开始时间，为求最小的（即延长工期最短的）ΔTm，n，最佳方案的公式可表示为：

ΔTm，n＝minEFm－maxLSn

因此，只要找出最小的最早完成时间值和最大的最晚开始时间值所属的工作即可。

注意：若某工作的EF是最小值并且LS为并行工作的最大值，则找次级的与之比较即可。

⑤重复以上步骤，直到满足要求为止。

【例题7.12】　某工程项目的双代号时标网络进度计划（单位：天）如图7.29所示，箭线之上的数是工作的资源强度。假设每天可供资源为20个单位，试确定其在满足资源限制条件下的最短工期。

【解】　（1）计算并绘制该工程网络计划每个单位时间的资源需要量，资源需要量动态曲线如图7.30所示。

（2）从开始日期起，逐个检查每个时段资源是否满足要求，本题第4、5、6天资源超限，需进行调整。第4天的并行工作有：A、D、E。(www.xing528.com)

由计算得知：EFA＝4，EFD＝6，EFE＝7，LSA＝2，LSD＝4，LSE＝3

minEFm＝4，maxLSn＝4，m为工作A，n为工作D。综上可知工作A→D的工期延长值最小，调整方案为：将工作D移到工作A之后。调整以后的时标网络计划以及资源需要量曲线如图7.31所示。

（3）由图7.31可知第5、6、7周资源超限，并行工作为：G、D、E。

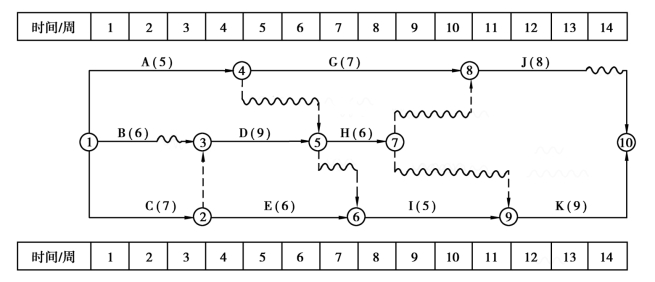
图7.29　某工作早时标网络计划图

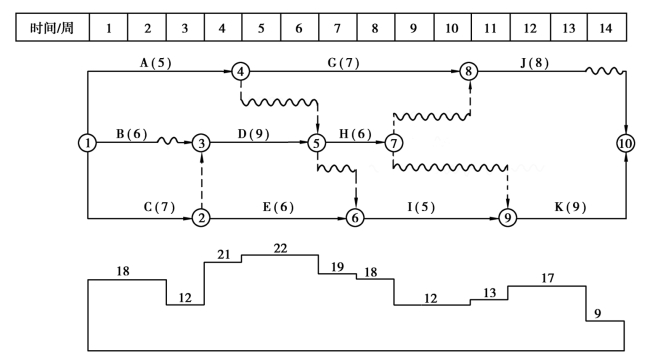
图7.30　初始时标网络计划以及资源需要量曲线

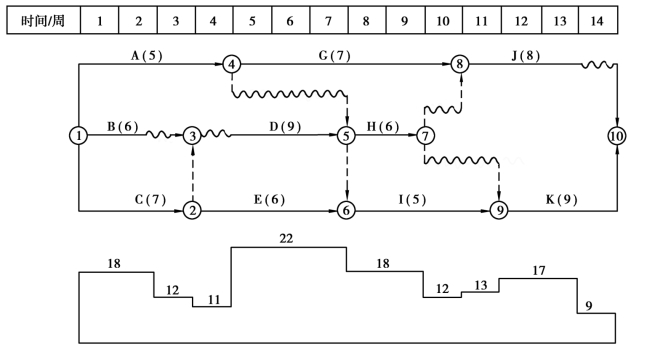
图7.31　第一次调整后时标网络计划以及资源需要量曲线

由计算得知：EFG＝10，EFD＝7，EFE＝7，LSG＝6，LSD＝4，LSE＝3

minEFm＝6，maxLSn＝6，m为工作D，n为工作G。综上可知工作D→G的工期延长值最小，调整方案为：将工作G移到工作D之后。调整后的时标网络计划以及资源需要量曲线如图7.32所示。

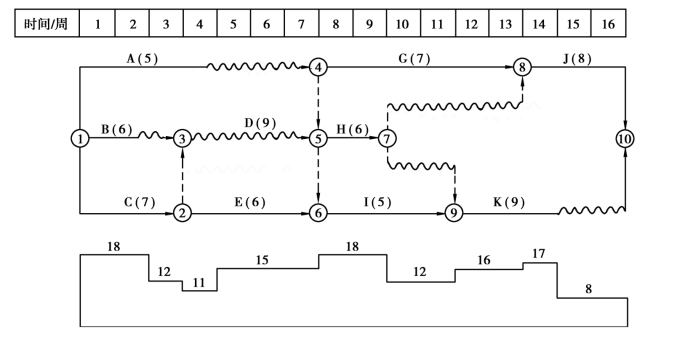
图7.32　第二次调整后时标网络计划以及资源需要量曲线

（4）由图7.32的资源需要量曲线可知第二次调整后满足资源限量小于20个单位的要求，因此最终优化结果如图7.32所示，最短工期为16周。

2）“工期固定、资源均衡”

工程项目建设过程是不均衡的生产过程，对资源种类、用量需求等常常会有大的变化。通过网络计划中非关键工作时差的利用对资源计划进行调整（削峰填谷），尽量减少资源需用量的波动，使资源连续而均衡分布。

衡量资源需用量的不均衡程度有3个指标：

①不均衡系数：K＝Rmax/Rm。

②极差值：ΔR＝Min（Rt－Rm）。

③均方差值：。