74LS161计数器电路详解

1.74LS161 计数器电路的设计

用74LS161 进行计数器电路设计有两种方法，即反馈清零法、反馈置数法。

注意：一片74LS161 设计的计数器电路最高模M=16，即计数器电路最高计数为十六进制计数器逻辑电路。

1）反馈清零法

反馈清零法是通过状态表11.3 中“清零”和“计数”两项功能（如表11.8 所示），完成小于十六进制计数器逻辑电路的设计。

表11.8　“反馈清零法”的状态表

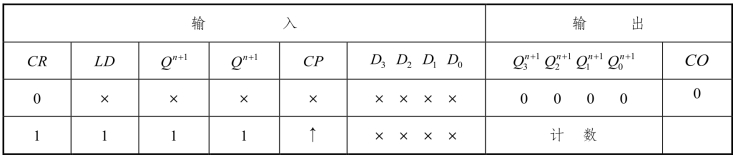
当设计的计数器为M 进制时，则利用CR 端清零信号使计数器输出状态Q 为0 状态。

【例11.6】 试用反馈清零法分别设计由74LS161 构成的“十二进制”和“八进制”计数器。分析：

（1）“十二进制”说明计数器的模M=12，即当时，向CR 端输入一个低电平清零信号，使由1100 转变成0000，其状态转换如图11.25（a）所示。

（2）“八进制”说明计数器的模M=8，即当时，向 CR 端输入一个低电平清零信号，使由1000 转变成0000，其状态转换如图11.25（b）所示。

（3）LD、CTP、CTT在“清零”时为无关项，但工作在“计数”状态下时必须接高电平信号，所以接高电平；D3D2D1D0没有输入电平高低要求，可以直接接地。

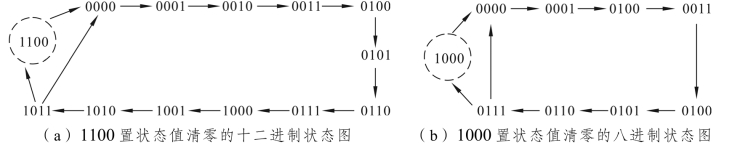
图11.25　“反馈清零法”状态转换图

解　十二进制计数器逻辑电路如图11.26（a）（c）所示；八进制计数器逻辑电路如图11.26（b）所示。

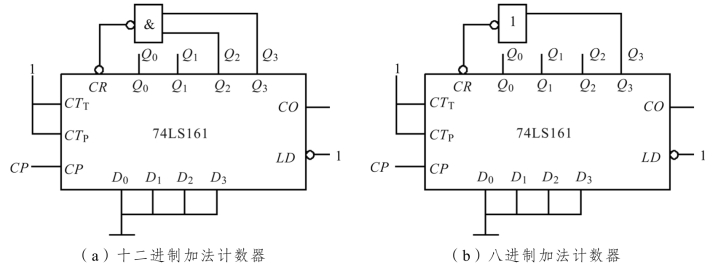
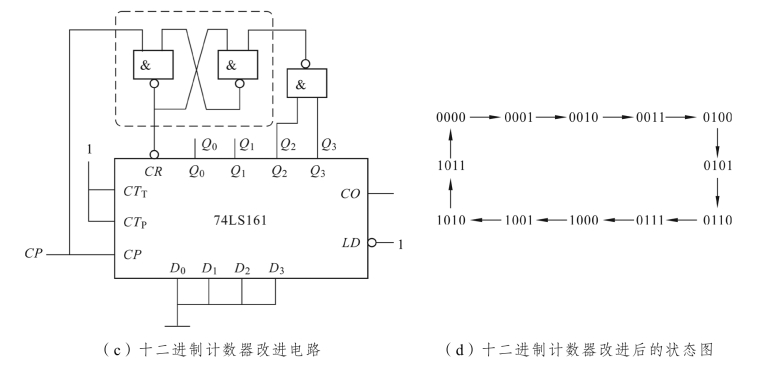
图11.26　“反馈清零法”构成74LS161 的十二进制加法计数器

结论：反馈清零法是用计数器模M 所对应的输出状态Q 产生清零信号，即CP 产生模M输出Q，Q 再反馈产生清零CR 信号，所以，计数器的清零采用的是异步方式。

注意：如果图11.26（a）（b）电路的“清零”时间太短，则电路不能可靠运行。因此，图11.26（c）为图11.26（a）的改进电路。即当CP 发出触发信号时，输出状态 Q3Q2Q1Q0=1100，则产生清零信号CR=0，输出状态为0000，这时只要CP=1，清零信号CR=0保持不变，提高电路“清零”的稳定性；当CP 脉冲信号由1 下降为0（即CP=0）时，CR=1，74LS161进入计数状态。改进后电路状态转换如图11.26（d）所示。

2）反馈置数法

反馈置数法是通过状态表11.3 中“置数”和“计数”两项功能（如表11.9 所示），完成小于十六进制计数器逻辑电路的设计。

表11.9　“反馈置数法”的状态表

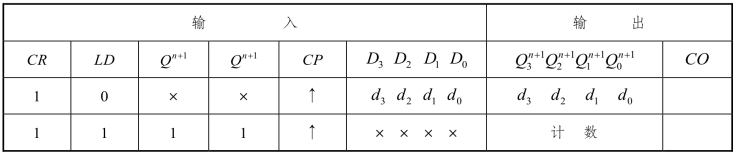
利用LD 的低电平信号置新态从而改变计数器的循环状态。

【例11.7】 试用反馈置数法设计由74LS161 构成的十二进制计数器。

分析：

（1）当LD=0时，在CP 脉冲信号作用下置为起始状态值。

（2）图11.28（a）反馈置为起始状态值（即置数为零），其状态转换如图11.27（a）所示；图11.28（b）反馈置为起始状态值（即置数为4），其状态转换如图11.27（b）所示。

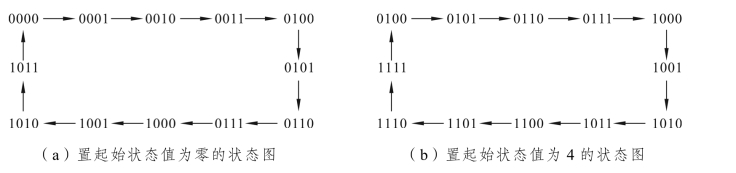
图11.27　“反馈置数法”置起始状态值的状态转换图

解　十二进制计数器逻辑电路如图11.28 所示。

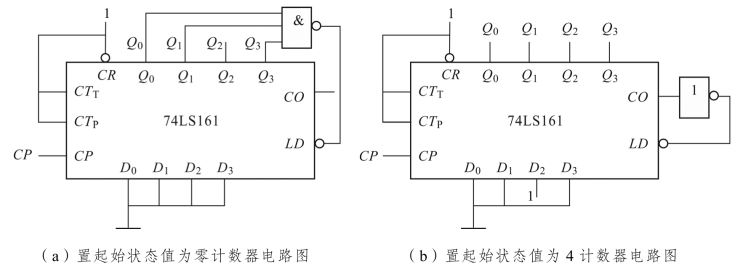
图11.28　“反馈置数法”构成74LS161 的十二进制加法计数器电路图

结论：用LD 置起始状态值是“反馈置数法”中的一种，还可以利用置状态值为1111 设计电路（即置状态值为15），例如：用状态为1010 置数1111，即十二进制计数器状态转换为0000～1010→1111。

3）74LS161 扩展功能的设计

一片74LS161 最高只能构成十六进制计数器，如要设计大于16 的计数器，就要用更多的74LS161 芯片组合完成。

【例11.8】 试用两片74LS161 组成256 进制加法计数器。

分析：

（1）高、低位计数器分配：256（即16 × 16=256）进制计数器的扩展电路有两种连接方式，如图11.29 所示，其中74LS161（1）为低位计数器，74LS161（2）为高位计数器。

（2）进位输出端CO：当输出状态在0000～1110 区间时，进位输出端CO=0，只有输出状态 Q3Q2Q1Q0=1111、CPT=1时，CO=1，即逻辑表达式CO=Q3Q2Q1Q0∙CPT。

（3）同步加法计数器设计：如图11.29（a）所示，由于低位进位输出端CO 接高位的状态控制端CTT高、CPP高，所以，当低位CO=1时，高位的CTT高=CPP高高=1，高位进入计数状态；当低位CO=0时，高位的CTT高=CPP高高=0，高位进入保持状态，如表11.10 所示。

表11.10　74LS161 的状态表(www.xing528.com)

（4）异步加法计数器设计：如图11.29（b）所示。利用低位进位输出端CO低由1 变换为0（下降沿脉冲）信号；作为高位计数器的CP 触发信号，即用非门将下降沿触发信号转换为上升沿CP 触发信号。

解　两片74LS161 组成16 × 16=256进制加法计数器，如图11.29 所示。

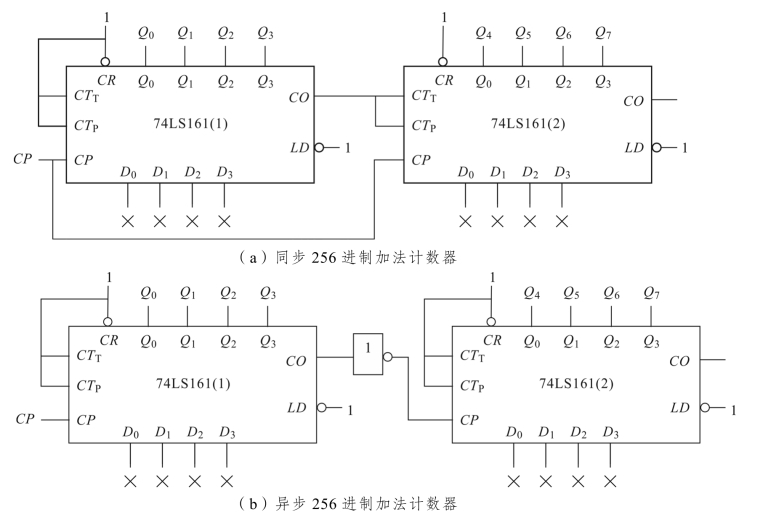
图11.29　两片74LS161 组成256 进制加法计数器电路图

结论：多片74LS161 的扩展应用时，有两种方式扩展连接电路，即同步方式、异步方式。同步加法计数器设计原理是：用低位的进位CO 信号控制高位的状态控制端CTT、CPP；异步加法计数器设计原理是：低位的进位CO 输出信号是高位CP 端的脉冲输入信号。

【例11.9】 试用74LS161 构成62 进制加法计数器。

分析：

（1）因为16 ﹤62 ﹤256，所以用两片74LS161 进行设计。

（2）第一步作扩展为256 进制计数器电路设计，即分别用了两种扩展方式设计。

（3）用“反馈置数法”构成62 进制加法计数器。

解　数学分解

即当74LS161（2）计数为0011、74LS161（1）计数为1101 时，向LD 端发出低电平置0 信号，如图11.30 所示。

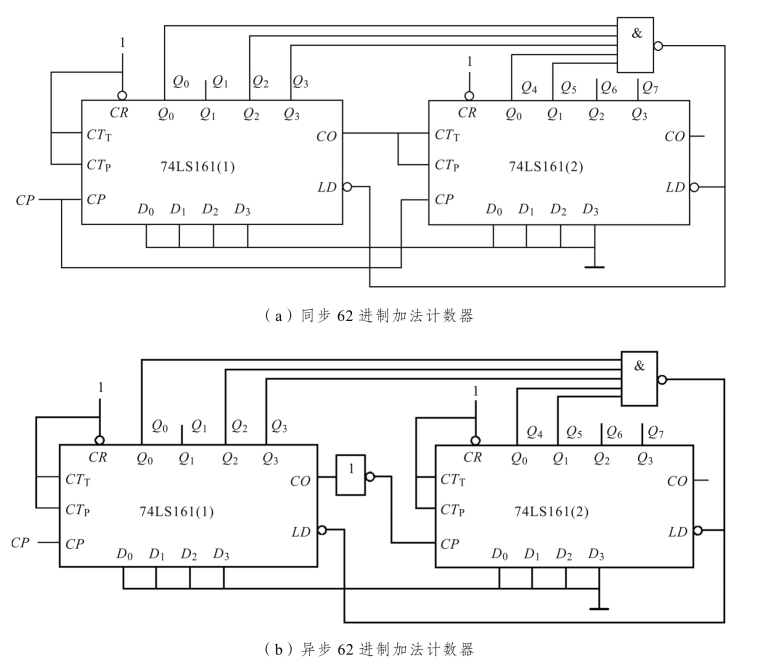
图11.30　62 进制加法计数器电路图

结论：注意高、低位置数信号的不同。算式62=16 × 3+14中的3 表示高位从0 开始计3个16，所以，高位置数信号是0011；算式62=16 × 3+14中的14 表示低位从0～13 计脉冲信号数14 个，所以，低位置数信号是1101。置数信号通过与非门转换为LD 的低电平输入信号。

如果要设计一个M（16﹤M﹤256）进制加法计数器，列式M=16× m1+m2（注：m2﹤16），则高位置数信号的状态值是 m1，低位置数信号的状态值是（m2-1），高、低置数信号通过与非门转换为置数控制端LD 的低电平输入信号。

2.74LS161 计数器电路的分析

电路的分析指的是对已知的74LS161 计数器电路图进行功能分析。

【例11.10】 试分析图11.31 所示电路是几进制计数器，画出状态转换图。

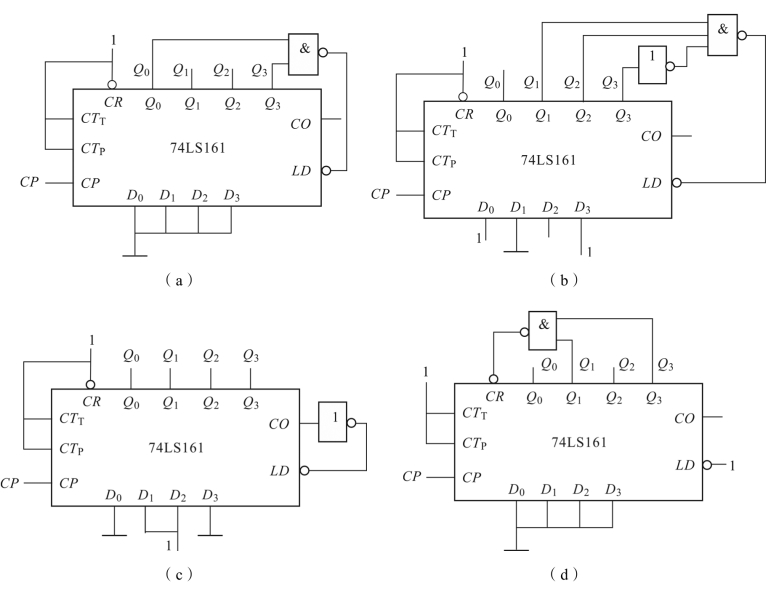
图11.31　例11.10 电路图

分析：

（1）图11.31（a）（b）（c）应用的是“反馈置数法”设计的计数器电路。图11.31（a）用输出状态1001 置 Q3Q2Q1Q0状态为0000，其状态转换如图11.32（a）所示；图11.31（b）用输出状态0110 置 Q3Q2Q1Q0状态为1101，其状态转换如图11.32（b）所示；图11.31（c）进位输出状态1111 置 Q3Q2Q1Q0状态为0110，其计数器状态转换如图11.32（c）所示。

（2）图11.31（d）应用的是“反馈清零法”设计的计数器电路，用输出状态1010 反馈清零 Q3Q2Q1Q0，其状态转换如图11.32（d）所示。

解　分析状态转换图11.32，可得图11.31 各电路为十进制计数器。

图11.32　例11.10 题的计数器状态转换图解

结论：一片74LS161 计数器电路分析步骤如图11.33 所示。

（1）反馈信号接CR 端为“反馈清零法”；反馈信号接LD 端为“反馈置数法”。

（2）“反馈清零法”：清零Q 值M 直接确定电路为M 进制计数器[如图11.31（d）所示]。

（3）“反馈置数法”：如果LD 端接入的是进位CO 输出信号[如图11.31（c）所示]，则电路为（16-N）进制计数器（注：N 表示D 端的数据值）；如果LD 端接入的是输出状态Q 信号[如图11.31（a）（b）所示]，则根据N 值推出计数器的进制，即N=0时为（M+1）进制计数器，N ≠0时为（17+M-N）进制计数器。

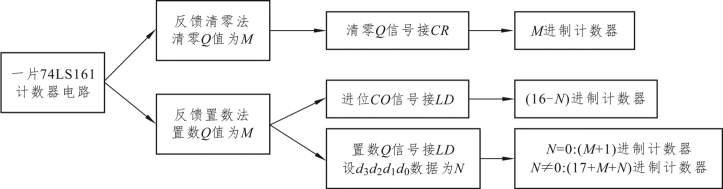
图11.33　一片74LS161 计数器电路分析示意图

【例11.11】 试分析图11.34 所示电路是几进制计数器。

分析：图11.34 是由两片74LS161 构成的同步加法计数器。74LS161（1）为低位计数器，其置位Q 值为14；74LS161（2）为高位计数器，其置位Q 值为6。

图11.34　例11.11 题电路图

解　计数器的进制为M=16 × 6+15=111，即是111 进制计数器电路图。

结论：两片74LS161 可扩展构成256 进制计数器。设低位计数器的置位Q 值为 m1，高位计数器的置位Q 值为m2，则电路的模M=16m2+m1+1。