实现多位二进制数相加的串行进位加法器电路

图10.30 中 Ai、Bi为两个1 位二进制数；Si为本位相加之和；Ci为向高位的进位；Ci-1为低位的进位。

加法器分为半加器和全加器两种，其加法运算原理如图10.30 所示。

二进制加法运算原则：0+0=0，0+1=1，1+1=10。

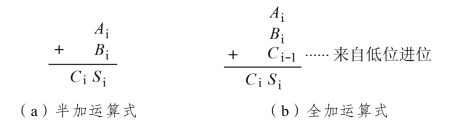
图10.30　加法运算式图

1.半加器

不考虑来自低位的进位将两个1 位二进制数相加，称为半加，实现半加运算[见图10.30（a）]功能的电路称为半加器。

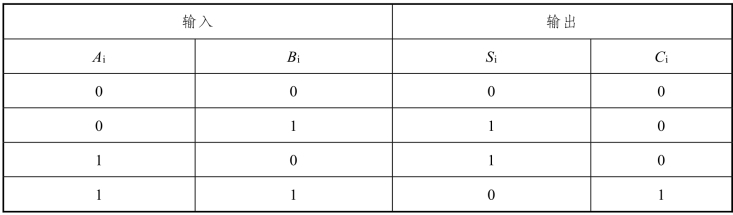
半加器示意图如图10.31（a）所示。根据二进制加法运算法则，半加器功能如表10.13所示。

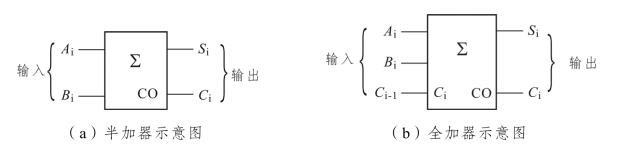
图10.31　加法器示意图

表10.13　半加器真值表

2.全加器(www.xing528.com)

设两个二进制数为A=1011、B=1001，则A 与B 相加为10100，其加法运算过程如图10.32所示。

可见，加法运算中，除了本位相加和向高位进位外，还要考虑低位来的进位。即两个1 位二进制数 Ai、Bi以及来自低位的进位数 Ci-1三者相加[见图10.30（b）]，称为全加，实现全加功能的电路称为全加器。

全加器示意图如图10.31（b）所示。其功能如表10.14所示。

图10.32　A+B 运算式示意图

表10.14　全加器真值表

【例10.10】 试用4 个全加器构成能实现A=A3A2A1A0、B=B3B2B1B0相加的串行进位加法器电路。

分析：“串行进位加法器电路”是指连接电路时，第一个全加器的进位输入 C0-1接地，其他全加器依次将低位全加器的进位输出接到高位全加器的进位输入，从而构成串行进位（或逐位进位）加法器电路。

解 A+B串行进位加法器电路如图10.33 所示。其中，输出数码 C3S3S2S1S0表示了二进制数 A3A2A1A0与 B3B2B1B0之和，即A+B=A3A2A1A0+B3B2B1B0=C3S3S2S1S0。

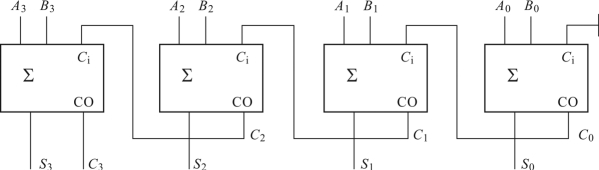
图10.33　4 位串行进位加法器电路图

结论：若干全加器级联构成多位全加器。这种串行进位连续方式的最大缺点是运算速度慢。