电路设计：比例运算、微分运算和积分运算

本节主要讨论运算电路中，输入电压与输出电压的关系式，即 uo=f（ui）或在分析运算电路过程中，主要涉及电路理论和运算放大器的知识点有：

电路理论方面：欧姆定律u=Ri、基尔霍夫定律（KCL、KVL）和电容元件的伏安特性

运算放大器方面：“虚断” ii≈0[式（8.2）]和“虚短”u-≈u+[式（8.3）]两个重要特性。

1.比例运算电路

1）反相比例运算电路

反相比例运算电路如图8.11（a）所示。根据式（8.2）可知流过电阻R2的电流为零，并且同相输入端u+通过电阻R2接“地”，得

图8.11　比例运算电路

所以由式（8.3）得

即反相输入端u-“虚地”。再根据KCL 得

因式（8.2）特性i ≈0，则

由图8.11（a）电路分析得

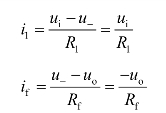
将上式代入式（8.7），得 uo=f（ui）关系式为

由式（8.8）得闭环电压放大倍数 Af为

式（8.8）表明，输出电压 uo与输入电压 ui是反相（式中负号表示uo与ui反相）比例运算关系，或者说反相放大关系。如果R1和Rf的阻值足够精确，而且运算放大器的电压放大倍数很高，就可以认为uo与ui间的关系只取决于Rf和R1的比值，与运算放大器本身的参数无关，这就保证了比例运算的精度和稳定性。

当图8.11（a）中电阻 R1=Rf时，式（8.8）、式（8.9）得

即图8.11（a）电路为反相器。

图8.11（a）中电阻R2称为平衡电阻。即：当ui=0时，为了保持运算放大器的输入端电路的对称性，要求由反相输入向左看去的等效电阻（R1//Rf）必须等于由同相输入端向左看去的等效电阻R2，电路如图8.12 所示，解得

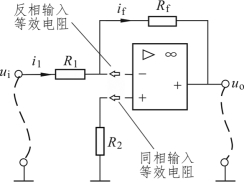
图8.12　平衡电阻分析电路图

2）同相比例运算电路

同相比例运算电路如图8.11（b）所示。由式（8.2）得流过电阻R2的电流为零，即

由式（8.3）得

分析电路图8.11（b）得

由式（8.7）（i1≈if）得

图8.13　电压跟随器电路

当图8.11（b）中电阻R1=∞，或Rf=R2=0 时，如图8.13 所示，由式（8.11）、式（8.12）得

图8.13 所示电路称为电压跟随器。

2.加法运算电路

1）反相加法运算电路(www.xing528.com)

反相加法运算电路如图8.14（a）所示。因u-≈u+=0，则

当图8.14（a）所示电路中的电阻R11=R12=R1时，由式（8.13）得

图8.14　加法运算电路

当图8.14（a）所示电路中的电阻R11=R12=Rf时，由式（8.13）得

由式（8.13）、式（8.14）和式（8.15）可见，加法运算电路也与运算放大器本身的参数无关，电阻器件的精度决定加法运算的精度和稳定性。

2）同相加法运算电路

同相加法运算电路如图8.14（b）所示。根据图8.14（c）计算图8.14（b）电路中的u+为

因u-≈u+，解图8.14（b）得

3、减法运算电路

差动运算放大电路在测量和控制系统中应用很广泛，它的两个输入端都有信号输入，其运算电路如图8.15 所示。

图8.15　减法运算放大电路

解得

当图8.15 电路中电阻R1＝R2和Rf＝R3时，由式（8.16）得

当R1＝RF时，式（8.17）得

式（8.18）说明，当电阻 R1=R2=R3=Rf时，可直接实现两输入电量 ui1、ui2的减法运算，即同相输入电量 ui2减去反相输入电量 ui1。

4.积分运算电路

积分运算电路如图8.16（a）所示。u+=0，根据运算放大器特性有u-≈u+=0，i=0，解图（a）得

由电容元件的伏安特性得

因u+=0，得

式（8.19）表明uo与ui的积分成正比例。

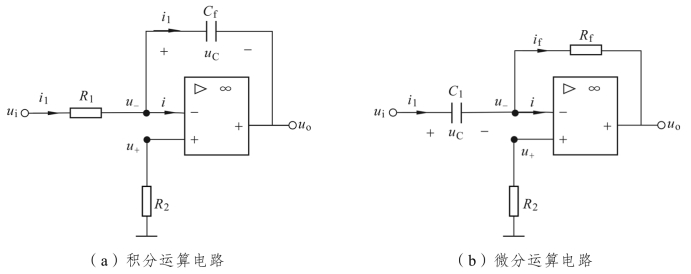
图8.16　积分和微分运算电路

5.微分运算电路

微分运算电路如图8.16（b）所示。根据u-≈u+=0得

由电容元件的伏安特性得

因i=0，由KCL 得

将式（8.20）代入上式，得

式（8.21）表明 uo与 ui对时间的一阶导数成比例。