二极管基本模型及电路分析

1.二极管正向特性模型

在分析二极管的应用电路时，可以根据不同的场合和使用条件，选择不同的模型来等效代替。本教材主要介绍理想模型和恒压降模型两种。如图6.5 所示。

图6.5　二极管的等效模型图

1）理想模型

二极管相当一个理想开关，正向导通，反向截止，如图6.5（a）所示。

当二极管D 外加正向电压u﹥0 V时，二极管D 为“正向导通”状态，二极管D 等效为“短路”；当二极管D 外加反向电压u 时，二极管D 为“反向截止”状态，二极管D 等效为“开路”。

此模型主要用于低频大信号电路之中，例如整流电路。

2）恒压降模型

当二极管D 外加正向电压u≥UD死区电压时，忽略正向动态电阻，二极管D 等效为“恒压源UD”；当u ﹤UD时，二极管D 等效为“开路”。如图6.5（b）所示；

此模型主要用于低频小信号电路。

2.二极管电路分析

正确判断出二极管的工作状态是分析二极管电路的关键，即：是导通状态，还是截止状态。

【例6.1】 在图6.6（a）所示的电路中，已知二极管正向偏置电压为0.7 V，电压源为 US1=5 V，US2=10 V，电阻 R1=R2=10 kΩ，R3=R4=5 kΩ，试判断二级管是导通还是截止，并求流过二级管的电流。

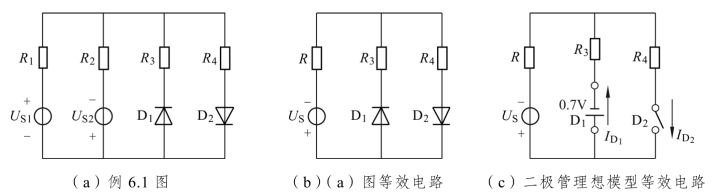
图6.6　例6.1图及电路分析图

分析：

（1）因二极管是非线性元件，所以不能用叠加定理进行分析计算，可以用戴维南定理或电源模型等效变换法，如图6.6（b）所示。

（2）根据二极管正向偏置电压为0.7 V，用恒压降模型等效替代二极管。如图6.6（c）所示。

解　由戴维南定理计算图（a）得图（b），其参数为

在图（b）中的电压源US作用下，二极管D1承受的是正向电压，即D1导通；D2承受是反向电压，即D2截止。其等效电路如图（c）所示，则流过二极管的电流分别为

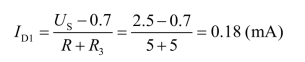(www.xing528.com)

结论：二极管是非线性元件，叠加定理不能用于非线性电路分析。

【例6.2】图6.7（a）电路中，已知二极管为理想元件，试判断二极管的工作状态，并求电压UAO。

图6.7　例6.2图及分析判断图

分析：因二极管由截止状态过度为导通状态时，要通过一个“死区”，所以，当若干个二极管同时处于正向偏置电压时，正向偏置电压较大的二极管优先导通；其他的二极管是否导通，须在优先导通二极管的条件下继续再做判断，以此类推。

解　设二极管正向偏置电压如图（b）所示，得

因UD1﹤UD2，所以，D2管优先导通。由图（c）解得

则D1管截止，电压UAO为

结论：二极管在“截止”与“导通”相互转换时，要经过一个“死区”。因此，在几个二极管同时处于正向偏置电压时，正向偏置电压较大的二极管会先导通。先导通的二极管导致电路电量发生变化，致使还没导通的二极管端电压有可能变换为反向偏置电压。

3.单相桥式整流电路分析

【例 6.3】 单相桥式整流电路如图6.8 所示。其输入电压 ui为正弦交流电，二极管均为理想元件，试分析整流电路波形图。

分析：因输入电压 u2为正弦交流电，则将电压分为正半周和负半周讨论4 个二极管的工作状态，即导通还是截止，从而分析出整流电路的波形图6.9。

解 （1） u2正半周。

因 u2﹥0，二极管D1、D3正偏导通，D2、D4反偏截止。其电流id1的通路如图6.8（a）所示。负载电阻RL上得到一个正半波电压uo。

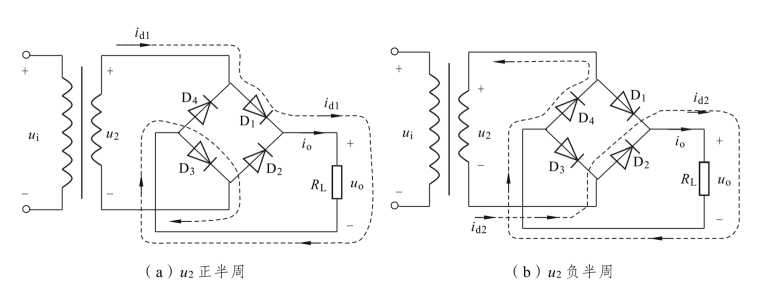
图6.8　例6.3图

（2） u2负半周。

因 u2﹤0，二极管D2、D4正偏导通，D1、D3反偏截止。其电流id2的通路如图6.8（b）所示。负载RL上得到另一个正半波电压uo。

解得：整流电路波形图如图6.9 所示。

结论：充分利用二极管的单向导电性，巧妙地用二极管构成桥式电路，从而实现将正弦交流电整流变换为脉动电流。