初态分析：电感元件的初始值计算方法

换路定则描述的是初始状态值的变化规律，即 uC（0+）=uC（0-）、iL（0+）=iL（0-），电路中其他电压、电流均不存在 u（0+）=u（0-）、i（0+）=i（0-）约束关系，因此，要根据t=0+瞬间的电路求得电压 u（0+）、电流i（0+），u（0+）、i（0+）称为初始值。

1.初始值求解步骤

1）计算初始状态值

画t=0-瞬时稳态电路图，计算 uC（0-）、iL（0-）；再根据换路定则 uC（0+）=uC（0-）、iL（0+）=iL（0-） 解得初始状态值。

注意：直流稳态电路中，电容C 用“开路”等效替代，电感L 用“短路线”等效替代。

2）画t=0+瞬时电路图

画t=0+瞬时电路的关键是将电容C、电感L 元件进行等效替代。

a）电容C

若 uC（0+） ≠0，则用直流电压源 uC（0+）来等效替代电容C，如图5.5（a）所示。

若 uC（0+）=0，则用“短路线”等效替代电容C。如图5.5（b）所示。

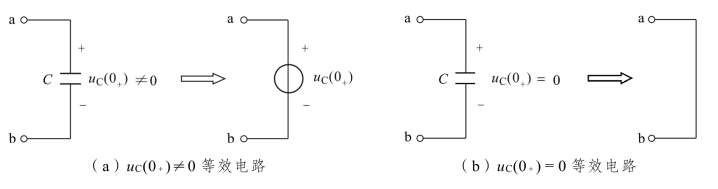
图5.5　电容元件的t＝0＋瞬时等效电路

b）电感L

若 iL（0+） ≠0，则用直流电流源 iL（0+）来等效替代电感L，如图5.6（a）所示。

若 iL（0+）=0，则用“开路”等效替代电感L。如图5.6（b）所示。

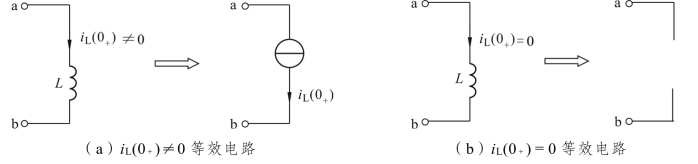
图5.6　电感元件的t＝0＋瞬时等效电路

c）计算初始值

根据t=0+瞬时电路图，计算电路的初始值电压 u（0+）和电流i（0+）。

2.初始值计算实例

【例5.3】 电路如图5.7（a）所示。t ﹤0时电路处于稳态，t=0时开关S 闭合。已知电阻 R1=10Ω，R2=R3=20Ω，电压源US=10V。试求电流 i1（0+）、i2（0+）及 iC（0+）。(www.xing528.com)

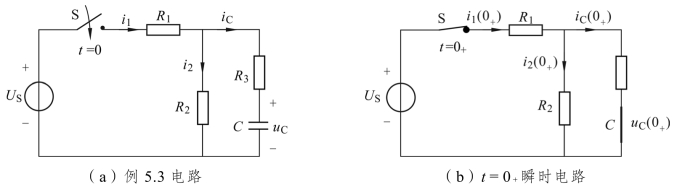
图5.7　例5.3 电路图

分析：

（1）首先计算初始状态值 uC（0+）。注意t=0-时，电路开关S 处于开路状态，电容等效为“开路”，uC（0-）=0 V。

（2） t=0+时，因 uC（0+）=0 V，用“短路”等效替代电容元件，如图（b）所示的t=0+瞬时等效电路。

解　初始状态值 uC（0+）

由图（b）解初始值 i1（0+）、i2（0+）及 iC（0+）

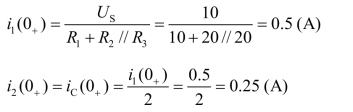
结论：在直流稳态电路中，当 uC（0+） ≠0 V 时，电容元件C 用“电压源”等效替代；当uC（0+）=0 V 时，电容元件C 用“短路”等效替代。另外，换路定则是针对电容上的电压定义的 uC（0+）=uC（0-），而电容元件中的初始值电流 iC（0+）不能根据 iC（0-）计算。

【例5.4】 电路如图5.8（a）所示。当t ﹤0时电路处于稳态，t=0时开关S 闭合。已知电感L=2 H，电阻 R1=R2=R3=10Ω，电压源US=30V。试求电流 i1（0+）、i2（0+）、iL（0+）及电压 uL（0+）。

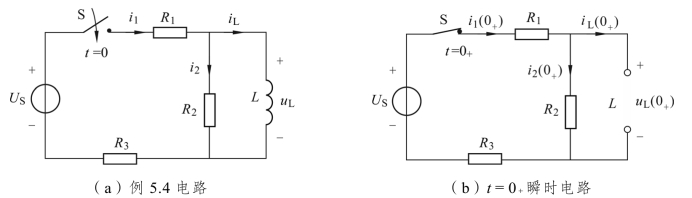
图5.8　例5.4 电路图

分析：

（1）计算初始状态值 iL（0+）；因换路前电路处于稳态，得 iL（0-）=0A。

（2）当t=0+时 iL（0+）=0A，电感元件用“开路”等效替代，如图（b）所示的t=0+瞬时等效电路。

解　初始状态值 iL（0+）

由图（b）电路解初始值 i1（0+）、i2（0+）及 uL（0+）

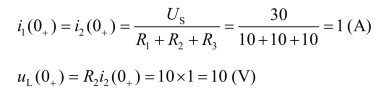
结论：在直流稳态电路中，当 iL（0+） ≠0 V 时，电感元件 L 用“电流源”等效替代；当iL（0+）=0 V 时，电感元件L 用“开路”等效替代。另外，换路定则是针对电感中的电流定义的 iL（0+）=iL（0-），而电感元件上的初始值电压 uL（0+）不能根据 uL（0-）计算。