电路与电子技术:使用三要素法的实例

【例5.7】 已知图5.13（a）所示电路中电容C=0.125 F，试分析当t≥0 时电路的电流 i1（t）、iC（t）和电压 uC（t），并画出电压 uC（t）的波形图。

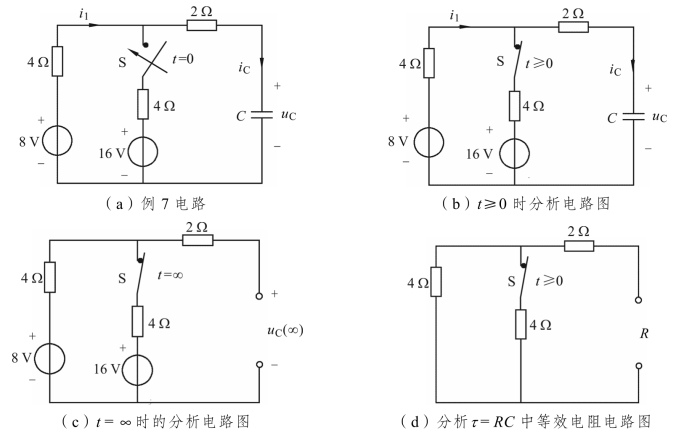
图5.13　例7 题解电路图

分析：

（1）根据换路定则解图（a）初始状态值 uC（0+）；根据换路后图（c）解得稳态值 uC（∞）；根据换路后图（d）解等效电阻R，由τ=RC得时间常数τ；由三要素式（5.7）解得电容电压 uC（t）。

（2）由元件C 的伏安特性解得电流 iC（t）。

（3）根据换路后图（b）解电流 i1（t）。

解：初始状态值

由图（c）解稳态值

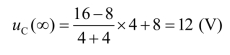
由图（d）解等效电阻R 值

则时间常数为

由三要素式（5.7）得

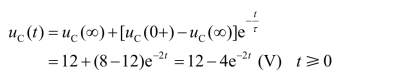
由元件C 伏安特性得

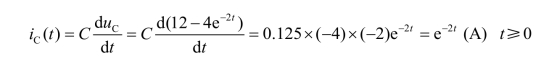
列图（b）的KVL 得

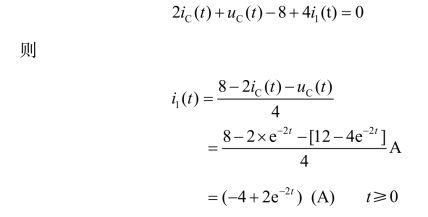
根据式uC（t）=（12-4e-2t）V t≥0，画时域波形图，如图5.14 所示。

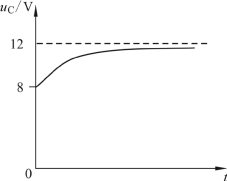
图5.14　电压uC（t）时域波形图

结论：“三要素法”是分析求解一阶时域电路方法中的一种。如果电路中没有严格要求必须用“三要素法”求解，则可灵活运用元件伏安特性、KCL、KVL、电路定理和分析方法进行分析计算。

【例5.8】 如图5.15（a）所示电路中，换路前电路已处于稳态，t=0时开关S 闭合，试求t≥0时电路中的 i1（t）和 uL（t）。

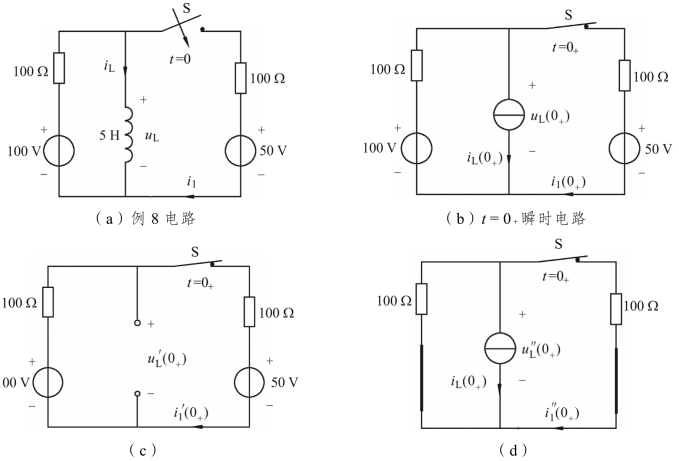
图5.15　例8 电路图(www.xing528.com)

分析：

（1）解图5.15（a）中电感电流 iL（0-），根据换路定则初始状态值 iL（0+）；画t＝0＋瞬时等效电路如图5.15（b）所示，用叠加定理解图5.15（c）（d）得初始值 uL（0+）、i1（0+）。

（2）画t=∞时等效电路，如图5.16（a）所示，解稳态值 uL（∞）、i1（∞）。

（3）由图5.16（b）计算等效电阻R，得时间常数τ。

（4）将三要素代入三要素式（5.7）。

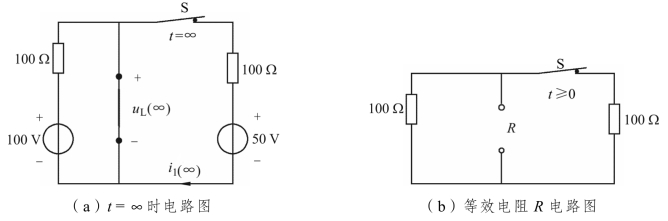
图5.16　稳态值及时间常数分析电路图

解：（1）求初始值。

由图5.15（a）求解初始状态值 iL（0+）：

由图5.15（c）解得

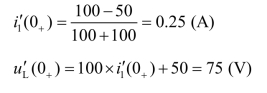
由图5.15（d）解得

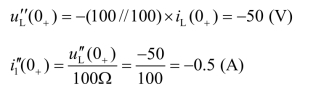
叠加得初始值：

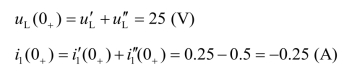
（2）求稳态值。

由图5.16（a）解得

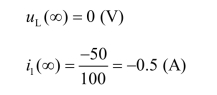
（3）求时间常数。

由图5.16（b）解得

则时间常数为

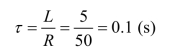
（4）由三要素法求解 i1（t）和 uL（t）。

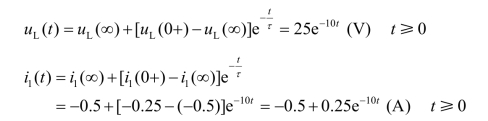
结论：“三要素法”是一阶电路的基本解题方法。即三要素的分析与计算，直接反映出对基础知识的掌握程度。