对称三相△形连接电路优化为：对称三相△形电路连接方案

1、对称△形负载电路

对称△形负载电路：当图4.4（b）中三相负载阻抗相同时，电路对称。如图4.8（a）所示，即 ZAB=ZBC=ZCA=Z，称电路为对称△形负载电路。

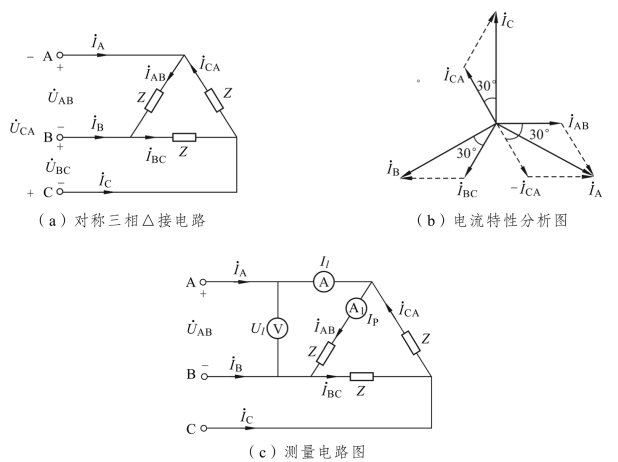
图4.8　△接电路及电流特性图

2.电压特性

图4.8（a）三相电路的线电压由三相电源决定，与三相负载大小无关。设图4.8（a）电压为

则△形连接对称电路电压特性为

（1）线电压等于对应的相电压（即对应阻抗上的相电压）；其测量电路如图4.8（c）所示。

（2）线电压有效值Ul等于相电压有效值Up，即Ul=UP。

3.电流特性

设图4.8（a）电路中负载阻抗为则电路的相电流为

如果设 φZ=0°，即

根据KCL，列图4.8（a）电路线电流方程，并将式（4.4）代入，得

式中，线电流与相电流之间的相量关系如图4.8（b）所示，其测量电路如图4.8（c）所示。则△形连接对称电路电流特性为

（1）相电流对称，线电流也对称。

（2）线电流有效值 Il是相电流有效值 IP的倍，即

（3）线电流相位滞后所对应的相电流的相位30°，即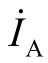滞后相位30°，滞后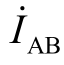相位30°，滞后相位30°。(www.xing528.com)

【例4.2】 对称三相电路如图4.9（a）所示。已知负载阻抗Z=（19.2+j14.4）Ω，传输线路阻抗 ZL=（3+j4）Ω，线电压UAB=380 V。试求负载端的线电压、线电流和负载中的相电流。

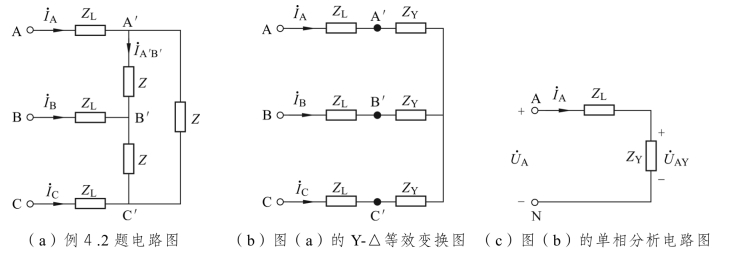
图4.9　例4.2图及分析计算电路图

分析：图4.9（a）所示三相对称负载Z 是△形连接，利用阻抗的Y-△等效变换，即将△形负载Z 等效变换为Y形连接，如图4.9（b）所示。再用单相电路[见图4.9（c）]分析计算△形连接的线电流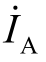。然后，再根据对称特性解得其他各参数。

解　图4.9（b）负载ZY为

设A 相电源电压为

由图4.9（c）得线电流

由三相电路的对称性得

根据线电流与相电线的特性，得

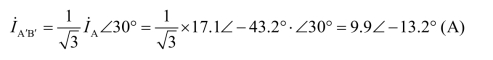
由对称性，得

负载端的线电压

由对称性，得

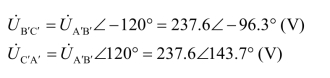
结论：对称三相△接电路分析中，常常应用等效变换，将△接等效变换为Y 接，再由单相分析电路计算△接的线电流。根据电压特性、电流特性和电路的对称性，推导出其他电量。