优化版：RLC并联谐振电路详解

1.并联谐振频率

电路如图3.56 所示。

图3.56 RLC 并联谐振电路

图3.56（a）电路的KCL 方程为

图3.56（b）等效导纳Y 为

谐振导纳Y 虚部为零时，即谐振角频率为

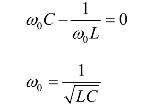
2.并联谐振特征

（1）电流导纳Y=G 最小；cosφ=1、电路呈阻性、u 与i 同相位；Q=0；iL与iC大小相等相位相反，如图3.56（c）所示。

（2）储能不为零。

电容中的电场能与电感中的磁场能相互转换。(www.xing528.com)

（3）品质因素。

谐振时，电感电流IL（或电容电流IC）与电流I 之比，称为RLC 并联谐振电路的品质因素，用Q 来表示，即

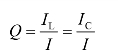
【例3.32】 电路如图3.57（a）所示，已知 iS（t）=sin tA，i2（t）=0A，L1=3 H，L2=8 H，R1=R2=R3=1Ω，试求C2、i1（t）、i3（t）、i4（t）。

图3.57 例3.38图

分析：

（1）将图（a）转换成相量电路图，如图（b）所示。

（2）分析图（b）得jXL1-jXC1=0，电路发生L1C1串联谐振；已知 i2（t）=0A，说明电路发生L2C2并联谐振。

（3）并联谐振可用“断路”等效替代；串联谐振可用“短路”等效替代，则图（b）电路可简化图（c），阻抗 ZAB=R1//R2。

解

结论：谐振往往发生于电路系统中的局部电路中，并联谐振、串联谐振可同时存在于同一个电路系统中。LC 并联电路如对外电路呈电流为零，则发生并联谐振，即可用“断路”等效替代；LC 串联电路如对外电路呈端电压为零，则发生串联谐振，即可用“短路”等效替代。